Напряженное и деформированное состояние - документ. Напряженно-деформированное состояние
Напряженно-деформированное состояние
(НДС) конструкции - совокупность внутренних напряжений и деформаций, возникающих при действии на неё внешних нагрузок, температурных полей и других факторов. НДС определяется расчётными и экспериментальными методами в виде распределения напряжений, деформаций и перемещений в конструкции и является основанием для оценки статической прочности и ресурса авиационных конструкций на всех этапах жизненного цикла летательного аппарата. При расчётах НДС определенным образом идеализируется расчётная схема (см.
Строительная механика, Конструктивно-силовая схема). С внедрением современных универсальных численных методов расчёта сложная авиационная конструкция может рассматриваться как совокупность простых механических элементов (балок, пластин, стержней и пр.). В одной из возможных схем расчёта НДС крыла малого удлинения стенки лонжеронов (л - л), стенки нервюр (н - н) и обшивка (о - о) моделируются плоскими четырёхугольными элементами, воспринимающими плоское напряжённое состояние, пояса лонжеронов и нервюр (п - п) моделируются стержнями. Различают общее и местное НДС. Общее НДС определяется в силовых элементах конструкции без учёта концентрации напряжений, вызванных местными конструктивно-технологическими особенностями (отверстиями, выточками и пр.). Местное НДС определяется вблизи концентратора напряжений с учётом вида концентратора и приложенной нагрузки. При расчётном методе исследования местного НДС вид нагрузки может быть определён из предшествующего расчёта общего НДС. Например, в расчётной схеме плоского кольцевого шпангоута к общему НДС относятся прогиб упругой линии шпангоута f и нормальное напряжение в наружном волокне верхнего пояса лонжерона ()0; к местному НДС - распределение напряжений (-)и по сечению С - С отверстия, расположенного в элементе шпангоута А - А, В - В.
В случае линейной упругости материала и малости перемещений (при линейном НДС) расчёт конструкции можно производить на единичные случаи нагружения. Например, НДС фюзеляжа рассчитывается отдельно при действии единичных значений силы p и изгибающего момента m, приложенных к оперению самолёта. НДС различных случаев совместного нагружения определяется сложением результатов расчётов НДС на единичные случаи нагружения с коэффициентами Kp и Km (суперпозиция результатов расчётов):
P = Kpp, M = Kmm.
При нелинейном НДС суперпозиция недопустима. Например, при расчёте несущей способности поперечного сечения фюзеляжа самолёта учитываются нелинейные эффекты - пластичность материала и потери устойчивости элементов конструкции. Результаты расчёта НДС должны подтверждаться экспериментально (см.
Тензометрия).
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Напряженное и деформированное состояние
напряженное деформированное состояние
Различают три вида напряженного состояния:
1) линейное напряженное состояние - растяжение (сжатие) в одном направлении;
2) плоское напряженное состояние - растяжение (сжатие) по двум направлениям;
3) объемное напряженное состояние - растяжение (сжатие) по трем взаимно перпендикулярным направлениям.
Рассматривают бесконечно малый параллелепипед (кубик). На его гранях могут быть нормальные и касательные напряжения. При изменении положения «кубика» напряжения меняются. Можно найти такое положение, при котором нет касательных напряжений см. рис.
Площадки, по которым не действуют касательные напряжения, называются главными площадками, а нормальные напряжения на этих площадках - главными напряжениями.
Главные напряжения обозначают
Разрежем элементарный параллелепипед (рис. а) наклонным сечением. Изображаем только одну плоскость. Рассматриваем элементарную треугольную призму (рис. б). Положение наклонной площадки определяется углом. Если поворот от оси x против час. стр. (см. рис. б), то >0.
: 1, 2, 3 и 1> 2> 3
Плоское напряженное состояние
Нормальные напряжения имеют индекс, соответствующий оси их направления. Касательные напряжения, обычно, имеют два индекса: первый соответствует направлению нормали к площадке, второй - направлению самого напряжения (к сожалению, встречаются и другие обозначения, и другой выбор осей координат, что приводит к изменению знаков в некоторых формулах).
Нормальное напряжение положительно, если оно растягивающее, касательное напряжение положительно, если оно стремится повернуть рассматриваемую часть элемента относительно внутренней точки по час. стр (для касательного напряжения в некоторых учебниках и вузах принято обратное).
Напряжения на наклонной площадке:
Закон парности касательных напряжений: если по площадке действует касательное напряжение, то по перпендикулярной к ней площадке будет действовать касательное напряжение, равное по величине и противоположное по знаку. (xz= - zx)
В теории напряженного состояния различают две основные задачи.
Прямая задача. По известным главным напряжениям: 1= max, 2= min требуется определить для площадки, наклоненной под заданным углом () к главным площадкам, нормальные и касательные напряжения:
Для перпендикулярной площадки:
Откуда видно, что +=1+2 - сумма нормальных напряжений по двум взаимно перпендикулярным площадкам инварианта (независима) по отношению к наклону этих площадок.
Как и в линейном напряженном состоянии максимальные касательные напряжения имеют место при =45о, т. е. по площадкам, наклоненным к главным площадкам под углом 45о
Обратная задача. По известным нормальным и касательным напряжениям, действующим в двух взаимно перпендикулярных площадках, найти главные (max и min) напряжения и положение главных площадок.
(касательные напряжения по главным площадкам равны 0).
Угол 0, определяющий положение главных площадок:
Если одно из главных напряжений окажется отрицательным, то их надо обозначать 1, 3, если оба отрицательны, то 2, 3.
Объемное напряженное состояние
Напряжения в любой площадке при известных главных напряжениях 1, 2, 3:
где 1, 2, 3 - углы между нормалью к рассматриваемой площадке и направлениями главных напряжений.
Наибольшее касательное напряжение:
Оно действует по площадке параллельной главному напряжению 2 и наклоненной под углом 45о к главным напряжениям 1 и 3.
Круг Мора для объемного напряженного состояния.
Точки, являющиеся вершинами кругов соответствуют диагональным площадкам, наклоненным под 45о к главным напряжениям:
(иногда называют главными касательными напряжениями).
Плоское напряженное состояние - частный случай объемного и тоже может быть представлено тремя кругами Мора, при этом одно из главных напряжений должно быть равно 0. Для касательных напряжений также, как и при плоском напряженном состоянии, действует закон парности: составляющие касательных напряжений по взаимно перпендикулярным площадкам, перпендикулярные к линии пересечения этих площадок, равны по величине и обратны по направлению.
Напряжения по октаэдрической площадке.
Октаэдрическая площадка (АВС) - площадка, равнонаклоненная ко всем главным направлениям.
Октаэдрическое нормальное напряжение равно среднему из трех главных напряжений.
Октаэдрическое касательное напряжение пропорционально геометрической сумме главных касательных напряжений. Интенсивность напряжений:
x+y+z=1+2+3 - сумма нормальных напряжений, действующих по любым трем взаимно перпендикулярным площадкам есть постоянная величина, равная сумме главных напряжений (первый инвариант).
Деформации при объемном напряженном состоянии.
Обобщенный закон Гука (закон Гука при объемном напряжении) :
Относительная объемная деформация:
Изменение объема не зависит от соотношения между главными напряжениями, а зависит от суммы главных напряжений. Т. е. элементарный кубик получит такое же изменение объема, если к его граням будут приложены одинаковые средние напряжения: , тогда, где К= - модуль объемной деформации. При деформации тела, материал которого имеет коэффициент Пуассона = 0, 5 (например, резина) объем тела не меняется.
Потенциальная энергия деформации
При простом растяжении (сжатии) потенциальная энергия U=.
Удельная потенциальная энергия - количество потенциальной энергии, накапливаемое в единице объема: u = ; . В общем случае объемного напряженного состояния, когда действуют три главных напряжения:
Полная энергия деформации, накапливаемая в единице объема, может рассматриваться как состоящая из двух частей: 1) энергии uo, накапливаемой за счет изменения объема (т. е. одинакового изменения всех размеров кубика без изменения кубической формы) и 2) энергии uф, связанной с изменением формы кубика (т. е. энергии, расходуемой на превращение кубика в параллелепипед). u = uо + uф.
Тензор напряжений (матрица третьего порядка).
При переходе к главным напряжениям тензор напряжений получает вид:
При повороте системы координат коэффициенты тензора меняются, сам тензор остается постоянным.
Аналогичные зависимости возникают при рассмотрении деформированного состояния в точке. Сопоставление зависимостей напряженного и деформированного плоского состояния (аналогия) :
Относительная деформация, - угол сдвига.
Та же аналогия сохраняется и для объемного состояния. Поэтому имеем инварианты деформированного состояния:
J2= xy +yz + zx - 2xy - 2yz - 2zx;
Тензор деформаций.
x, y, z, xy, yz, zx - компоненты деформированного состояния.
Для осей, совпадающих с направлениями главных деформаций 1, 2, 3, тензор деформаций принимает вид: .
Теории прочности
В общем случае опасное напряженное состояние элемента конструкции зависит от соотношения между тремя главными напряжениями (1, 2, 3). Т. е., строго говоря, для каждого соотношения нужно экспериментально определять величину предельного напряжения, что нереально. Поэтому были приняты такие методы расчета прочности, которые позволяли бы оценить степень опасности любого напряженного состояния по напряжению растяжения - сжатия. Они называются теориями прочности (теории предельных напряженных состояний).
1-ая теория прочности (теория наибольших нормальных напряжений) : причиной наступления предельного напряженного состояния являются наибольшие нормальные напряжения. max= 1 . Главный недостаток: не учитываются два других главных напряжения. Подтверждается опытом только при растяжении весьма хрупких материалов (стекло, гипс). В настоящее время практически не применяется.
2-ая теория прочности (теория наибольших относительных деформаций) : причиной наступления предельного напряженного состояния являются наибольшие удлинения. max= 1 . Учитывая, что 1=, - коэффициент Пуассона, получаем условие прочности эквII= 1 - (2 + 3) . экв - эквивалентное (расчетное) напряжение. В настоящее время теория используется редко, только для хрупких материалов (бетон, камень).
3-я теория прочности (теория наибольших касательных напряжений) : причиной наступления предельного напряженного состояния являются наибольшие касательные напряжения max , max=, условие прочности: эквIII= 1 - 3 . Основной недостаток - не учитывает влияние 2.
При плоском напряженном состоянии: эквIII= . При y=0 получаем Широко используется для пластичных материалов.
4-я теория прочности (энергетическая теория) : причиной наступления предельного напряженного состояния являются величина удельной потенциальной энергии изменения формы. uф. .
Учитывает, все три главных напряжения. При плоском напряженном состоянии: . При y=0,
Широко используется для пластичных материалов.
Теория прочности Мора Получена на основе кругов напряжений Мора.
Используется при расчетах хрупких материалов, у которых допускаемые напряжения на растяжение [p] и сжатие [с] не одинаковы (чугун).
Для пластичных материалов [p]=[с] теория Мора превращается в 3-ю теорию.
Круг Мора (круг напряжений). Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Откладываем от оси из центра С луч под углом 2 (>0, то против час. стр.), находим точку D,
координаты которой: , . Можно графически решать как прямую, так и обратную задачи.
Чистый сдвиг
Чистый сдвиг - напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения, где Q - сила, действующая вдоль грани, F - площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них - наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т. е. это частный случай плоского напряженного состояния, при котором главные напряжения: 1= - 3 = ; 2= 0. Главные площадки составляют с площадками чистого сдвига угол 45о.
При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. - абсолютный сдвиг,
Относительный сдвиг или угол сдвига.
Закон Гука при сдвиге: = /G или = G.
G - модуль сдвига или модуль упругости второго рода [МПа] - постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е - модуль упругости, - коэффициент Пуассона).
Потенциальная энергия при сдвиге:
Удельная потенциальная энергия деформации при сдвиге:
где V=аF - объем элемента. Учитывая закон Гука, .
Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.
Круг Мора при чистом сдвиге.
Кручение
Такой вид деформации, при котором в поперечных сечениях возникает только одни крутящие моменты - Мк. Знак крутящего момента Мк удобно определять по направлению внешнего момента. Если при взгляде со стороны сечения внешний момент направлен против час. стр., то Мк>0 (встречается и обратное правило). При кручении происходит поворот одного сечения относительно другого на угол закручивания -. При кручении круглого бруса (вала) возникает напряженное состояние чистого сдвига (нормальные напряжения отсутствуют), возникают только касательные напряжения. Принимается, что сечения плоские до закручивания остаются плоскими и после закручивания - закон плоских сечений. Касательные напряжения в точках сечения изменяются пропорционально расстоянию точек от оси. Из закона Гука при сдвиге: =G, G - модуль сдвига, - полярный момент сопротивления круглого сечения. Касательные напряжения в центре равны нулю, чем дальше от центра, тем они больше. Угол закручивания, GJp - жесткость сечения при кручении. - относительный угол закручивания. Потенциальная энергия при кручении: . Условие прочности: , =, для пластичного материала за пред принимается предел текучести при сдвиге т, для хрупкого материала - в - предел прочности, [n] - коэффициент запаса прочности. Условие жесткости при кручении: max - допустимый угол закручивания.
Кручение бруса прямоугольного сечения
При этом нарушается закон плоских сечений, сечения некруглой формы при кручении искривляются - депланация поперечного сечения.
Эпюры касательных напряжений прямоугольного сечения.
; , Jk и Wk - условно называют моментом инерции и моментом сопротивления при кручении. Wk= hb2,
Jk= hb3, Максимальные касательные напряжения max будут посредине длинной стороны, напряжения по середине короткой стороны: = max, коэффициенты: , приводятся в справочниках в зависимости от отношения h/b (например, при h/b=2, =0, 246; =0, 229; =0, 795.
Изгиб
Плоский (прямой) изгиб - когда изгибающий момент действует в плоскости, проходящей через одну из главных центральных осей инерции сечения, т. е. все силы лежат в плоскости симметрии балки. Основные гипотезы (допущения) : гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения - сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются.
Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: , - радиус кривизны нейтрального слоя, y - расстояние от некоторого волокна до нейтрального слоя. Закон Гука при изгибе: , откуда (формула Навье) : , Jx - момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента, EJx - жесткость при изгибе, - кривизна нейтрального слоя.
Максимальные напряжения при изгибе возникают в точках, наиболее удаленных от нейтрального слоя: , Jx/ymax=Wx-момент сопротивления сечения при изгибе, .
Если сечение не имеет горизонтальной оси симметрии, то эпюра нормальных напряжений не будет симметричной. Нейтральная ось сечения проходит через центр тяжести сечения. Формулы для определения нормального напряжения для чистого изгиба приближенно годятся и когда Q0. Это случай поперечного изгиба. При поперечном изгибе, кроме изгибающего момента М, действует поперечная сила Q и в сечении возникают не только нормальные, но и касательные напряжения. Касательные напряжения определяются формулой Журавского: , где Sx (y) - статический момент относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии «y» от нейтральной оси; Jx - момент инерции всего поперечного сечения относительно нейтральной оси, b (y) - ширина сечения в слое, на котором определяются касательные напряжения.
Для прямоугольного сечения:
для круглого сечения:
для сечения любой формы
k- коэфф., зависящий от формы сечения (прямоугольник: k= 1, 5; круг - k= 1, 33).
Mmax и Qmax определяются из эпюр изгибающих моментов и поперечных сил. Для этого балка разрезается на две части и рассматривается одна из них.
Действие отброшенной части заменяется внутренними силовыми факторами М и Q, которые определяются из уравнений равновесия. В некоторых вузах момент М>0 откладывается вниз, т. е. эпюра моментов строится на растянутых волокнах. При Q= 0 имеем экстремум эпюры моментов. Дифференциальные зависимости между М, Q и q:
q - интенсивность распределенной нагрузки [кН/м]
Главные напряжения при поперечном изгибе:
Расчет на прочность при изгибе: два условия прочности, относящиеся к различным точкам балки: а) по нормальным напряжениям, (точки наиболее удаленные от С) ; б) по касательным напряжениям, (точки на нейтр. оси). Из а) определяют размеры балки: , которые проверяют по б). В сечениях балок могут быть точки, где одновременно большие нормальные и большие касательные напряжения. Для этих точек находятся эквивалентные напряжения, которые не должны превышать допустимых. Условия прочности проверяются по различным теориям прочности
I-я: ; II-я: (при коэфф. Пуассона =0, 3) ; - применяются редко.
III-я: , IV-я: ,
теория Мора: , (используется для чугуна, у которого допускаемое напряжение на растяжение [р][с] - на сжатие).
Определение перемещений в балках при изгибе
Имеем закон Гука при изгибе: , где (х) - радиус кривизны изогнутой оси балки в сечении х, М (х) - изгибающий момент в том же сечении, EJ - жесткость балки. Из высшей математики известно: - дифференциальное уравнение изогнутой оси балки. - тангенс угла между осью х и касательной к изогнутой оси. Эта величина очень мала (прогибы балки малы) ее квадратом пренебрегают и угол поворота сечения приравнивают тангенсу. Приближенное дифференциальное ур-ние изогнутой оси балки: . Если ось y направлена вверх, то знак (+). В некоторых вузах ось y направляется вниз (-). Интегрируя дифф. уравнение, получаем: - ур-ние углов поворота, интегрируем второй раз: - получаем ур-ние прогибов. Постоянные интегрирования С и D находятся из граничных условий, которые зависят от способов закрепления балки.
Метод начальных параметров. Начало координат выбирают в крайней левой точке. При включении в уравнение момента М, который приложен на расстоянии «а» от начала координат, его умножают на множитель (х - а) 0, который равен 1. Любую распределенную нагрузку продлевают до конца балки, а для ее компенсации прикладывают нагрузку обратного направления.
Для рис. :
EJ= M (x) = RAx - - M (x - a) 0 + - P (x - a - b) ; интегрируем:
EJ = EJ0 + RA - - M (x - a) + - P;
EJy =EJy0 + EJ0x + RA - - M + - P.
Начальные параметры - то, что мы имеем в начале координат, т. е. для рис. : М0=0, Q0=RA, прогиб y0=0, угол поворота 00. 0 находим из подстановки во второе уравнение условия закрепления правой опоры: x=a+b+c; y (x) =0.
Дифференциальные зависимости при изгибе:
Определение перемещений способом фиктивной нагрузки. Сопоставляя уравнения:
имеем аналогию, определение прогибов можно свести к определению моментов от некоторой фиктивной (условной) нагрузки в фиктивной балке: . Момент от фиктивной нагрузки Мф после деления на EJ равен прогибу «y» в заданной балке от заданной нагрузки. Учитывая, что и, получаем, что угол поворота в заданной балке численно равен фиктивной поперечной силе в фиктивной балке. , . При этом должна быть полная аналогия в граничных условиях двух балок. Каждой заданной балке соответствует своя фиктивная балка.
Закрепление фиктивных балок выбирается из того условия, чтобы на концах балки и на опорах имелось полное соответствие между «y» и «« в заданной балке и Мф и Qф в фиктивной балке. Если эпюры моментов как в действительной, так и в фиктивной балках строить со стороны растянутого волокна (т. е. положительный момент откладывать вниз), то линии прогибов в заданной балке совпадает с эпюрой моментов в фиктивной балке.
Статически неопределимые балки.
Статически неопределимыми называются системы, реакции в которых не могут быть определены из уравнений равновесия твердого тела. В таких системах больше связей, чем это необходимо для равновесия. Степень статической неопределимости балки (не имеющей промежуточных шарниров - неразрезные балки) равна избыточному (лишнему) числу внешних связей (более трех).
Раскрытие статической неопределимости с помощью дифф-ного урав-ния изогнутой оси балки. Записываем дифф-ное урав-ние куда входит в качестве неизвестной реакция RB и дважды его интегрируем:
EJ= RВx - ; EJ = RВ - + С;
EJy = RВ - + Сх + D. Используем условия закрепления балки: х=0, y=0, =0; x=L, y=0. Подставляем их в два последних уравнения, находи постоянные интегрирования С и D и неизвестную реакцию RB. Далее из урав-ний статики: HA=0; RA - qL + RB=0; RBL - + MA=0; находятся RA и MA.
Уравнение совместности перемещений. Статически определимая балка, которая получается из статически неопределимой при удалении «лишнего» закрепления, называется основной системой. За «лишнюю» неизвестную можно взять любую из реакций. Приложив к основной системе заданные нагрузки добавляем условие, которое обеспечивает совпадение заданной балки и основной - уравнение совместности перемещений. Для рис. : yB=0, т. е. прогиб в точке В = 0. Решение этого уравнения возможно разными способами.
Способ сравнения перемещений. Определяется прогиб точки В (рис.) в основной системе под действием заданной нагрузки (q) : yВq=. Далее рассматривается основная система под действием «лишней» неизвестной RB, и находится прогиб от действия RB: . Подставляем в уравнение совместности перемещений: yB= yВq += 0, т. е. += 0, откуда RB=, далее остальные реакции находятся из уравнений статики.
Теорема о трех моментах. Используется при расчете неразрезных балок - балок на многих опорах, одна из которых неподвижна, остальные подвижны. Для перехода от статически неопределимой балки к статически определимой основной системе над -лишними опорами вставляются шарниры. Лишними неизвестные: моменты Mn, приложенные к концам пролетов над лишними опорами.
Строятся эпюры моментов для каждого пролета балки от заданной нагрузки, рассматривая каждый пролет, как простую балку на двух опорах. Для каждой промежуточной опоры «n» составляется уравнение трех моментов:
n, n+1-площади эпюр, an - расстояние от центра тяжести левой эпюры до левой опоры, bn+1 - расстояние от центра тяжести правой эпюры до правой опоры. Число уравнений моментов равно числу промежуточных опор. Совместное их решение позволяет найти неизвестные опорные моменты. Зная опорные моменты, рассматриваются отдельные пролеты и из уравнений статики находятся неизвестные опорные реакции. Если пролета всего два, то левый и правый моменты известны, т. к. это либо заданные моменты, либо они равны нулю. В результате получаем одно уравнение с одним неизвестным М1.
Общие методы определения перемещений
Работа постоянных сил: А=РР, Р - обобщенная сила - любая нагрузка (сосредоточенная сила, сосредоточенный момент, распределенная нагрузка), Р - обобщенное перемещение (прогиб, угол поворота). Обозначение mn означает перемещение по направлению обобщенной силы «m», которое вызвано действием силы обобщенной «n». Полное перемещение, вызванное несколькими силовыми факторами: Р=РP+РQ+РM. Перемещения вызванные единичной силой или единичным моментом: - удельное перемещение. Если единичная сила Р=1 вызвала перемещение Р, то полное перемещение вызванное силой Р, будет: Р=РР. Если силовые факторы, действующие на систему, обозначить Х1, Х2, Х3 и т. д., то перемещение по направлению каждого из них:
где Х111=+11; Х212=+12; Хimi=+mi. Размерность удельных перемещений: , Дж- джоули размерность работы 1Дж = 1Нм.
Работа внешних сил, дейст-щих на упругую систему:
Действительная работа при статическом действии обобщенной силы на упругую систему равна половине произведения окончательного значения силы на окончательное значение соответствующего перемещения. Работа внутренних сил (сил упругости) в случае плоского изгиба:
k - коэффициент, учитывающий неравномерность распределения касательных напряжений по площади поперечного сечения, зависит от формы сечения.
На основании закона сохранения энергии: потенциальная энергия U=A.
Теорема о взаимности работ (теорема Бетли). Два состояния упругой ситемы:
11- перемещение по направл. силы Р1 от действия силы Р1;
12- перемещение по направл. силы Р1 от действия силы Р2;
21- перемещение по направл. силы Р2 от действия силы Р1;
22- перемещение по направл. силы Р2 от действия силы Р2.
А12=Р112 - работа силы Р1 первого состояния на перемещении по ее направлению, вызванном силой Р2 второго состояния. Аналогично: А21=Р221 - работа силы Р2 второго состояния на перемещении по ее направлению, вызванном силой Р1 первого состояния. А12=А21. Такой же результат получается при любом числе сил и моментов. Теорема о взаимности работ: Р112=Р221.
Работа сил первого состояния на перемещениях по их направлениям, вызванных силами второго состояния, равна работе сил второго состояния на перемещениях по их направлениям, вызванных силами первого состояния.
Теорема о взаимности перемещений (теорема Максвелла) Если Р1=1 и Р2=1, то Р112=Р221, т. е. 12=21, в общем случае mn=nm.
Для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй единичной силы, вызванному первой силой.
Универсальный метод определения перемещений (линейных и углов поворота) - метод Мора. К системе прикладывают единичную обобщенную силу в точке, для которой ищется обобщенное перемещение. Если определяется прогиб, то единичная сила представляет собой безразмерную сосредоточенную силу, если определяется угол поворота, то - безразмерный единичный момент. В случае пространственной системы действуют шесть компонентов внутренних усилий. Обобщенное перемещение определяется формулой (формула или интеграл Мора) :
Черта над М, Q и N указывает на то, что эти внутренние усилия вызваны действием единичной силы. Для вычисления входящих в формулу интегралов надо перемножить эпюры соответствующих усилий. Порядок определения перемещения: 1) для заданной (действительной или грузовой) системы находят выражения Mn, Nn и Qn; 2) по направлению искомого перемещения прикладывают соответствующую ему единичную силу (силу или момент) ; 3) определяют усилия от действия единичной силы; 4) найденные выражения подставляют в интеграл Мора и интегрируют по заданным участкам. Если полученное mn>0, то перемещение совпадает с выбранным направлением единичной силы, если <0, то противоположно.
Для плоской конструкции:
Обычно при определении перемещений пренебрегают влиянием продольных деформаций и сдвигом, которые вызываются продольной N и поперечной Q силами, учитываются только перемещения, вызываемые изгибом. Для плоской системы будет:
Вычисление интеграла Мора способом Верещагина. Интеграл для случая, когда эпюра от заданной нагрузки имеет произвольное очертание, а от единичной - прямолинейное удобно определять графо-аналитическим способом, предложенным Верещагиным. , где - площадь эпюры Мр от внешней нагрузки, yc- ордината эпюры от единичной нагрузки под центром тяжести эпюры Мр. Результат перемножения эпюр равен произведению площади одной из эпюр на ординату другой эпюры, взятой под центром тяжести площади первой эпюры. Ордината должна быть обязательно взята из прямолинейной эпюры. Если обе эпюры прямолинейны, то ординату можно взять из любой.
Перемещение: . Вычисление по этой формуле производится по участкам, на каждом из которых прямолинейная эпюра должна быть без переломов. Сложную эпюру Мр разбивают на простые геометрические фигуры, для которых легче определить координаты центров тяжести. При перемножении двух эпюр, имеющих вид трапеций, удобно использовать формулу: . Эта же формула годится и для треугольных эпюр, если подставить соответствующую ординату = 0.
При действии равномерно распределенной нагрузки на шарнирно опертую балку эпюра строится в виде выпуклой квадратичной параболы, площадь которой (для рис. , т. е. , хС=L/2).
Для «глухой» заделки при равномерно распределенной нагрузке имеем вогнутую квадратичную параболу, для которой; , хС=3L/4. Тоже можно получить, если эпюру представить разностью площади треугольника и площади выпуклой квадратичной параболы: . «Отсутствующая» площадь считается отрицательной.
Теорема Кастильяно. - перемещение точки приложения обобщенной силы по направлению ее действия равно частной производной от потенциальной энергии по этой силе. Пренебрегая влиянием на перемещение осевых и поперечных сил, имеем потенциальную энергию: , откуда.
Статически неопределимые системы
Статически неопределимые системы - системы, силовые факторы в элементах которых не могут быть определены только из уравнений равновесия твердого тела. В таких системах число связей больше, чем необходимо для равновесия. Степень статической неопределимости: S = 3n - m, n - число замкнутых контуров в конструкции, m - число одиночных шарниров (шарнир, соединяющий два стержня, считается за один, соединяющий три стержня - за два и т. д.). Метод сил - в качестве неизвестных принимают силовые факторы. Последовательность расчета: 1) устанавливают степень статич. неопределимости; 2) путем удаления лишних связей заменяют исходную систему статически определимой - основной системой (таких систем может быть несколько, но при удалении лишних связей не должна нарушаться геометрическая неизменяемость конструкции) ; 3) основную систему загружают заданными силами и лишними неизвестными; 4) неизвестные усилия должны быть подобраны так, чтобы деформации исходной и основной систем не отличались. Т. е. реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям = 0. Канонические уравнения метода сил:
Эти уравнения являются дополнительными ур-ями деформаций, которые позволяют раскрыть статич. неопределимость. Число ур-ий = числу отброшенных связей, т. е. степени неопределимости системы.
ik - перемещение по направлению i, вызванное единичной силой действующей по направлению k. ii - главные, ik - побочные перемещения. По теореме о взаимности перемещений: ik=ki. ip- перемещение по направлению связи i, вызванное действием заданной нагрузки (грузовые члены). Перемещения, входящие в канонические уравнения удобно определять по методу Мора.
Для этого к основной системе прикладывают единичные нагрузки Х1=1, Х2=1, Хn=1, внешнюю нагрузку и строят эпюры изгибающих моментов. По интегралу Мора находят:
Черта над М указывает на то, что эти внутренние усилия вызваны действием единичной силы.
Для систем, состоящих из прямолинейных элементов перемножение эпюр удобно производить по способу Верещагина. ; и т. д. Р - площадь эпюры Мр от внешней нагрузки, yСр- ордината эпюры от единичной нагрузки под центром тяжести эпюры Мр, 1 - площадь эпюры М1 от единичной нагрузки. Результат перемножения эпюр равен произведению площади одной из эпюр на ординату другой эпюры, взятой под центром тяжести площади первой эпюры.
Расчет плоских кривых брусьев (стержней )
К кривым брусьям относятся крюки, звенья цепей, арки и т. п. Ограничения: поперечное сечение имеет ось симметрии, ось бруса плоская кривая, нагрузка действует в той же плоскости. Различают брусья малой кривизны: h/R<1/5, большой кривизны: h/R1/5. При изгибе брусьев малой кривизны нормальные напряжения рассчитывают по формуле Навье, как для балок с прямой осью: . При чистом изгибе брусьев большой кривизны: ,
rН- радиус нейтрального слоя, е=R - rН, R - радиус слоя, в котором расположены центры тяжести сечения. Нейтральная ось кривого бруса не проходит через центр тяжести сечения С. Она всегда расположена ближе к центру кривизны, чем центр тяжести сечения. , =rН - y. Зная радиус нейтрального слоя можно определить расстояние «е» от нейтрального слоя до центра тяжести. Для прямоугольного сечения высотой h, с наружным радиусом R2 и внутренним R1: ; для разных сечений формулы приведены в справочной лит-ре. При h/R<1/2 независимо от формы сечения можно определять «е» по приближенной формуле: , где Jx - момент инерции сечения относительно оси, проходящей через его центр тяжести перпендикулярно плоскости кривизны бруса.
Нормальные напряжения в сечении распределяются по гиперболическому закону (у наружного края сечения меньше, у внутреннего больше). При действии еще и нормальной силы N: (здесь rН - радиус нейтрального слоя, который был бы при действии только момента М, т. е. при N=0, но в действительности при наличии продольной силы этот слой уже не является нейтральным). Условие прочности: , при этом рассматриваются крайние точки, в которых суммарные напряжения от изгиба и растяжения-сжатия будут наибольшие, т. е. y= - h2 или y= h1. Перемещения удобно определять методом Мора.
Устойчивость сжатых стержней . Продольный изгиб
Разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит заданной формы. Например, изгиб при продольном сжатии тонкой линейки. Потеря устойчивости прямолинейной формы равновесия центрально сжатого стержня называется продольным изгибом. Упругое равновесие устойчиво, если деформированное тело при любом малом отклонении от состояния равновесия стремится вернуться к первоначальному состоянию и возвращается к нему при удалении внешнего воздействия. Нагрузка, превышение которой вызывает потерю устойчивости, называется критической нагрузкой Ркр (критической силой). Допускаема нагрузка [P]=Pкр/nу, nу - нормативный коэффициент запаса устойчивости. Приближенное дифференциальное ур-ние упругой линии: , Е -модуль упругости материала стержня, М - изгибающий момент, Jmin- наименьший момент инерции сечения стержня. При потере устойчивости прогиб, как правило, происходит перпендикулярно к оси наименьшей жесткости, относительно которой - J=Jmin. Рассматривается приближенное дифф-ное ур-ие, т. к. потеря устойчивости возникает при малых деформациях. M=-Py, получаем однородное дифф-ное уравнение: , где. Решая дифф-ное ур-ие находим наименьшее значение критической силы - формула Эйлера: - формула дает значение критической силы для стержня с шарнирно закрепленными концами. При различных закреплениях: , - коэффициент приведения длины.
При шарнирном закреплении обоих концов стержня =1; для стержня с заделанными концами =0, 5; для стержня с одним заделанным и другим свободным концом =2; для стержня с одним заделанным и другим шарнирно закрепленным концом =0, 7.
Критическое сжимающее напр-ние. : , - гибкость стержня, - наименьший главный радиус инерции площади сечения стержня. Эти формулы справедливы только тогда, когда напряжения крпц- предел пропорциональности, т. е. в пределах применимости закона Гука. Формула Эйлера применима при гибкости стержня: , например, для стали Ст3 (С235) кр»100. Для случая <кр критическое напряжение вычисляется по эмпирической (полученной экспериментально) формуле Ясинского: кр= a - b, коэффициенты «a» и «b» в справочной лит-ре (Ст3: a=310МПа; b=1, 14МПа).
Достаточно короткие стержни, для которых <0=40 (для сталей) назыв-тся стержни малой гибкости. Такие стержни рассчитывают только на прочность, т. е. принимают кр=т (предел текучести) - для пластичных материалов и кр=В (временное сопротивление) - для хрупких материалов. При расчете стержней большой гибкости используют условие устойчивости: , Fбрутто- полная площадь сечения,
(Fнетто=Fбрутто-Fослабл -площадь ослабленного сечения с учетом площади отверстий в сечении Fослабл, например, от заклепок). [у]=кр/nу, nу- нормативный коэф. запаса устойчивости. Допускаемое напряжение [у] выражается через основное допускаемое напряжение , используемое при расчетах на прочность: [у]=, - коэффициент уменьшения допускаемого напряжения для сжатых стержней (коэффициент продольного изгиба). Значения приведены в табл. в учебниках и зависят от материала стержня и его гибкости (например, для стали Ст3 при =120 =0, 45).
При проектировочном расчете требуемой площади сечения на первом шаге принимают 1=0, 5-0, 6; находят: . Далее зная Fбрутто, подбирают сечение, определяют Jmin, imin и, устанавливают по табл. фактическое 1I, если оно существенно отличается от 1, расчет повторяется при среднем 2= (1+1I) /2. В результате второй попытки находят 2I, сравнивают с предыдущем значением и т. д., пока не достигнуто достаточно близкое совпадение. Обычно требуется 2-3 попытки.
Геометрические характеристики плоских сечений
Площадь: , dF - элементарная площадка.
Статический момент элемента площади dF относительно оси 0x - произведение элемента площади на расстояние «y» от оси 0x: dSx = ydF
Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и x:
; [см3, м3, т. д. ].
Координаты центра тяжести: . Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями Fi и координатами центров тяжести xi, yi. Статический момент площади всей фигуры = сумме статических моментов каждой ее части:
Координаты центра тяжести сложной фигуры:
Моменты инерции сечения
Осевой (экваториальный) момент инерции сечения - сумма произведений элементарных площадок dF на квадраты их расстояний до оси.
; [см4, м4, т. д. ].
Полярный момент инерции сечения относительно некоторой точки (полюса) - сумма произведений элементарных площадок на квадраты их расстояний от этой точки. ; [см4, м4, т. д. ]. Jy + Jx = Jp.
Центробежный момент инерции сечения - сумма произведений элементарных площадок на их расстояния от двух взаимно перпендикулярных осей. .
Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с осями симметрии, равен нулю.
Осевые и полярные моменты инерции всегда положительны, центробежные моменты инерции могут быть положительными, отрицательными или равными нулю.
Момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.
Моменты инерции сечений простой формы
Прямоугольное сечение Круг
Треугольник
равнобедренный
Прямоугольный
Треугольник
Четверть круга
на рис. (-)
Полукруг
Моменты инерции стандартных профилей находятся из таблиц сортамента:
Двутавр Швеллер Уголок
Моменты инерции относительно параллельных осей:
момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. Jy1x1=Jyx + abF; («a» и «b» подставляют в формулу с учетом их знака).
Зависимость между моментами инерции при повороте осей:
Jx1=Jxcos2 + Jysin2 - Jxysin2; Jy1=Jycos2 + Jxsin2 + Jxysin2;
Jx1y1= (Jx - Jy) sin2 + Jxycos2;
Угол >0, если переход от старой системы координат к новой происходит против час. стр. Jy1 + Jx1= Jy + Jx
Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т. е. главные оси инерции - оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: , если 0>0 оси поворачиваются против час. стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:
Jmax + Jmin= Jx + Jy. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:
Jx1=Jmaxcos2 + Jminsin2; Jy1=Jmaxcos2 + Jminsin2; Jx1y1= (Jmax - Jmin) sin2;
Конечной целью вычисления геометрических характеристик сечения является определение главных центральных моментов инерции и положения главных центральных осей инерции. Радиус инерции -
; Jx=Fix2, Jy=Fiy2.
Если Jx и Jy главные моменты инерции, то ix и iy - главные радиусы инерции. Эллипс, построенный на главных радиусах инерции как на полуосях, называется эллипсом инерции. При помощи эллипса инерции можно графически найти радиус инерции ix1 для любой оси х1. Для этого надо провести касательную к эллипсу, параллельную оси х1, и измерить расстояние от этой оси до касательной. Зная радиус инерции, можно найти момент инерции сечения относительно оси х1: . Для сечений, имеющих более двух осей симметрии (например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех центральных осей равны между собой, Jxy=0, эллипс инерции обращается в круг инерции.
Моменты сопротивления
Осевой момент сопротивления - отношение момента инерции относительно оси к расстоянию от нее до наиболее удаленной точки сечения.
Особенно важны моменты сопротивления относительно главных центральных осей:
прямоугольник:
трубчатое сечение (кольцо) :
Wx=Wy= , где = dН/dB.
Полярный момент сопротивления - отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения:
Для круга Wр= .
Растяжение и сжатие
Нормальное напряжение [Па], 1Па (паскаль) = 1 Н/м2,
106Па = 1 МПа (мегапаскаль) = 1 Н/мм2
N - продольная (нормальная) сила [Н] (ньютон) ; F - площадь сечения [м2]
Относительная деформация [безразмерная величина];
L - продольная деформация [м] (абсолютное удлинение), L - длина стержня [м].
Закон Гука - = Е
Е - модуль упругости при растяжении (модуль упругости 1-го рода или модуль Юнга) [МПа]. Для стали Е= 2105МПа = 2106 кг/см2 (в «старой» системе единиц).
(чем больше Е, тем менее растяжимый материал)
; - закон Гука
EF - жесткость стержня при растяжении (сжатии).
При растяжении стержня он «утоньшается», его ширина - а уменьшается на поперечную деформацию - а.
Относительная поперечная деформация.
Коэффициент Пуассона [безразмерная величина];
лежит в пределах от 0 (пробка) до 0, 5 (каучук) ; для стали 0, 250, 3.
Если продольная сила и поперечное сечение не постоянны, то удлинение стержня:
Работа при растяжении: , потенциальная энергия:
Учет собственного веса стержня
Продольная сила N (z) = P + FL;
Р - сила, действующая на стержень, - удельный вес, F - площадь сечения.
Максимальное напряжение: . Деформация:
Условие прочности при растяжении (сжатии) max ,
Допускаемое напряжение на растяжение (сжатие).
У чугуна [раст][сж], у стали и др. пластичных материалов [раст]=[сж].
Основные механические характеристики материалов
п- предел пропорциональности, т- предел текучести, В- предел прочности или временное сопротивление, к- напряжение в момент разрыва.
Хрупкие материалы, напр., чугун разрушаются при незначительных удлинениях и не имеют площадки текучести, лучше сопротивляются сжатию, чем растяжению.
Допускаемое напряжение, 0- опасное напряжение, n - коэф. запаса прочности. Для пластичных материалов 0 = т и n = 1, 5, хрупких 0 = В, n = 3.
Линейное напряженное состояние
напряжения по наклонной площадке:
нормальное: , касательное:
F - площадь наклонной площадки.
Нормальные напряжения положительны, если они растягивающие; касательные напряжения положительны, если они стремятся повернуть рассматриваемый элемент (нижняя часть) по часовой стрелке (на рис. все положительно). Наибольшие нормальные напряжения возникают по площадкам перпендикулярным к оси стержня (=0, cos=1, max=)
На перпендикулярных площадках: = - (90 -)
; , т. е. = - .
Наибольшие касательные напряжения действуют по площадкам, составляющим угол 45о к оси стержня (=45о, sin2=1, max= /2)
Размещено на Allbest.ru
Подобные документы
Плоское напряженное состояние главных площадок стального кубика. Определение величины нормальных и касательных напряжений по граням; расчет сил, создающих относительные линейные деформации, изменение объема; анализ удельной потенциальной энергии.
контрольная работа , добавлен 28.07.2011
Особенности и суть метода сопротивления материалов. Понятие растяжения и сжатия, сущность метода сечения. Испытания механических свойств материалов. Основы теории напряженного состояния. Теории прочности, определение и построение эпюр крутящих моментов.
курс лекций , добавлен 23.05.2010
Исследование напряжённого состояние в точке. Изучение главного касательного напряжения. Классификация напряжённых состояний. Определение напряжений по площадкам параллельным направлению одного из напряжений. Дифференциальные уравнения равновесия.
курсовая работа , добавлен 23.04.2009
Определение: инвариантов напряженного состояния; главных напряжений; положения главных осей тензора напряжений. Проверка правильности вычисления. Вычисление максимальных касательных напряжений (полного, нормального и касательного) по заданной площадке.
курсовая работа , добавлен 28.11.2009
Методическое указание по вопросам расчётов на прочность при различных нагрузках и видах деформации. Определение напряжения при растяжении (сжатии), определение деформации. Расчеты на прочность при изгибе, кручении. Расчетно-графические работы, задачи.
контрольная работа , добавлен 15.03.2010
Понятие о возможных перемещениях. Действительные работы внешних и внутренних сил. Потенциальная энергия стержневой системы. Теоремы Клапейрона и Бетти. Применение интеграла и формулы Мора, закона Гука. Определение перемещений методами теории упругости.
презентация , добавлен 24.05.2014
Методические указания и задания по дисциплине "Сопротивление материалов" для студентов-заочников по темам: растяжение и сжатие стержня, сдвиг, кручение, теория напряженного состояния и теория прочности, изгиб прямых стержней, сложное сопротивление.
методичка , добавлен 22.01.2012
Потенциальная энергия заряда в однородном поле и потенциальная энергия взаимодействия точечных зарядов. Понятие разности потенциалов. Связь напряжения и напряженности. Принцип суперпозиции для потенциалов. Понятие эквипотенциальных поверхностей.
контрольная работа , добавлен 06.10.2013
Применения МД для исследования пластической деформации кристаллов. Алгоритм интегрирования по времени. Начальное состояние для кристалла с дефектами. Уравнение для ширины ячейки моделирования. Моделирования пластической деформации ГПУ кристаллов.
дипломная работа , добавлен 07.12.2008
Определение напряжений при растяжении–сжатии. Деформации при растяжении-сжатии и закон Гука. Напряженное состояние и закон парности касательных напряжений. Допускаемые напряжения, коэффициент запаса и расчеты на прочность при растяжении-сжатии.
Схемы напряженного состояния графически отображают наличие и направление главных напряжений в рассматриваемой точке тела. Напряжения в точке изображаются как напряжения на трех бесконечно малых гранях куба, соответственно перпендикулярных главным осям. Возможны девять схем напряженного состояния (рисунок, позиция а). Напряженное состояние в точке может быть линейным, плоским или объемным.
Схемы с напряжениями одного знака называют одноименными, а с напряжениями разных знаков – разноименными. Условно растягивающие напряжения считают положительными, с сжимающие – отрицательными.
Схемы напряженного и деформированного состояний
а — напряженное состояние; б — деформированное состояние
I – линейное напряженное состояние; II – плоское напряженное состояние; III – объемное напряженное состояние
Схема напряженного состояния оказывает влияние на пластичность металла. На значение главных напряжений оказывают существенное влияние силы трения, возникающие в месте контакта с инструментом, и форма инструмента. В условиях всестороннего неравномерного сжатия при , ковке, сжимающие напряжения препятствуют нарушению межкристаллических связей, способствуют развитию внутрикристаллических сдвигов, что благоприятно сказывается на процессах обработки металлов давлением (см. все записи с тегом ). В реальных процессах обработки давлением в большинстве случаев встречаются схемы всестороннего сжатия и состояния с одним растягивающим и двумя сжимающими напряжениями.
Схема деформированного состояния графически отображает наличие и направление деформации по трем взаимно перпендикулярным направлениям. Возможны три схемы деформированного состояния (рисунок, позиция б).
При схеме Д I уменьшаются размеры тела по высоте, за счет этого увеличиваются два других размера (
Понятие напряженного состояния Пусть имеется упругое тело, нагруженное уравновешенной системой пространственных сил (рис. 1.1). Чтобы определить напряжение в произвольной точке А, нужно в соответствии с принятым методом сечений провести через точку А плоскость либо 1-1, либо 2-2, либо любую другую. Тогда внутреннее усилие, отнесенное к единице площади сечения, внутри которой располагается точка А, и дает искомое напряжение. Напряжения зависят от выбора положения сечения, от наклона площадки, поэтому для одной и той же точки на каждой плоскости будут возникать разные напряжения как по величине, т ак и по направлению к этой площадке. Для понимания этого явления проведем в окрестности точки А произвольно три взаимно перпендикулярных пары параллельных плоскостей, расстояние между которыми равно единице линейного измерения. Эти плоскости вырежут из тела объем в виде кубика со стороной, равной единице (рис. 1.2). На каждой из шести граней этого элемента будет действовать свое полное напряжение p , которое может быть разложено на нормальную и касательную составляющие (рис. 1.3). В свою очередь, касательное напряжение может быть разложено по направлениям, параллельным ребрам вырезанного элемента (рис. 1.3). Если эту операцию выполнить для других граней вырезанного кубика и учесть закон парности касательных напряжений, можно получить распределение напряжений, показанное на рис. 1.4. Здесь изображены только напряжения на видимых гранях элемента. Такие же напряжения должны быть показаны и на невидимых гранях. Совокупность всех этих векторов напряжений и будет характеризовать напряженное состояние в точке. На рис. 1.4. обозначения векторов напряжений производятся из следующих соображений. Координатные оси совмещены с ребрами кубика. Грани кубика обозначаются по индексам нормалей, которые параллельны соответствующим осям. Например, на верхней грани нормаль к ней параллельна оси Z , поэтому нормальное напряжение на этой площадке (грани) обозначено z , а в обозначении касательных напряжений добавляется еще один индекс, показывающий, параллельно какой оси направлено это напряжение. Так, y означает, что касательное напряжение действует на площадке, перпендикулярной оси Z и параллельно оси Y . Аналогично обозначены все другие векторы напряжений. Из закона парности касательных напряжений получаем, что Из этого следует, что по граням элемента действует всего шесть неизвестных: три нормальных и три касательных напряжений. В курсе «Теория упругости» доказывается, что на гранях вырезанного элемента не будет действовать касательных напряжений аналогично тому, как это рассмотрено для случая простого растяжения. Такой повернутый элемент показан на рис. 1.5. Это положение образованно путем вращения элемента, показанного на рис. 1.4 вокруг осей, параллельных осям ox , oy , oz . На гранях этого повернутого элемента будут действовать только нормальные напряжения, которые принято обозначать. Такие площадки (грани), на которых отсутствуют касательные напряжения, называют главными площадками, а нормальные напряжения, действующие на этих площадках, называют главными нормальными напряжениями. Наибольшее, в алгебраическом понятии, из главных напряжений обозначают, наименьшее, а промежуточное по величине 2 , т. е. соблюдается условие. Например, если заданы напряжения: 80 МПа, 60 МПа и 40 МПа, то соответственно получим: σ 1.2. Виды напряженного состояния Различают 3 вида: объемное, плоское и линейное напряженное состояние. Объемное напряженное состояние – это такое, когда по главным площадкам действуют все три главных напряжения (рис. 4.6). В случае плоского напряженного состояния одно из главных напряжений равно нулю. При этом принято изображать рассматриваемый элемент не в виде куба, а в виде квадрата, совмещая грани кубика, на которых нет напряжений, с плоскостью чертежа (рис. 1.7). Линейное напряженное состояние характеризуется тем, что любые два главных напряжения равны нулю (рис. 1.8): Линейное напряженное состояние испытывают стержни при простом растяжении или сжатии. Из более сложных напряженных состояний ограничимся рассмотрением плоского напряженного состояния, тем более, что подавляющее большинство практических задач техники сводится к этому виду напряженного состояния. 1.3. Напряжения на произвольной площадке Напишем (без вывода) зависимость между главными нормальными напряжениями и напряжениями на произвольной площадке для общего случая объемного напряженного состояния. Пусть имеется элемент, по граням которого действуют главные напряжения 1, (рис. 1.9). Применим метод сечений и рассечем кубик произвольной плоскостью. На рисунке полученное сечение заштриховано. Найдем напряжения на этой площадке. Для этого отбросим переднюю часть, а оставшуюся вычертим, и на площадке, ставшей гранью тетраэдра, покажем напряжения, заменяющие действия отброшенной части кубика на оставшуюся (рис. 1.10). Положение площадки) по отношению к граням кубика определяется величиной углов между осями 0-1, 0-2, 0-3 и направлением внешней нормали n к площадке. Нормаль построим, проведя прямую из начала координат перпендикулярно к площадке. Направления осей 0-1, 0-2, 0-3 соответствуют направлениям главных напряжений В этом случае величина нормального и касательного напряжений на площадке выразится следующими формулами, которые выводятся в курсе «Теория упругости»: Из формул (4.2) и (4.3) можно получить формулы для более простых напряженных состояний. Для случая линейного напряженного состояния полагаем 230 получим Формулы (1.4) и (1.5) отражают случай простого растяжения (сжатия). Для плоского напряженного состояния, приняв, получим напряжения на взаимно перпендикулярных площадках. Из рис. 1.11 видно, что ак как все угловые величины выражены через 1, то можно считать 1. Подставляя эти значения в формулу (1.2), получим: Для определения напряжений на площадке нужно в формулах (1.6) и (1.7) заменить значение угла на угол (900 ); после подстановки будем иметь: т.е. опять наблюдаем проявление закона парности касательных напряжений Сложим почленно выражения (1.6) и (1.8), получим Алгебраическая сумма нормальных напряжений по двум взаимно перпендикулярным площадкам постоянна и равна сумме двух главных напряжений. Определим, при каких значениях угла нормальное напряжение будет иметь экстремальное значение. Для этого вычислим первую производную от функции (формула 1.2) по углу и приравняем ее к нулю: Следовательно, экстремальные значения нормальных напряжений возникают на тех площадках, на которых касательные напряжения равны нулю. Такие площадки называются главными, значит, главные нормальные напряжения и будут экстремальными, т. е. если одно из них достигает наибольшего значения1 , то другое будет иметь наименьшее значение 2 . Можно показать, что положение главных площадок или угол 0, на который нужно повернуть элемент, чтобы его грани стали главными площадками, определяется следующей формулой: Отсчет угла по этой формуле всегда производится от направления против хода часовой стрелки, если значение угла получается положительным, или по ходу часовой стрелки при отрицательном значении угла. Вопрос о том, которая из двух площадок будет иметь обозначения или , определяется неравенством . Величина главных нормальных напряжений определяется по формуле Для получения значения перед вторым членом используется знак (+) плюс, для получения ─ знак (-) минус. 1.4. Понятия о траекториях главных напряжений Наглядное представление о потоке внутренних сил в нагруженном теле дают траектории главных напряжений. Так называется линия, в каждой точке которой касательная совпадает с направлением главного напряжения в этой точке. При простом растяжении бруса (рис. 1.12) траекториями главных напряжений, очевидно, являются прямые, параллельные и перпендикулярные его оси. Если во всех точках трубы, рассмотренной в конце предыдущего параграфа, наметим направление главных напряжений, то получим сетку взаимно ортогональных кривых – траекторий главных сжимающих и растягивающих напряжений (рис 1.13). Прямоугольный элемент, выделяемый траекториями, испытывает растяжение (сжатие) в перпендикулярных направлениях, а касательные напряжения на его гранях отсутствуют. В указанных примерах величина главного напряжения во всех точках тела одинакова. В общем случае главное напряжение меняет величину при движении вдоль траектории. Знание траектории главных напряжений во многих случаях даёт возможность придать рациональную форму проектируемой детали или части конструкции.
Уже на примерах растяжения и сдвига мы имели возможность убедиться в том, что напряжения в площадке, проходящей через заданную точку напряженного тела, зависят от ее ориентации. С поворотом площадки меняются в определенной зависимости и напряжения. Совокупность напряжений, возникающих во множестве площадок, проходящих через рассматриваемую точку, называется напряженньш состоянием в точке. Напряженное состояние поддается анализу не только в частных случаях растяжения и сдвига, но и в общем случае нагружения тела. В настоящей главе этот вопрос и будет рассмотрен. Заметим, что исследование законов изменения напряжений в точке не является чисто отвлеченным. Оно необходимо для последующего решения более сложных задач и в первую очередь для расчетов на прочность в общих случаях нагружения.
Положим, имеется некоторое тело (не обязательно упругое), нагруженное произвольной системой сил (рис. 7.1). При
переходе от точки к точке напряженное состояние меняется достаточно медленно и всегда имеется возможность выбрать в окрестности произвольно взятой точки А (см. рис. 7.1) такую достаточно малую область, для которой напряженное состояние можно было бы рассматривать как однородное. Понятно, что такой подход возможен только в пределах принятой ранее гипотезы сплошной среды, допускающей переход к предельно малым объемам.
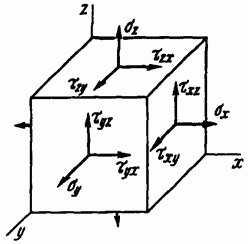
Чтобы охарактеризовать напряженное состояние в точке А, представим себе, что через нее проведены три секущие площадки и установлены возникающие в них напряжения. Затем в окрестности исследуемой точки шестью сечениями выделим элементарный объем в виде прямоугольного параллелепипеда (рис. 7.2). Если размеры параллелепипеда уменьшать, он будет стягиваться в эту точку. В пределе все грани параллелепипеда пройдут через точку А, и напряжения в соответствующих секущих плоскостях можно рассматривать как напряжения в исследуемой точке.
Полное напряжение, возникающее на секущей площадке, может быть разложено на три составляющие: одну по нормали к площадке и две в плоскости сечения. Нормальное напряжение будем обозначать по-прежнему буквой а с индексом, соответствующим осям х, у и z (см. рис. 7.2). Касательное напряжение обозначим буквой с двумя индексами: первый соответствует оси, перпендикулярной к площадке, а второй -
оси, вдоль которой направлен вектор . Ориентация самих осей является произвольной.
Нормальные растягивающие напряжения а будем считать положительными, сжимающие - отрицательными. Что касается знака напряжений то здесь обусловливать его не будем, поскольку в пределах рассматриваемых ниже задач знак роли не играет.
Напряжения, возникающие на трех гранях элемента (на трех взаимно перпендикулярных плоскостях, проходящих через точку) показаны на рис. 7.2. На невидимых гранях элемента возникают соответственно такие же напряжения, но противоположно направленные.
Система сил, приложенных к элементу, должна удовлетворять условиям равновесия. Поскольку на противоположных гранях возникают противоположные по направлению силы, то первые три условия равновесия удовлетворяются тождественно, и суммы проекций всех сил на оси х, у и z равны нулю независимо от значений возникающих напряжений. Остается проверить, обращаются ли в нуль суммы моментов всех сил относительно осей При составлении уравнений равновесия легко обнаружить, что момент каждой силы уравновешивается моментом противоположной силы, расположенной на невидимой грани. Исключение составляют касательные силы. Например, для оси х условие равенства нулю суммы моментов соблюдается в том случае, если момент силы равен моменту силы , т. е.
Аналогично могут быть написаны еще два уравнения равновесия. Тогда получаем
Таким образом, на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к общему ребру, равны и направлены обе либо к ребру, либо от ребра. Это и есть закон парности касательных напряжений, сформулированный в общем виде (см. также § 1.5). Он справедлив для всех точек нагруженного тела независимо от
вида приложенных нагрузок и свойств материала. Следствием из условия парности касательных напряжений является то, что на гранях выделенного элемента (см. рис. 7.2) имеем не девять, а только шесть независимых компонент напряжений, поскольку касательные напряжения попарно равны.
Анализ напряженного состояния в точке начинают всегда с определения напряжений на гранях выделенного в окрестности точки элемента. Через точку проводят три взаимно перпендикулярные плоскости, ориентацию которых выбирают произвольно, но так, чтобы напряжения в площадках могли бы быть определены наиболее простым путем.
Пример 7.1. Выявить напряженное состояние в точках А к В растянутого и одновременно закрученного стержня (рис. 7.3, а).
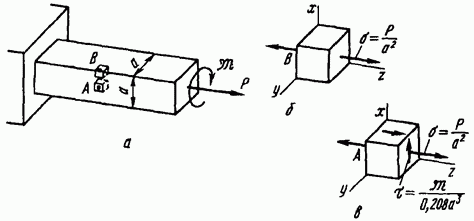
В окрестности заданных точек секущими плоскостями выделяем элементарный объем. Ориентацию плоскостей выбираем таким образом, чтобы напряжения можно было определить наиболее простым способом. В данном случае естественной является ориентация плоскостей вдоль и поперек оси стержня. На рис. 7.3, а секущие плоскости в окрестности точек А и В показаны штриховыми линиями. Вынесем выделенные элементы за пределы нагруженного тела и представим их в увеличенном масштабе с сохранением ориентации плоскостей (рис. 7.3, б и в).
В результате действия силы Р в поперечных сечениях стержня возникает нормальное напряжение Векторы соответствующих напряжений вычерчиваем на гранях элементов. В результате действия момента в поперечных и продольных сечениях возникают касательные напряжения. В точке А напряжение гтлх в точке В напряжение Векторы также вычерчиваем на гранях элемента. В итоге имеем: в точке в точке


