Расчета методом сил многопролетных неразрезных балок
О принципе расчета статически неопределимых систем уже было сказано ранее (см. п.1.2). Рассмотрим на примере, как это делается применительно к балкам.
Пример 8
Определить размеры h , b прямоугольного поперечного сечения стальной балки (рис. 32, а ), если [σ и ] = 160 МПа, E = 2·10 5 МПа и h/b = 2. Определить прогибы посредине пролета балки и на конце консоли.
Число неизвестных реакций 4, уравнений статики 3: балка один раз статически неопределима. Целесообразные уравнения статики:
Дополнительное уравнение составим, исходя из условия, что на опоре B прогиб равен нулю:
Так как начало координат помещено в защемлении, начальные параметры y 0 = 0 и φ 0 = 0. Тогда из уравнения прогибов получим:
![]() (14)
(14)
Из уравнений (13) и (14) следует: ![]() , m c =
7 кН∙м.
, m c =
7 кН∙м.
Определим опорную реакцию B :
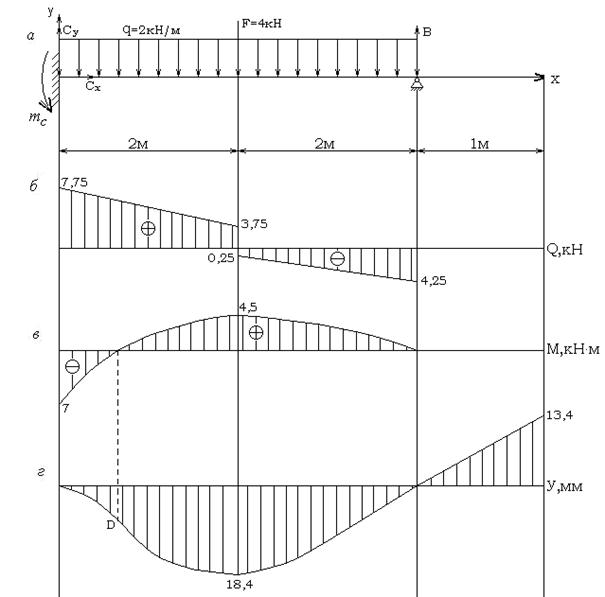
Рис. 32. Эпюры поперечных сил Q ,
изгибающих моментов M и прогибов y
Проверка вычислений реакций:
Эпюры и показаны на рис. 32, б, в .
Размеры сечения балки определим из условия прочности по нор-мальным напряжениям:
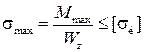 ;
; 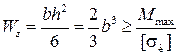 ;
;
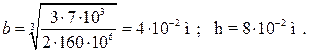
Момент инерции сечения
![]()
Жесткость сечения
Прогиб посередине пролета балки
Прогиб на конце консоли
откуда 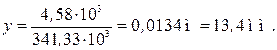
Изогнутая ось балки показана на рис. 32, г . Необходимо отметить,
что консольная часть балки не деформируется , но перемещается за счет деформации пролетной части. Точка D – точка перегиба упругой линии.
Задача 9. Расчет статически неопределимой балки
Произвести расчет статически неопределимой балки (рис. 33).
Материал балки – сталь ![]() Данные к задаче приведены
Данные к задаче приведены
План решения задачи:
1) раскрыть статическую неопределимость;
2) построить эпюры Q и M ;
3) определить номер профиля сечения;
4) изобразить изогнутую ось балки, определив величины погибов в
характерных сечениях (не менее двух).
Примечание. Для раскрытия статической неопределимости следует
составить уравнения прогибов для шарнирной опоры и уравнение моментов относительно той же опоры.
Таблица 10
Данные к задаче 9
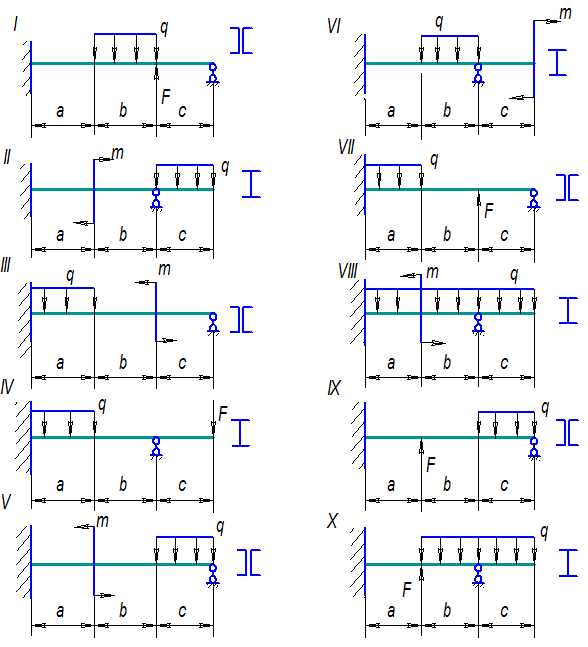
Рис. 33. Cхемы балок к задаче 9
Вопросы для самоконтроля
1. Какие системы называются статически неопределимыми и чем они отличаются от статически определимых систем?
2. Что такое основная система метода сил?
3. В чем заключается выбор основной системы?
4. Каков физический смысл уравнений деформаций?
1. Любое тело, если свобода его передвижения не ограничена, может перемещаться в пространстве, как ему заблагорассудится. Закономерности движения таких тел изучает кинематика, а возникновение и влияние сил, к такому движению приводящих - удел динамики. В трехмерном мире, в котором мы живем, существует свобода перемещений в трех направлениях вверх-вниз, вперед-назад и вправо-влево, или три степени свободы. Соответственно, чтобы ограничить свободу передвижения в этих трех направлениях или, выражаясь геометрическим языком - в этих трех плоскостях, исследуемое тело нужно связать с каким-нибудь другим неподвижным телом и количество таких связей, именуемых кинематическими, должно быть не менее трех. Но и это еще не все, если кинематические связи не защищают от возможности вращения, то у тела остается еще 3 степени свободы - вращаться в трех плоскостях и потому на физическое тело нужно наложить 6 связей, чтобы полностью ограничить его свободу. И если задача мудрого правителя - ограничивать свободу передвижения человеческих тел, являющихся одновременно и физическими телами, таким образом, чтобы при этом оставалась полная иллюзия свободы, то задача мудрого строителя - проектировать строительные конструкции так, чтобы создавалась полная иллюзия отсутствия свободы перемещений. Такое состояние строительной конструкции называется статическим равновесием, а кинематические связи рассматриваются как опоры.
2. Одним из видов строительных конструкций являются балки. Балки с точки зрения строительной механики рассматриваются как стержни, т.е. такие физические тела, высота и ширина которых значительно меньше длины. Для решения множества задач рассматривать балку как объемное физическое тело вовсе не обязательно, вполне достаточно ограничиться рассмотрением "плоской" задачи, т.е. рассматривать балку, как некий условно плоский и даже одномерный стержень (влияние геометрических размеров поперечных сечений балки учитывается на следующем этапе расчета). Таким образом для ограничения свободы плоского стержня необходимо наложить 4 кинематических связи. А если учесть, что балка сама по себе есть связь между своими точками, то количество связей можно уменьшить до 3. При этом две связи (показаны на рисунке 219.2 фиолетовым цветом) ограничивают перемещение относительно оси у , а одна связь (показана на рисунке 219.2 синим цветом) и сама балка, имеющая некоторую жесткость, ограничивают перемещения по оси х:
Рисунок 219.2 . Шарнирно опертая безконсольная балка.
При этом нельзя забывать, что реальная балка перекрытия или плита, опертая на стены дома, и шарнирно опертая безконсольная балка, показанная на рисунке 219.2 - это принципиально разные вещи. А для значительного упрощения расчетов допускается предполагать, что реальная балка соответствует данной расчетной схеме.
3. Для расчета любой строительной конструкции необходимо знать значение всех сил, действующих на конструкцию.
4. Предполагается, что любое тело, в нашем случае балка, имеющая опоры, будет оставаться в состоянии статического равновесия после замены кинематических связей - опор - соответствующими реактивными силами, или как их чаще называют - опорными реакциями. На основании этого можно составить 2 уравнения равновесия системы, относительно оси х и относительно оси у .
∑ у = 0 у . (253.1.1)
∑ х = 0 - для сил, действующих вдоль оси х . (253.1.2)
Однако этих двух уравнений для определения трех неизвестных явно недостаточно, нужно составить еще хотя бы одно уравнение.
5. Сделать это помогает переход на следующий уровень, когда рассматриваются не сами силы, а моменты, этими силами создаваемые. Как то установил Архимед, чем больше расстояние от точки приложения силы до рассматриваемой точки, тем больше значение момента. Соответственно, если есть некая надежная точка опоры, то если на эту точку опереть некий стержень таким образом, чтобы длина стержня с одной стороны (длинное плечо) была много больше длины с другой стороны (короткое плечо), а затем приложить к концам стержня некоторые силы, то стержень будет оставаться в состоянии равновесия, если сила, приложенная к длинному плечу, будет меньше силы, приложенной к короткому плечу, во столько раз, во сколько длинное плечо длиннее короткого плеча. А если значение силы, приложенной к длинному плечу будет хотя бы немного больше, то стержень начнет вращаться относительно точки опоры. Отсюда и проистекает знаменитое высказывание Архимеда: "дайте мне точку опоры и я переверну мир". И хотя надежную точку опоры Архимеду так никто и не дал, да и стержень, который Архимед намеревался использовать в качестве рычага, следовало бы просчитать на прочность, тем не менее открытие Архимеда мир действительно перевернуло и теперь этим открытием пользуются не только инженеры, рассчитывающие строительные конструкции, но и все другие люди, пользующиеся фомкой.
Если рассматривать открытие Архимеда с позиции строительной механики, то точка приложения сосредоточенной нагрузки, центр тяжести распределенной нагрузки или приведенный центр тяжести всех приложенных к балке нагрузок - это и есть та точка опоры, относительно которой момент, создаваемый реактивной силой правой опоры, равен моменту, создаваемому реактивной силой левой опоры, а сама балка находится в состоянии статического равновесия. Если перевести открытие Архимеда на математический язык, то момент - есть некая функция у = f(x), М = Qx или М = ∫Qdx. На основании этого можно составить как минимум одно дополнительное уравнение, позволяющее определить значение одной из опорных реакций. Например, для шарнирно закрепленной балки значение изгибающего момента в точке приложения первой силы и в точке приложения последней силы будет равно нулю.
Если бесконсольная балка длиной l имеет шарнирно неподвижную опору А и шарнирно подвижную опору В (см. рис.219.2), и к этой балке приложена только сосредоточенная нагрузка Q на расстоянии х от опоры В , то уравнение моментов в точке В , исходя из условия статического равновесия, будет иметь следующий вид:
М B = Аl - Qx = 0 (253.1.3)
Таким образом любая "плоская" строительная конструкция, имеющая 3 кинематические связи (не пересекающиеся в одной точке, что обеспечивает геометрическую неизменяемость системы) и некоторую жесткость, находится в состоянии статического равновесия, а для определения опорных реакций такой конструкции достаточно 2 уравнений равновесия системы и одного уравнения моментов.
6. Между тем у балки, как и у любой другой строительной конструкции, может быть не 3 кинематических связи, а 4, 5, 10 и вообще сколь угодно много. Причем балке от этого только лучше, так как чем меньше расстояние между опорами, тем больше несущая способность при тех же геометрических параметрах сечения и прочностных характеристиках. А вот для человека, занимающегося расчетом конструкций, в этом ничего хорошего нет, так как каждая связь сверх трех, обеспечивающих статическое равновесие, является как бы лишней. Количество "лишних" кинематических связей называется степенью статической неопределимости. Определить дополнительные реактивные силы - опорные реакции для таких связей, пользуясь уравнениями равновесия и уравнением моментов, невозможно, нужно составить столько дополнительных уравнений, сколько имеется лишних опор.
7. Сделать это опять помогает переход на следующий уровень, когда дополнительно рассматриваются углы поворота поперечных сечений или прогибы - вертикальные перемещения центров тяжести поперечных сечений балки. Как и изгибающие моменты, углы поворота θ и прогибы f зависят от величины прикладываемой нагрузки и в общем виде эту зависимость можно выразить так:
θ = ∫Мdx/EI = ∫∫Qd 2 x/EI (314.1.1)
f = ∫θdx = ∫∫Md 2 x/EI = ∫∫∫Qd 3 x/EI (314.1.2)
Так как вертикальная шарнирная опора не препятствует повороту, но препятствует вертикальному перемещению (для того она и используется), то сколько бы ни было у балки опор и как бы хитроумно ни была приложена к балке нагрузка, вертикальные перемещения - прогибы - на вертикальных опорах всегда будут равны нулю.
Примечание : Здесь опять же не следует забывать, что в действительности дополнительные вертикальные опоры далеко не всегда обеспечивают отсутствие прогибов на этих опорах. Например, монолитное железобетонное перекрытие по балкам может рассматриваться как многопролетная балка на шарнирных опорах весьма условно, так как балки - промежуточные опоры - под действием нагрузки, передаваемой плитой, также будут прогибаться и потому такую плиту более правильно рассматривать, как балку с крайними шарнирными опорами и промежуточными упруго деформируемыми опорами. Однако это будет после, а нам бы пока разобраться, как рассчитать статически неопределимую балку на шарнирных опорах.
8. Так как прогибы на всех вертикальных шарнирных опорах равны нулю, то любую статически неопределимую балку можно рассматривать как статически определимую, на которую действуют дополнительные силы - неизвестные опорные реакции. Причем действуют таким образом, что прогиб в точках приложения таких сил равен нулю. Это предположение позволяет составить столько дополнительных уравнений, сколько имеется "лишних" связей.
Такой метод расчета называется методом сил (или методом нулевых линейных перемещений)
Рассмотрим, как это делается, на следующем примере:
Имеется двухпролетная неразрезная балка с постоянной жесткостью EI по длине балки, к которой приложена равномерно распределенная нагрузка:
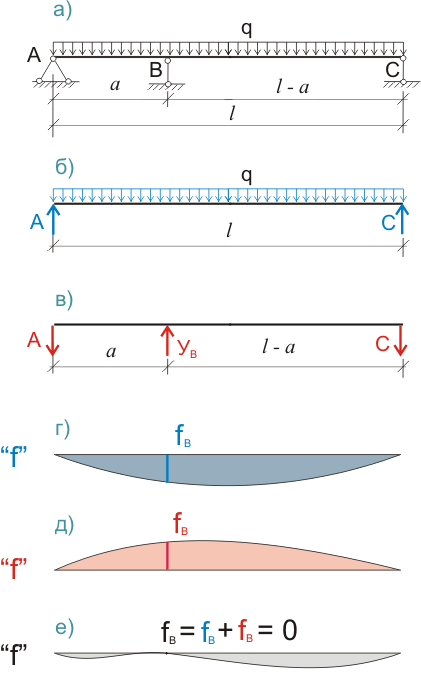
Рисунок 314.1 . Приведение 1 раз статически неопределимой балки к основной и вспомогательной системам.
Такую балку можно рассматривать как обычную однопролетную, а значит, статически определимую балку, показанную на рисунке 314.1.б). Такая балка рассматривается как элемент основной системы. Определить для такой балки опорные реакции, построить эпюры поперечных сил, изгибающих моментов, углов поворота и прогиба - не проблема. В данной статье принципы построения эпюр не рассматриваются, а эпюры поперечных сил, моментов и углов поворота не приводятся, так как нас в данном случае интересует только эпюра прогибов, показанная на рисунке 314.1.г).
Балка, показанная на рисунке 314.1.в) - это элемент вспомогательной системы, которая также является статически определимой и также легко может рассчитываться как и основная система. А неизвестная опорная реакция У В определяется, исходя из принятого нами условия - прогиб балки на опоре В f B = 0 .
В частном случае, когда промежуточная опора В находится посредине основного пролета, т.е. а = l/2 , определение неизвестной опорной реакции много времени не займет, так как при действии равномерно распределенной нагрузки
f l/2 = - 5ql 4 /(384EI) (174.6.4.6)
Соответственно реакции опор для балки основной системы
А = С = ql/2 (314.2.1)
а при действии сосредоточенной нагрузки посредине пролета
f l/2 = У В l 3 /(48EI) (174.6.3.5)
Для такой балки реакции опор составят
А = С = - У В /2 (314.2.2)
и тогда из уравнений (174.6.4.6) и (174.6.3.5) следует, что
5ql 4 /384EI = У В l 3 /48EI (314.2.3)
У В = B = 5ql/8 = 10qa/8 (314.2.4)
Таким образом мы определили неизвестную опорную реакцию В . Соответственно остальные расчетные реакции опор для балки
А = С = А + А = ql/2 - 5ql/16 = 3ql/16 = 3qa/8 (314.2.5)
А момент на средней опоре
M = 3ql 2 /32 - ql 2 /8 = - ql 2 /32 = 3qa 2 /8 -qa 2 /2 = - qa 2 /8 (314.3.1)
Во всех остальных случаях, т.е. когда промежуточная опора находится не посредине пролета, отделаться столь малой кровью уже не получится. Сначала следует определить значение прогиба для основной системы и хотя нагрузка для основной системы не изменится, но изменится положение поперечного сечения, для которого следует определить прогиб.
f а = - θ A а + Aа 3 /6EI - qа 4 /24ЕI = q(2lа 3 - а 4 - l 3 а)/24EI (314.3.1)
Для вспомогательной системы - балки к которой сосредоточенная нагрузка - неизвестная опорная реакция будет приложена не посредине пролета, уравнение прогиба для точки приложения нагрузки будет иметь вид
f a = У В а 2 (l -a) 2 /3lEI (314.3.2)
а опорные реакции составят
А = - У В (l - a)/l; C = - У В а/l (314.3.3)
У В = В = ql(2lа 3 - а 4 - l 3 а)/(8а 2 (l -a) 2) (314.3.4)
Как видим, при смещении дополнительной опоры относительно центра балки определение опорных реакций значительно усложняется.
А если у балки будет не одна "лишняя" опора, а две, то нам придется задействовать вторую вспомогательную систему - балку с нагрузкой, приложенной на второй "лишней" опоре:
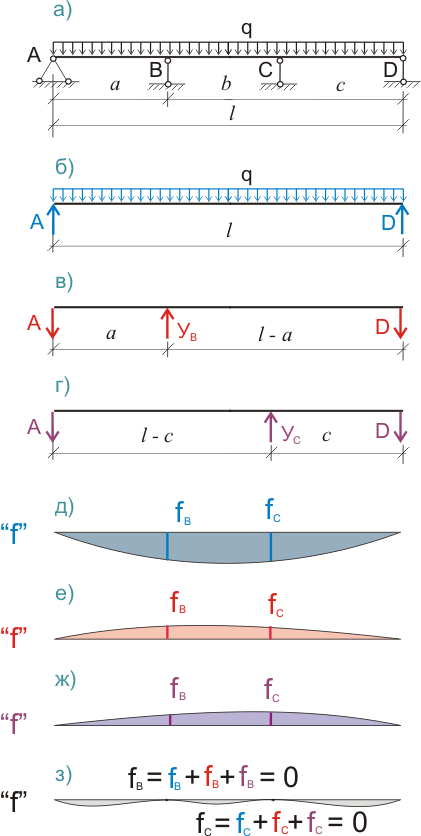
Рисунок 314.2 . Приведение дважды статически неопределимой балки к основной и вспомогательной системам.
А еще это означает, что мы не сможем сразу определить значение одной из неизвестных опорных реакций. Для того, чтобы это сделать, необходимо решить систему из двух уравнений, показанных на рисунке 314.2.з).
А так как статически неопределимых реакций опор может быть сколь угодно много, так что цветов на все не напасешься, да и не всегда есть возможность показать эту разницу цветом, то подобные уравнения записываются в несколько иной форме:
f в0 + f вУв + f вУс = 0 (314.4.1)
f с0 + f сУв + f сУс = 0
А если обозначить статически неопределимые опоры цифрами, а прогиб греческой буквой Δ, то система уравнений будет выглядеть так:
Δ 10 + Δ 1У1 + Δ 1У2 = 0 (314.4.2)
Δ 20 + Δ 2У1 + Δ 2У2 = 0
Это и есть канонические уравнения описанного выше метода сил (метода нулевых линейных перемещений)
Если у балки будет 3 статически неопределимых опоры, то нужно составлять систему из трех уравнений, в каждом из которых будет по 3 неизвестных величины. Для балки с 5 статически неопределимыми опорами потребуется решение системы из 5 уравнений, в каждом из которых будет по 5 неизвестных величин и так далее. Да и нагрузка на многопролетную балку далеко не всегда бывает равномерно распределенной, а значит и с определением расчетных характеристик для балки - основной системы также придется повозиться.
В связи с этим для расчетов балок с большой степенью статической неопределимости используется другой метод, который можно назвать
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Сибирский государственный индустриальный университет»
Кафедра технической механики и графики
Расчет статически неопределимой балки
Методические указания к выполнению расчетно-графической работы
по курсу «Сопротивление материалов»
Новокузнецк
Рецензент:
кандидат технических наук, доцент,
заведующий кафедрой инженерных конструкций
и строительной механики
Н.Н. Алешин
Р24 Расчет статически неопределимой балки: метод. указ. / Сиб.
гос. индустр. ун-т; сост. Ю.А. Епифанцев. – Новокузнецк:
Изд. центр СибГИУ, 2014. – 26с.
Представлены задания к выполнению расчетно-графической работы, включающей раскрытие статической неопределимости балки методом начальных параметров и методом сил с построением ее упругой линии. Приведен пример решения.
Предназначены для студентов, обучающихся по направлениям подготовки 270100.62 Архитектура и 270800.62 Строительство.
Статически неопределимые балки – это балки, имеющие избыточные или «лишние» связи. Отличие статически неопределимых балок от статически определимых заключается в методике определения реактивных сил и моментов. Их расчет нельзя выполнить при помощи одних лишь уравнений равновесия. Необходимо составить дополнительные уравнения (уравнения перемещений), учитывающие характер деформации балки и включающие те же неизвестные.
Для раскрытия статической неопределимости дополнительные уравнения могут быть составлены с использованием различных условий и методов . В данной расчетно-графической работе необходимо провести расчет одной и той же балки с использованием универсального уравнения изогнутой оси балки (метод начальных параметров) и метода сил.
Задание . Для одной из балок, изображенных на рисунке 1, требуется:
1. Построить эпюры поперечных сил Q и изгибающих моментов М;
2. Выполнить кинематическую проверку;
3. Подобрать двутавровое сечение при
4. Определить прогибы в середине межопорного пролета и на конце консоли (при отсутствии консоли величину второго прогиба определить в сечении, отстоящем от правой шарнирной опоры на величину .
5. Построить упругую линию балки.
Данные взять из таблицы 1.
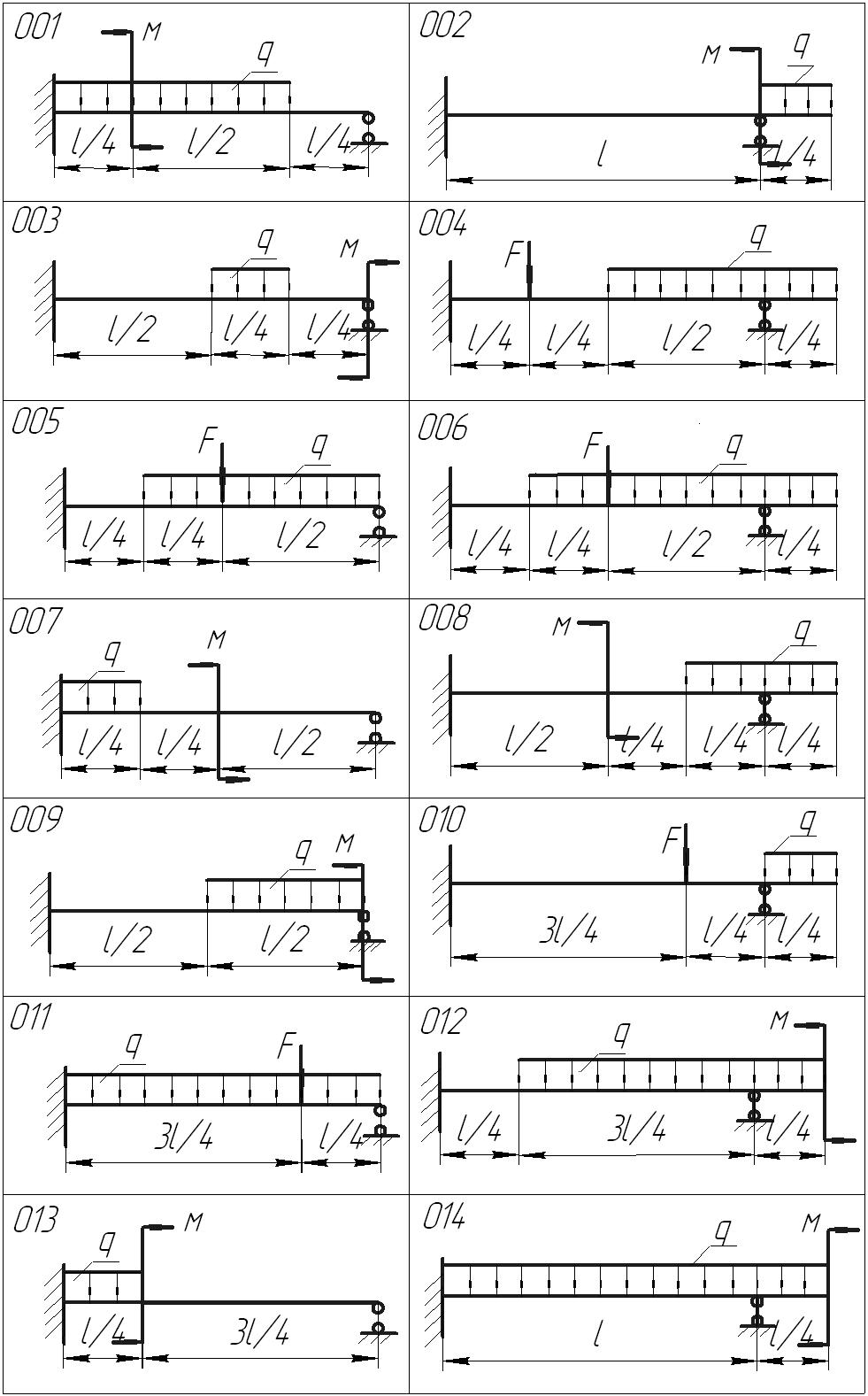
Рисунок 1 – Расчетные схемы
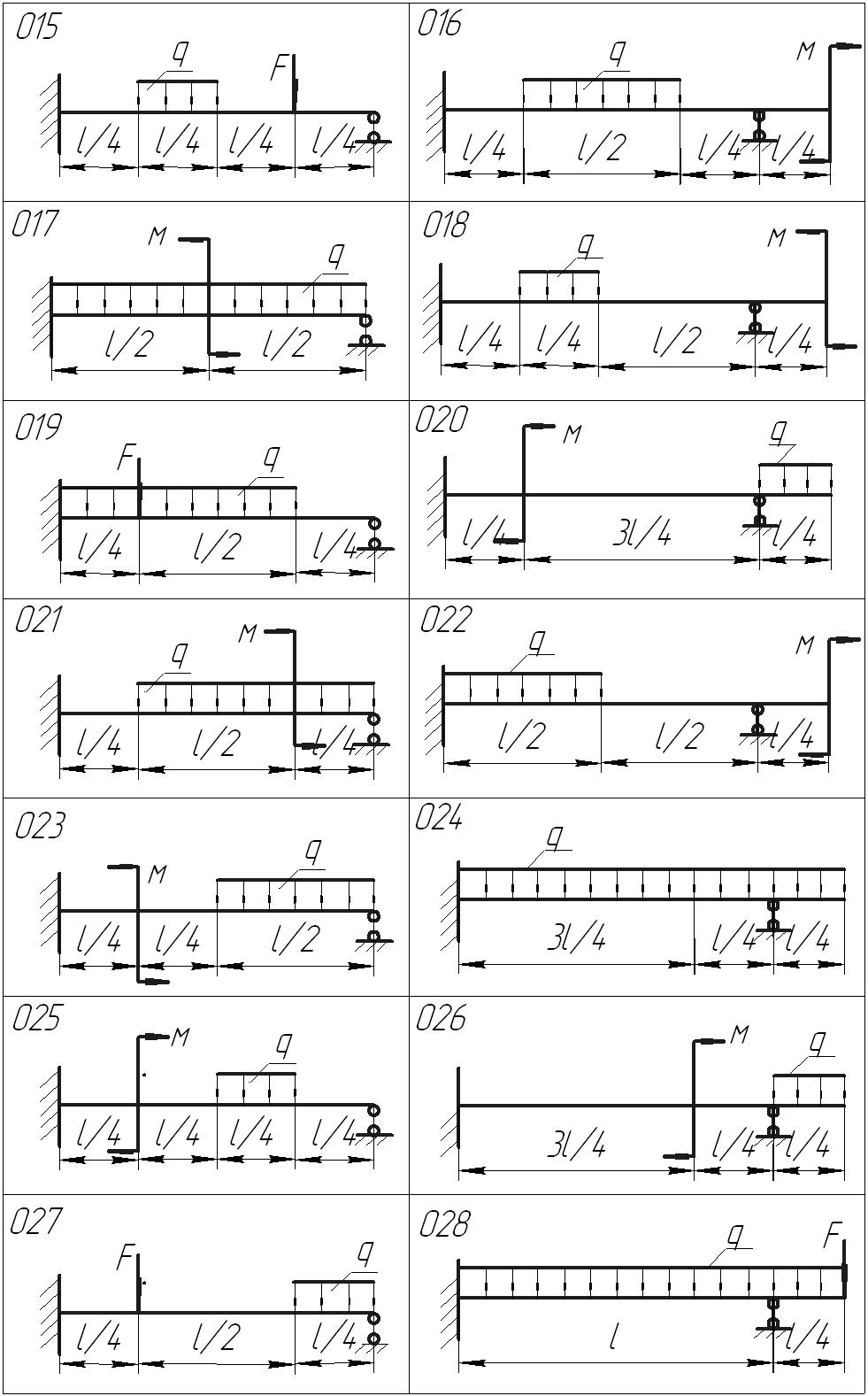
Рисунок 1 – Расчетные схемы
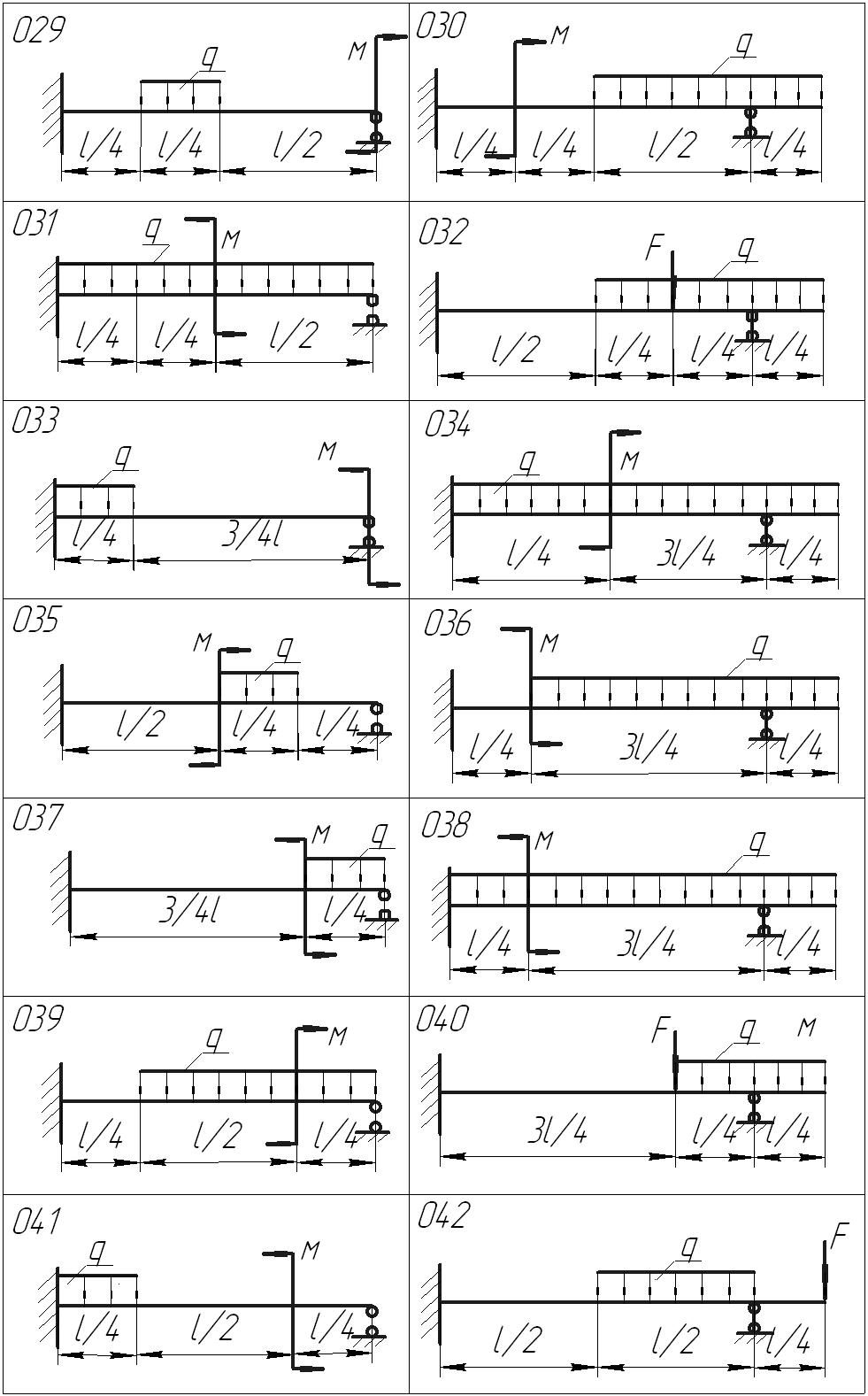
Рисунок 1 – Расчетные схемы
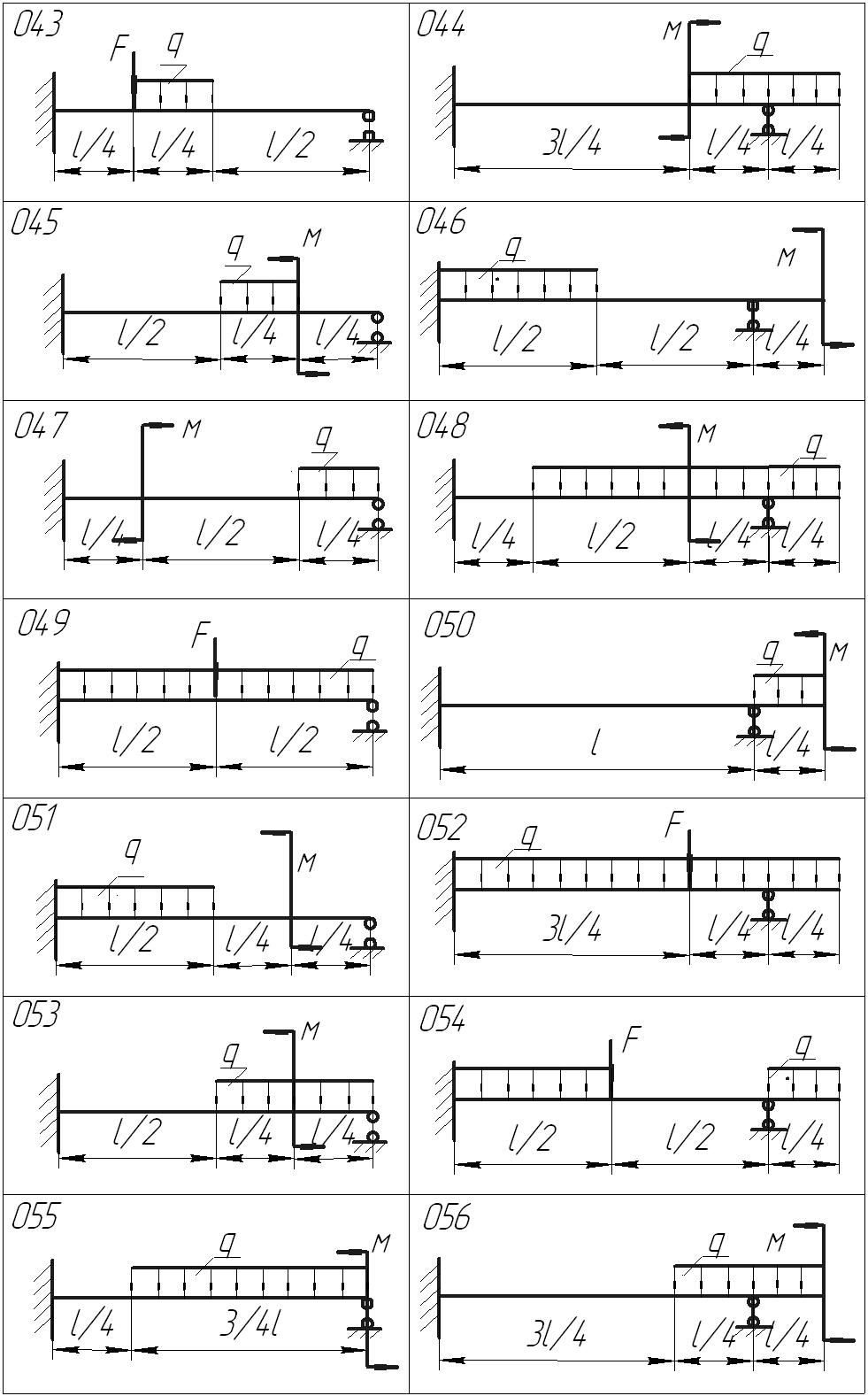
Рисунок 1 – Расчетные схемы

Рисунок 1 – Расчетные схемы
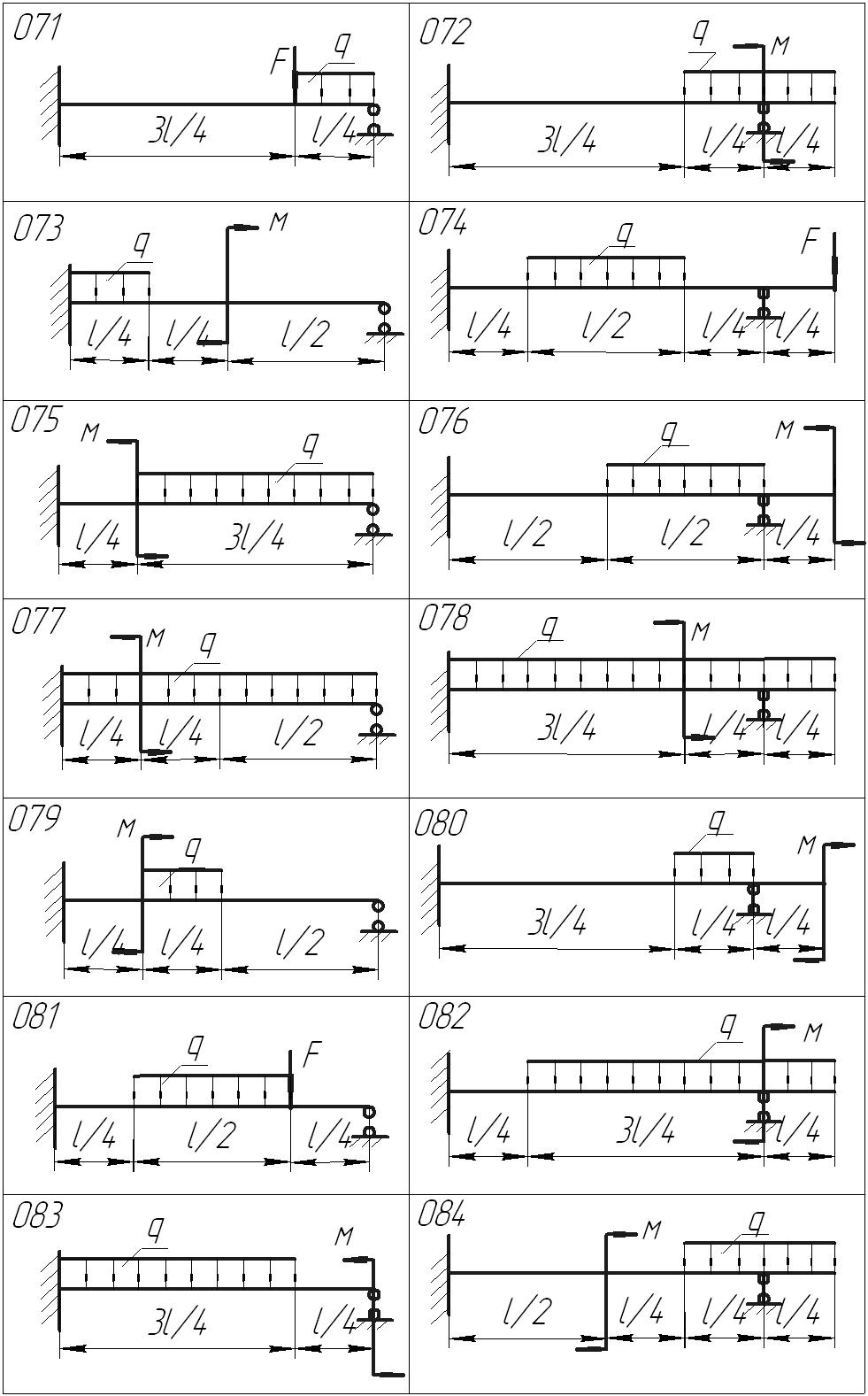
Рисунок 1 – Расчетные схемы
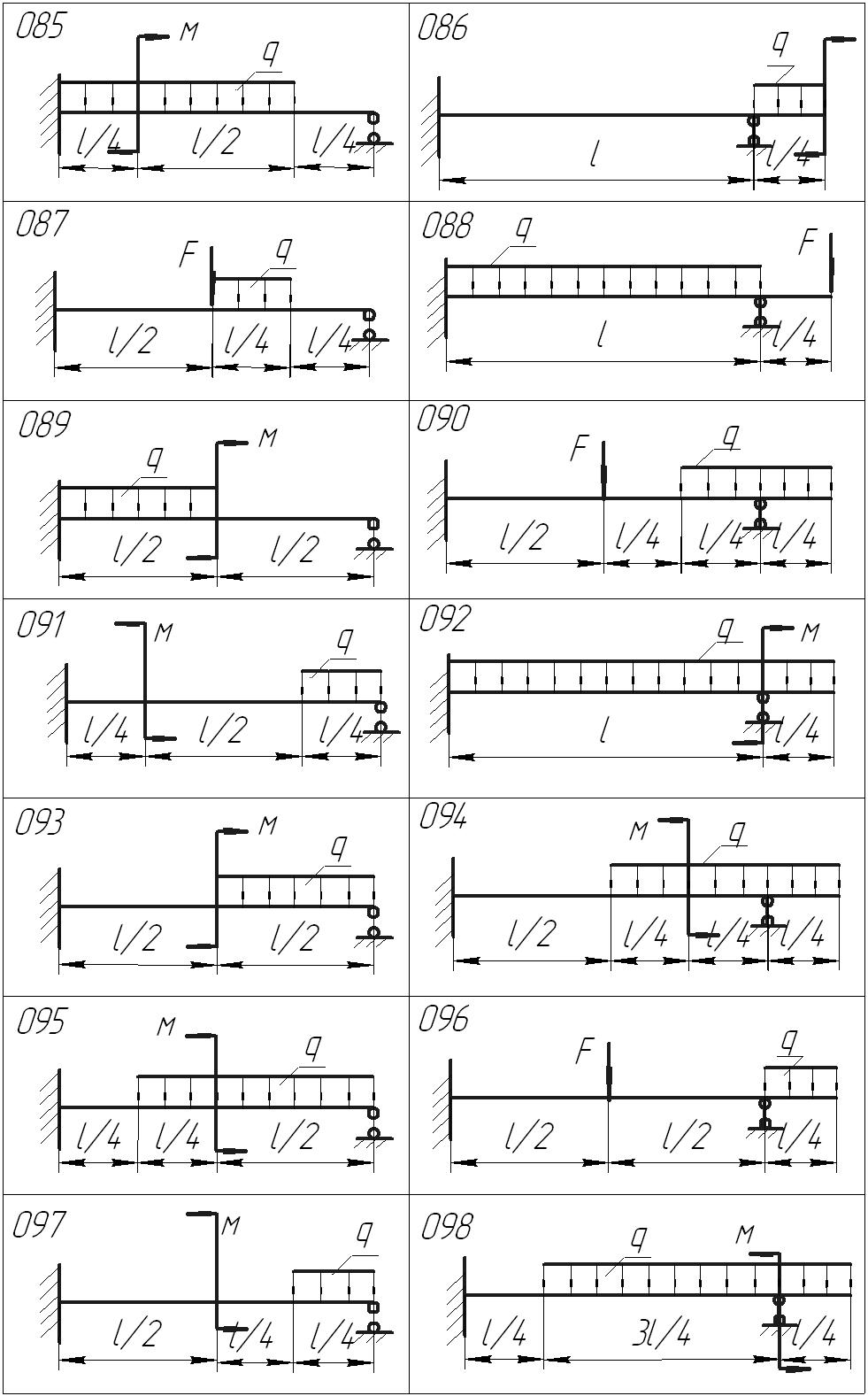
Рисунок 1 – Расчетные схемы
Таблица 1Исходные данные
|
l , м . |
q, кН/м |
М , кНм |
||
Пример . Проведем решение задания для балки, изображенной на рисунке 2а.
Решение
1. Находим степень статической неопределимости (число опорных связей минус число уравнений равновесия)
Значит, данная балка один раз статически неопределима.
2. Воспользуемся уравнениями равновесия в виде сумм моментов внешних нагрузок относительно точек А и В (рисунок 2б):
Для раскрытия статической неопределимости дополнительно к этим уравнениям используем уравнение начальных параметров:
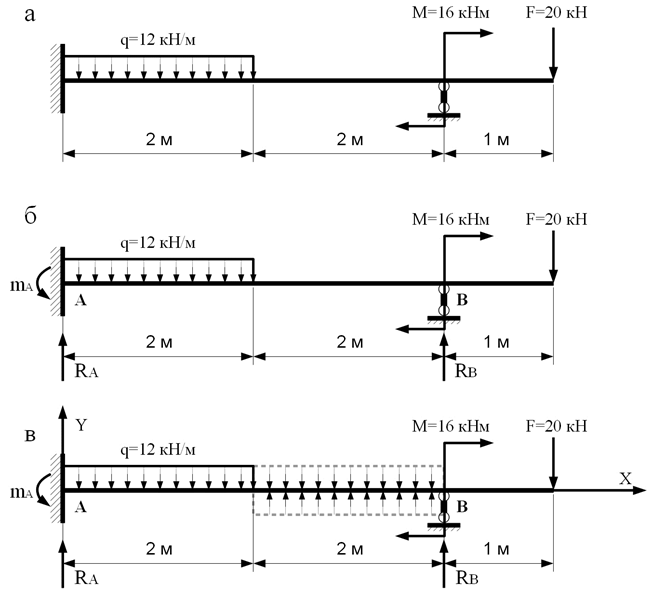
Рисунок 2 – К расчету балки
Используем данное уравнение для сечения, проходящего через характерную точку В, где прогиб над опорой равен нулю (y в = 0). Начало координатной оси х (рисунок 2в) располагаем в точке защемления балки (точка А), где прогиб и угол поворота сечения балки (начальные параметры y 0 и 0) будут также равны нулю. При этом следует учитывать все сосредоточенные и распределенные нагрузки (включая и опорные реакции), приложенные к балке слева от рассматриваемого сечения (точка В) с координатой х В. Привязка этих нагрузок к сечению осуществляет с учетом расстояний l M , l F и l q (уравнение 3). Это расстояние от начала координат до сечения, в котором приложена соответствующая сосредоточенная нагрузка или начинается действие распределенной нагрузки.
Если распределенная нагрузка не доходит до рассматриваемого сечения, то ее следует продолжать до этого сечения и, одновременно с этим, на длине добавленного участка приложить распределенную нагрузку той же величины, но обратного знака (пунктирное изображение распределенной нагрузки на рисунке 2в. Нагрузки, приложенные правее рассматриваемого сечения, не учитываются.
Положительные знаки перед составляющими уравнения (3) принимаются при условии, если воздействие от нагрузки, приводит к растяжению нижних волокон балки.
32![]() (4)
(4)
Совместно решая уравнения (2) и (4), получаем:
![]()
Знак минус момента заделки означает, что реальное направление момента защемления, в отличие от ранее принятого, осуществляется по часовой стрелке. В дальнейших расчетах будем принимать именно такое направление момента заделки.
Подставляя полученные значения ив уравнение (1), получаем
![]()
Проведем проверку полученных результатов:
Следовательно, реакции (опорные связи) определены верно.
3. По условию задачи необходимо провести повторное раскрытие статической неопределимости балки, используя метод сил.
Согласно этому методу необходимо от заданной системы балки (рисунок 2а) перейти к основной системе. Для этого отбросим шарнирную опору В и приложим в этом сечении неизвестную силу (рисунок 3). Для ее определения составим каноническое уравнение:
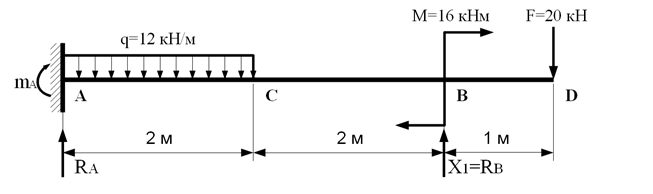
Рисунок 3 – Основная система балки
Для определения перемещенияточки приложения силыпо направлению действия неизвестной силы и перемещенияв той же точке от действия заданной нагрузки предварительно построим эпюры изгибающих моментов в основной системе при грузовом и единичном состояниях. Грузовое состояние основной системы рассмотрим методом расслоения, т.е. для каждой внешней нагрузки отдельно построим эпюры изгибающих моментов. При этом на рисунках совмещаем внешнюю нагрузку с ее эпюрой изгибающего момента (рисунок 4).
Для силы
Для внешнего момента :
Для распределенной нагрузки :
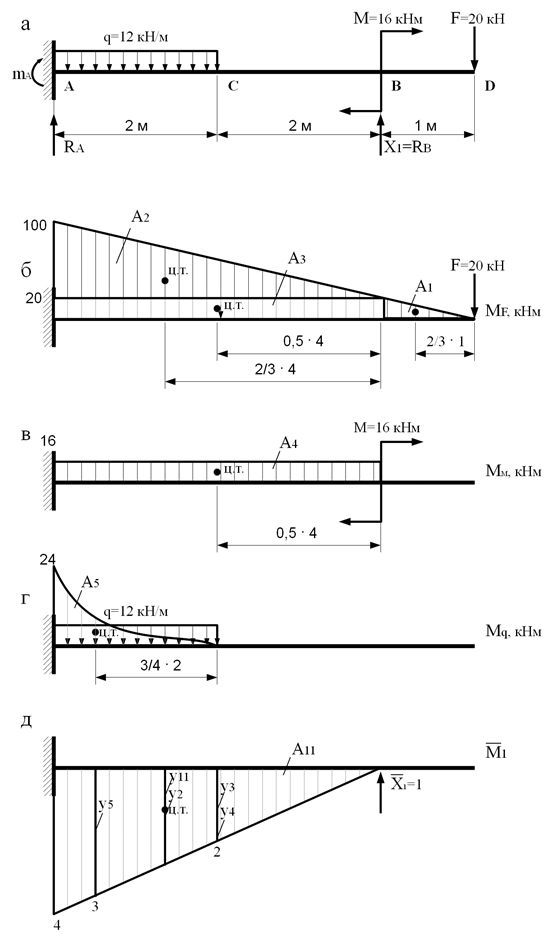
Рисунок 4 – Схема расслоения эпюр
,
,![]()
Эпюра единичного состояния представлена на рисунке 4д.
Перемещение определяем по правилу Верещагина, «перемножая» эпюры внешних и единичной нагрузок:
![]()
где площадь эпюры внешней нагрузки;
ордината единичной эпюры под центром тяжести
(Ц.Т.) эпюры от внешней нагрузки.
Для каждой эпюры внешних нагрузок () определим значения их площадей (и положения центров тяжести (Ц.Т.) (рисунки 4б, 4в, 4г).
Сведения о площадях и координатах центра тяжести простых эпюр (фигур) даны в таблице 2.
Таблица 2 – Площади и координаты их центров тяжести
|
Схема балки и нагрузки, характер эпюры |
|||
|
|
|
| |
|
Площадь эпюры и координата ее центра тяжести |
|||
|
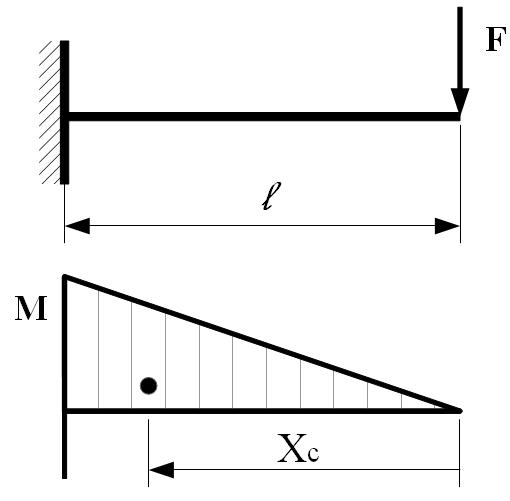
M=F ∙ l A=1/2 ∙ M ∙ l = =(F ∙ l 2)/2 X C =2/3 ∙ l |
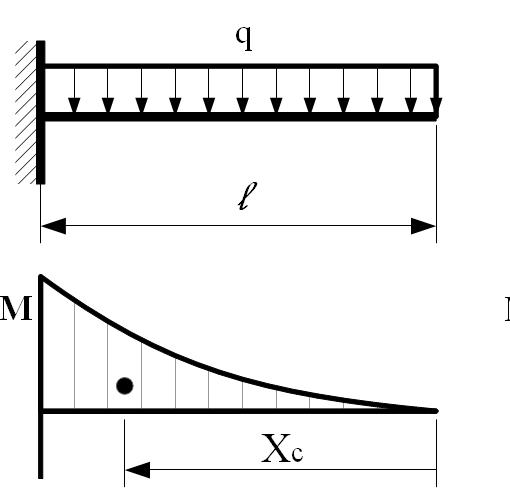
M=(q ∙ l 2)/2 A=1/3 ∙ M ∙ l = =(q ∙ l 3)/6 X C =3/4 ∙ l |
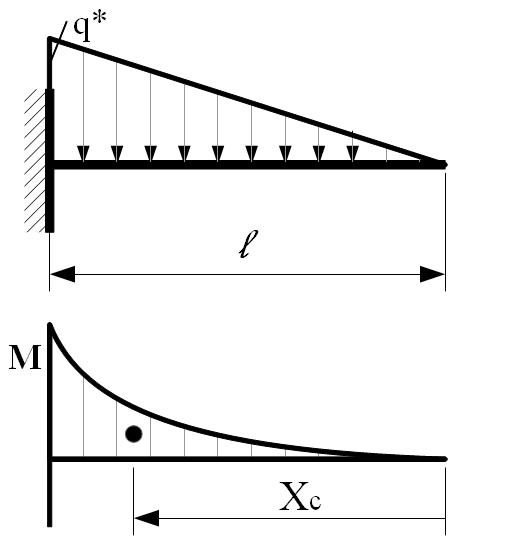
M=(q* ∙ l 2)/6 A=1/4 ∙ M ∙ l = =(q* ∙ l 3)/24 X C =4/5 ∙ l |
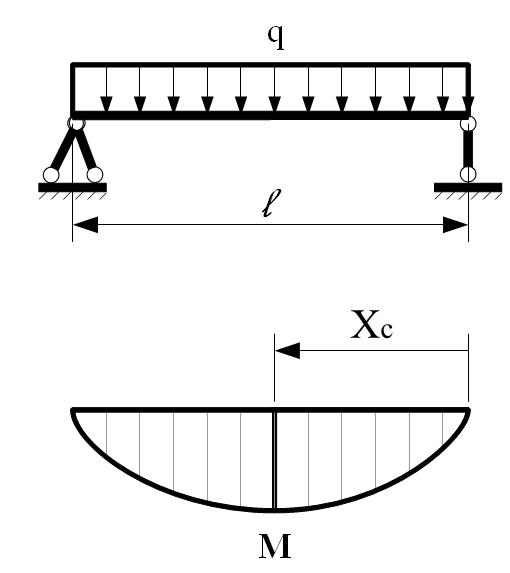
M=(q ∙ l 2)/8 A=2/3 ∙ M ∙ l = =(q ∙ l 3)/12 X C =1/2 ∙ l |
При этом площадь эпюры разбиваем на три составляющие (положения точки В:
![]()
![]()
![]() ,
,
Ординаты единичной эпюры на уровне центров тяжести эпюр внешних нагрузок указаны на рисунке 4д. Они вычислены как произведение единичной силы на расстояние от нее до рассматриваемого центра тяжести:
![]() ,
,
![]() ,
,
![]() .
.
Точно так же вычислим значения единичных моментов в серединах участков балки.
Участок BD: 1 =0, участок BC: 1 = , участокAC: 1 =
Эти значения будут необходимы для дальнейших расчетов.
Напомним, что результат «перемножения» однозначных эпюр является положительным, а разнозначных – отрицательным.
Перемещение определяем «перемножая» эпюру(рисунок 4д) саму на себя:
![]() ,
,
где А 11 – площадь единичной эпюры;
y 11 – ордината единичной эпюры на уровне ее центра тяжести.
![]() .
.
Из уравнения
Полученное значение совпадает с величиной опорной реакции, определенной с применением метода начальных параметров.
4. Для построения эпюр поперечных сил изгибающих моментовсоставим их уравнения по участкам балки (рисунок 5).
Участок 1 (): 0;
![]()
При = 0,при= 1м,
Участок 2 (ВС): 1м
при= 2 м (середина участка)
Участок 3 (СА): 3м;
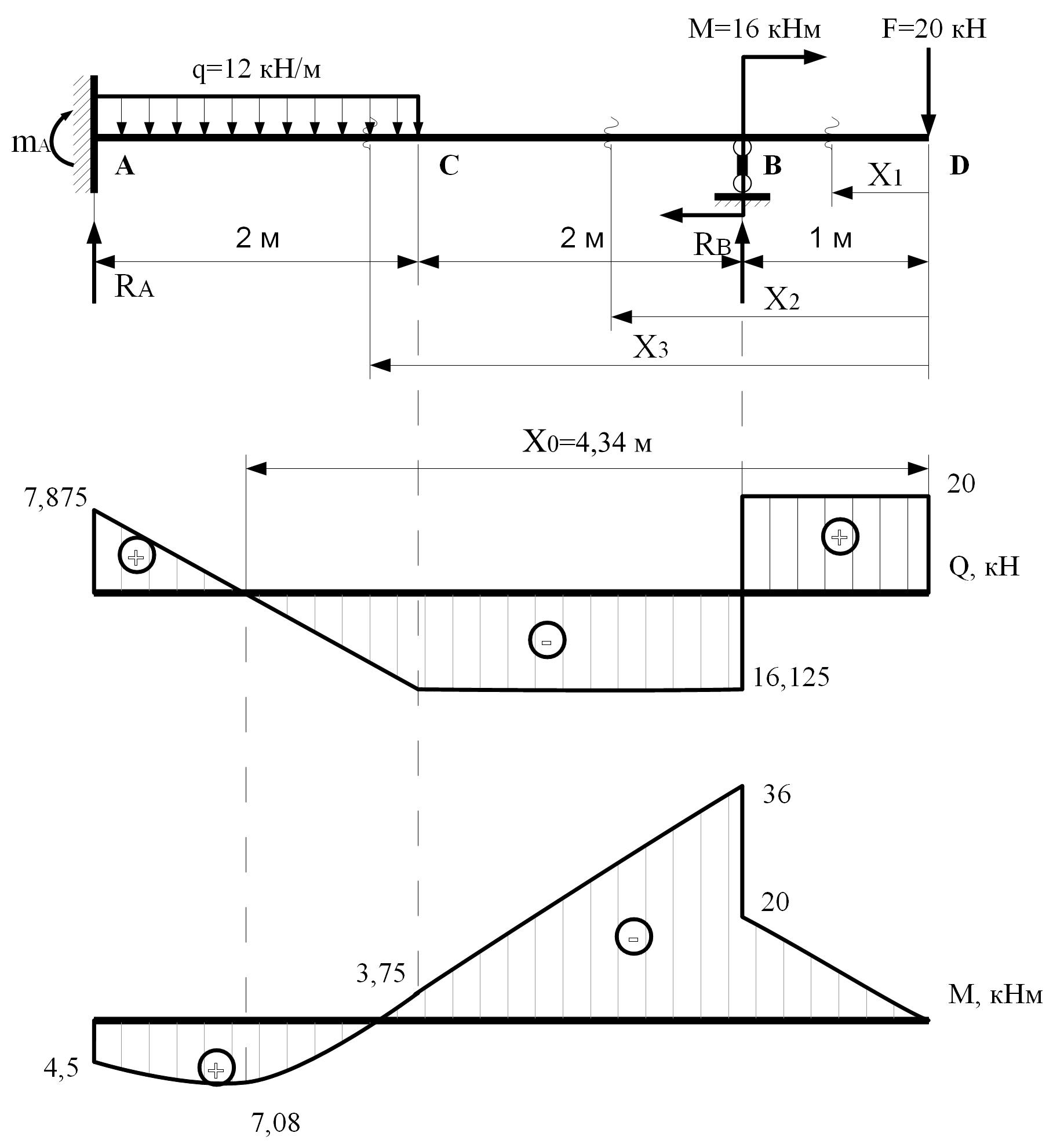
Рисунок 5 – Расчетная схема балки и эпюры Q и M