Если однородный стержень подвергается простому растяжению, то при удлинении стержня силы, приложенные к его концам, совершат некоторую работу.

Таким образом, если на элемент стержня, показанный на рис. 130, действует лишь одно нормальное напряжение то соответствующая сила совершает работу на перемещении

Зависимость между этими двумя величинами в процессе нагружения изображается прямой линией ОА на рис. а работа, совершенная в процессе деформации, определяется площадью треугольника . Обозначая эту работу через имеем

Очевидно, что такая же работа совершается во всех подобных элементах, если они имеют тот же объем. А теперь зададимся вопросом: что стало с этой работой, в какой вид или виды энергии она перешла?

Адиабатическое сжатие газа вызывает повышение его температуры. Когда адиабатически сжимается обычный стальной стержень, происходит аналогичное, очень малое повышение температуры. Начальная температура может быть восстановлена затем путем отнятия тепла. Такое изменение температуры изменяет и деформацию, однако это изменение касается очень малой доли адиабатической деформации. Если бы это было не так, то между адиабатическим и изотермическим модулями упругости наблюдалось бы значительное различие. В действительности это различие для обычных металлов очень мало. Например, адиабатический модуль Юнга для железа превышает изотермический модуль всего на 0,26%. Такого рода различиями мы будем здесь пренебрегать. Работа, затраченная на деформацию элемента, переходит в накапливаемую в нем энергию, называемую энергией деформации. При этом предполагается, что элемент остается упругим и не образуется кинетическая энергия.

Те же соображения используются и в том случае, когда на элемент действуют все шесть компонент напряжения (рис. 3). Сохранение энергии требует, чтобы работа зависела только от конечных значений, но не от порядка, в котором прикладываются силы. В противном случае, производя нагружение в одном порядке, а разгрузку - в другом, мы могли бы получить большее количество работы. Следовательно, при полном цикле деформирования из элемента можно было бы извлечь некоторую величину работы.

Определение совершенной работы проще всего произвести, если силы или напряжения возрастают одновременно в одном и том же отношении. Тогда зависимость между каждой силой и соответствующим ей перемещением остается линейной, как показано на рис. 130, б, и работа, совершенная этими силами, равна

Таким образом, представляет собой суммарную работу, приходящуюся на единицу объема, или энергию деформации в единице объема.

В предыдущих рассуждениях напряжения на противоположных гранях элемента считались равными и предполагалось, что объемных сил нет. Рассмотрим теперь работу, совершенную над элементом, когда напряжения по

объему тела изменяются и имеются объемные силы. Рассмотрим сначала усилие на грани 1 элемента (рис. 130, а); оно совершает работу на перемещении и этой грани, и величина этой работы равна где индекс 1 показывает, что функции и и должны определяться в точке . Сила на грани 2 совершает работу . Полная работа на обеих гранях

в пределе будет равна

Вычисляя работу, совершенную касательными напряжениями на гранях 1 и 2 и складывая ее с работой, определяемой выражением (г), находим работу, совершенную на обеих гранях всеми тремя компонентами напряжения:

где - компоненты перемещения в направлениях Подобным же образом может быть определена работа, совершенная на двух других парах граней. Для полной работы, совершенной напряжениями на всех этих гранях, получаем выражение

При нагружении тела объемные силы и прочие совершают работу

Полная работа, совершенная над элементом, представляется суммой работ Выполняя в (д) дифференцирование, находим для этой полной работы выражение

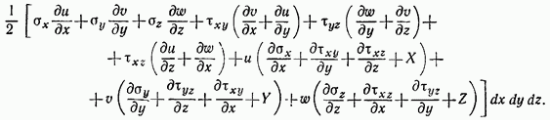
Согласно уравнениям равновесия (123), выведенным в § 84, множители в скобках при равны нулю. Величины, умножаемые на компоненты напряжения, согласно формулам (2), равны соответственно. Следовательно, полная работа, совершенная над элементом, сводится к значению, определяемому выражениями (б) и (в). Таким образом, эти формулы будут определять работу, совершенную над элементом упругого тела, или энергию, накопленную им, и в том случае, когда напряжения распределены по телу неоднородно и имеются объемные силы.

С помощью закона Гука (см. равенства (3) и (6)) мы можем выразить функцию определяемую равенством (в), как функцию одних только компонент напряжения:

Легко проверить, что

где -инварианты напряжения, введенные в § 79.

Поступая несколько иначе, мы можем использовать соотношения (11) и выразить как функцию одних только компонент деформации. Тогда

Формула (132) непосредственно показывает, что величина всегда положительна.

Легко показать, что производная от функции , определяемой формулой (132), по любой компоненте деформации дает соответствующую компоненту напряжения. Так, например, взяв производную по и используя первое из соотношений (11), находим, что

Для случая плоского напряженного состояния, в котором выражение (131) принимает вид

или через компоненты деформации

Полная энергия диформации V деформируемого упругого тела получается из энергии деформации в единице объема путем интегрирования. Обозначая элемент объема через получаем

Эта формула определяет полную работу по преодолению сопротивления внутренних сил, совершенную при нагружении. Если мы представим себе тело как совокупность очень большого числа частиц, соединенных пружинами, то эта формула будет представлять работу, совершаемую при растяжении и сжатии пружин. Для получения работы, которую совершили над частицами тела внутренние силы, нужно поменять знак на обратный.

Величина энергии деформации, накопленной в единице объема материала, иногда используется как критерий для определения предельного напряжения,

при котором происходит разрушение Чтобы согласовать теорию с тем фактом, что изотропные материалы могут выдерживать очень большие гидростатические давления без возникновения течения, было предложено разделить энергию деформации на две части, одна из которых связана с изменениями объема, а другая - со сдвигами, и считать, что прочность определяется лишь второй частью энергии 2).

Мы знаем, что изменение объема пропорционально сумме трех нормальных компонент напряжения (см. формулу (8)), так что если эта сумма равна нулю, то деформация связана только с изменением формы. Каждую компоненту напряжения можно разложить на две части

Поскольку отсюда

напряженное состояние вызывает только формоизменение, а изменение объема зависит лишь от величины равномерного растяжения Часть полной энергии, связанная с этим изменением объема, согласно формуле (8), равна

Вычитая это выражение из (131) и используя тождество

мы можем представить ту часть полной энергии, которая связана с формоизменением, в виде

В случае простого растяжения в направлении х отлична от нуля только величина и энергия формоизменения (136) равна . В случае чистого сдвига, скажем, между плоскостями от нуля отлична только - компонента и энергия формоизменения равна Если верно, что при любой системе напряжений разрушение происходит тогда, когда энергия формоизменения достигает определенного предела (характерного для материала),

то отношение между критическим значением самого по себе растягивающего напряжения и самого по себе касательного напряжения находятся из уравнения

Эксперименты со сталью показывают, что отношение между пределом текучести на растяжение и пределом текучести на сдвиг находится в очень хорошем согласии с уравнением Вводя в рассмотрение энергию деформации, можно связать принцип Сен-Венана (см. стр. 57) с накоплением энергии. Этот принцип эквивалентен утверждению, что самоуравновешенное распределение усилий на малой части упругого тела вызывает лишь местные напряжения.

При таком распределении приложенные усилия совершают работу лишь за счет деформации нагруженной области. Зафиксируем положение и ориентацию некоторого поверхностного элемента этой области. Если обозначить через порядок величины (например, среднее значение) силы, действующей на единицу площади, а через а - характерный линейный размер (например, диаметр) нагруженной части, то компоненты деформации будут иметь порядок а относительные перемещения в пределах нагруженной части будут порядка Совершенная работа будет иметь порядок или

С другой стороны, компоненты напряжения порядка вызывают энергию в единице объема порядка Следовательно, в соответствии с формулировкой принципа совершенная работа достаточна лишь для объема порядка

Здесь предполагалось, что тело имеет строго заданную форму и следует закону Гука. Последнее ограничение можно снять, если считать, что Е в вышеприведенных рассуждениях определяет просто порядок величины наклона кривых напряжения - деформация для рассматриваемого материала. Если тело не является существенно трехмерным, как это имеет место, например, в случае балки с очень тонкой стенкой или тонкой цилиндрической оболочки, то самоуравновешенное распределение усилий на одном конце может передаваться на расстояния, во много раз превышающие высоту балки или диаметр оболочки 3).

Приведенные выше рассуждения можно без изменения повторить для нагрузки с ненулевой результирующей, если в пределах нагруженной части или вблизи нее имеется закрепленный элемент поверхности. Таким образом, если деформируемый материал скреплен с абсолютно твердым, то давление, приложенное к малой части первого материала вблизи закрепления вызовет лишь местные напряжения.

Рассмотрим вначале элементарный объем dV=dxdydz в условиях одноосного напряженного состояния (рис. 1). Мысленно закрепим площадку х=0 (рис. 3). На противоположную площадку действует сила . Эта сила совершает работу на перемещении . При увеличении напряжения от нулевого уровня до значения соответствующая деформация в силу закона Гука также увеличивается от нуля до значения , а работа пропорциональна заштрихованной на рис. 4 площади: . Если пренебречь кинетической энергией и потерями, связанными с тепловыми, электромагнитными и другими явлениями, то в силу закона сохранения энергии совершаемая работа перейдет в потенциальную энергию, накапливаемую в процессе деформирования: . Величина Ф=dU / dV называется удельной потенциальной энергией деформации, имеющей смысл потенциальной энергии, накопленной в единице объема тела. В случае одноосного напряженного состояния

Рис.3. Расчетная схема энергии деформации

Рис.4. Линейный закон сопротивления

При одновременном действии напряжений , и на главных площадках (т. е. при отсутствии касательных напряжений) потенциальная энергия равна сумме работ, совершаемых силами на соответствующих перемещениях . Удельная потенциальная энергия равна

Рис.5. Расчетная схема сдвигаемой энергии

В частном случае чистого сдвига в плоскости Оху, изображенном на рис. 5, сила совершает работу на перемещении . Соответствующая этому случаю удельная потенциальная энергия деформации равна

Подобные соотношения будут иметь место при сдвиге в других плоскостях.

В общем случае напряженно-деформированного состояния будем иметь

Выразив напряжения через деформации с использованием соотношений (6) и (10), получим еще одну форму записи для Ф - через компоненты тензора деформаций

Еще одну форму записи для удельной потенциальной энергии деформации получим, разложив тензоры напряжений и деформаций на шаровые тензоры и девиаторы. В результате (11) можно привести к одной из форм

(13)

Здесь введены обозначения для - интенсивности касательных напряжений и - интенсивности деформаций сдвига, которые выражаются через вторые инварианты и девиаторов тензора напряжений и тензора деформаций следующим образом:

Первые слагаемые в (13) соответствуют произведению шаровых составляющих тензоров напряжений и деформаций, а вторые - произведению девиаторных составляющих. Так как шаровой тензор характеризует изменение объема, а девиатор - изменение формы, то соотношения (13) можно интерпретировать как разложение удельной потенциальной энергии на две составляющие: Ф=Ф 0 +Ф ф , где Ф 0 соответствует изменению объема без изменения формы, а Ф ф - изменению формы без изменения объема. Первая составляющая будет вычисляться через компоненты тензора напряжений следующим образом:

(14)

Удельную потенциальную энергию изменения формы проще найти не через интенсивность касательных напряжений, а как разностьФ - Ф 0 . Вычитая (14) из (12), после преобразований получим

Лекция № 9. Механические характеристики конструкционных материалов

Механические характеристики определяются следующими факторами:

• веществом, его структурой и свойствами;
• конструктивными особенностями элемента, т. е, размерами, формой, наличием концетраторов, состоянием поверхности;
• условиями при нагружении: температурой, скоростью, повторяемостью нагрузки и др.

Конструкционные материалы в процессе деформирования вплоть до разрушения ведут себя по разному. Пластичное поведение характеризуется существенным изменением формы и размеров, при этом к моменту разрушения развиваются значительные деформации, не исчезающие после снятия нагрузки. Такие материалы называют пластичными. При хрупком поведении разрушение наступает при весьма малых деформациях, и материалы с такими свойствами называют хрупкими. Однако одни и те же конструкционные материалы, находящиеся в различных условиях деформирования, ведут себя по разному: при одних условиях проявляют себя как пластичные материалы, при других-как хрупкие. В связи с этим, основные макромеханические характеристики материалов - упругость, пластичность, вязкость и др. правильнее относить не к их свойствам, а к состояниям материала.

Потенциальная энергия деформации

Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу А на соответству­ющих перемещениях. Одновременно с этим в упругом теле накап­ливается потенциальная энергия его деформирования U . При дей­ствии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:

А = U + K. (2.8)

При действии статических нагрузок К = 0, следовательно,

А = U. (2.9)

Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформа­ции. При разгрузке тела производится работа за счет потенциаль­ной энергии деформации, накопленной телом. Таким образом, уп­ругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в технике, например, в заводных пружи­нах часовых механизмов, в амортизирующих рессорах и др. В слу­чае простого растяжения (сжатия) для вывода необходимых расчет­ных зависимостей потенциальной энергии деформации рассмотрим решение следующей задачи.

На рис. 2.4, а изображен растягиваемый силой Р стержень, удлинение которого соответствует отрезку Dl , ниже показан график изменения величины удлинения стержня Dl в зависимости от силы Р (рис. 2.4, б ). В соответствии с законом Гука этот график носит линейный характер.

Пусть некоторому значению силы Р соответствует удлинение стержня Dl. Дадим некоторое приращение силе DР - соответству­ющее приращение удлинения составит d (Dl ). Тогда элементарная работа на этом приращении удлинения составит:

dA = (P + d P )×d (D l ) = P ×d (D l ) + d P × d (D l ) , (2.10)

вторым слагаемым, в силу его малости, можно пренебречь, и тогда

dA = P ×d (D l ). (2.11)

Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка - перемещение”, работа внешней силы Р на перемещении Dl будет равна площади треугольника ОСВ (рис. 2.4), т.е.

А = 0,5 Р ×Dl . (2.12)

В свою очередь, когда напряжения s и деформации e распреде­лены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:

Поскольку, в данном случае имеем, что V = F l , P = s F иs = Е e,то

т.е. подтверждена справедливость (2.9).

С учетом (2.5) для однородного стержня с постоянным попе­речным сечением и при Р = const из (2.14) получим:

2.5. Статически определимые и статически
неопределимые системы

Если при рассмотрении заданной системы, находящейся в рав­новесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления, а также внутренние усилия в ее эле­ментах, можно определить только по методу сечений, без использо­вания дополнительных условий, то такая система называется ста­тически определимой .

Сопоставление предела прочности хрупких материалов при растяжении с пределом прочности при сжатии показывают, что эти материалы обладают, как правило, более высокими прочностными показателями при сжатии, нежели при растяжении. Величина отношения для чугуна составляет 0.2 ¸0.4, для керамических материалов 0.1¸0.2. Для пластичных материалов установлено, что .

Большое влияние на проявление свойств материалов оказывает скорость нагружения и температурное воздействие. При высокоскоростном нагружении более резко проявляются свойства хрупкости, а при медленном нагружении - свойства пластичности. Например, хрупкое стекло способно при длительном воздействии нагрузки в условиях нормальной температуры (+20 о С) проявляет пластические свойства. Пластичные же материалы, такие, как малоуглеродистая сталь, при воздействии ударных нагрузок проявляет хрупкие свойства. В зависимости от указанных обстоятельств механические свойства материалов проявляются по-разному. Обобщенный анализ свойств материалов с учетом температуры и времени оказывается очень сложным. Функциональная зависимость между четырьмя параметрами s, e, температурой t o и временем t, т.е. не является адекватной и содержит в сложной форме дифференциальные и интегральные соотношения, входящих в нее величин.

Так как в обобщенной форме, точное аналитическое выражение функции f получить невозможно, то влияние температуры и фактора времени рассматривается в настоящее время применительно только к частным классам задач. Деление на классы производится как по характеру действия внешних сил так и по типу материалов, а также в зависимости от скорости нагружения.

Наиболее, изучаемыми в механике материалов, являются процессы происходящие при действии медленно изменяющихся (статических) нагрузок.

Скорость изменения этих нагрузок во времени настолько мала, что кинетическая энергия деформируемого тела, составляет незначительную долю от работы внешних сил. Поэтому работа внешних сил превращается только в упругую энергию и в необратимую тепловую энергию, связанную с пластическими деформациями тела.

При статических испытаниях материалов в различных температурных режимах определяется зависимость механических характеристик материалов от температуры. Эта зависимость характеризует изменения внутрикристаллических и межкристаллических связей, а в некоторых случаях и структурными изменениями материалов. В общем случае с ростом температуры, прочностные характеристики материалов существенно падают. При этом, чем выше температура, тем труднее определить механические характеристики материалов. Происходит это не только потому, что возрастают сложности в технике эксперимента, но также вследствие того, что сама характеристика становится менее определенной.

При статическом нагружении, начиная с некоторых значений температур, фактор времени становится очень существенным. Для разных материалов это явление происходит при совершенно различных температурных режимах. Влияние фактора времени обнаруживается и при нормальных температурах. Для металлов его влияние, из-за незначительности, можно пренебречь. А для органических материалов даже при низких температурах время нагружения имеет существенное значения.

В заключение отметим наиболее важные свойства материалов которые обнаруживаются при их испытаниях. Эти свойства имеют фундаментальное значение при построении физических уравнений механики твердого деформируемого тела.

Упругость - это способность твердого деформируемого тела восстанавливать свою форму и объем после прекращения действия внешних нагрузок.

Пластичность - это свойство твердого деформируемого тела до разрушения необратимо изменять свою форму и объем от действия внешних сил.

Вязкость - это свойство оказывать сопротивление за счет трения происходящего при перемещении элементарных частиц тела относительно друг друга в процессе деформирования. Отметим, что при этом, как показывают результаты экспериментов, сила сопротивления, возникающая за счет внутреннего трения материалов, прямым образом зависит от величины скорости перемещения элементарных частиц относительно друг друга.

Упругость, пластичность и вязкость являются главными физическими свойствами твердого деформируемого тела.

Ползучесть - это явление характеризующееся изменения во времени величин деформаций и напряжений в теле при действии статических нагрузок.

Выносливость - при действии периодически изменяющихся по времени нагрузок, это явление, которое характеризуется чувствительностью и изменениями прочностных свойств материалов в зависимости от числа циклов нагружения.

В реальной практике встречаются такие конструкции при рас­чете которых одних лишь уравнений равновесия оказывается не­достаточно, в связи с чем требуется формулирование дополнитель­ных уравнений, связанных с условиями деформирования конструк­ции.

Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми .

По сравнению со статически определимыми системами, в ста­тически неопределимых системах имеются дополнительные связи, которые называются лишними .

Термин “лишние связи” является условным. Эти связи являют­ся лишними с точки зрения расчетных предпосылок. В действи­тельности эти связи создают дополнительные резервы для конст­рукций, как в плане обеспечения её жесткости, так и прочности.

На рис. 2.5, а изображен кронштейн, состоящий из двух стерж­ней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р , а система яв­ляется плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла А , т.е.

åx = 0, åy = 0. (2.16)

Раскрывая эти уравнения, получаем замкнутую систему линей­ных уравнений относительно неизвестных усилий N 1 и N 2 в кото­рой количество уравнений равно количеству неизвестных:

-N 1 - N 2 sin a = 0; -N 2 cos a - Р = 0.

Если конструкцию крон­штейна усложнить, добавив еще один стержень (рис. 2.5, б ), то усилия в стержнях N 1 , N 2 и N 3 прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.16) имеются уже три неиз­вестных усилия в стержнях. В таких случаях говорят, что сис­тема один раз статически неопределима. Разность между числом неизвестных усилий и количеством независимых (значащих) урав­нений равновесия, связывающих эти усилия, называется сте­пенью статической неопределимости рассматриваемой системы.

В общем случае под n -раз статически неопределимой системой понимается система, в которой число неизвестных внешних опорных реакций и внутренних усилий превышает число не­зависимых и значащих уравнений равновесия на n единиц.

Рассмотрим более подробно особенности напряженного состоя­ния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, со­ставляющей угол a с плоскостью нормального сечения (рис. 2.6, а ).

Из условия åz = 0, записанного для отсеченной части стержня (рис. 2.6, б ), получим:

р F a = s F , (2.17)

где F - площадь поперечного сечения стержня, F a = F /cos a - пло­щадь наклонного сечения. Из (2.17) легко установить:

р = s сos a. (2.18)

Раскладывая напряжение р по нормали и касательной к на­клонной площадке (рис. 2.6, в ), с учетом (2.18) получим:

s a = p cos a = s cos 2 a; t a = p sin a = s sin 2 a . (2.19)

Полученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, про­ходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла a. При a = 0 из (2.19) следует, что s a = s, t a = 0. При a = , т.е. на продольных площадках, s a = t a = 0. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения t a принимают наибольшие зна­чения при a = , и их величина составляет t max = . Важно отме­тить, как это следует из (2.19), что . Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряже­ния равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит назва­ние закона парности касательных напряжений .

Теперь перейдем к анализу деформаций в растянутом стержне. Наблюдения показывают, что его удлинение в продольном направ­лении сопровождается пропорциональным уменьшением попереч­ных размеров стержня (рис. 2.7).

Если обозначить:

E прод = ; e попер = - , m = - ,

то, как показывают эксперименты, m = const для данного материала и является безразмерным коэффициентом Пуассона . Вели­чина m является важной характеристикой материала и определяется экспериментально. Для реальных материалов m принимает значе­ния 0,1 ¸ 0,45.

При растяжении стержня возникают не только линейные, но и угловые деформации.

Рассмотрим прямой угол АВС (рис. 2.8, а ), образованный отрез­ками АВ и АС , в недеформированном состоянии.

При растяжении стержня точки А, В и С займут положение А ¢, B ¢, C ¢ соответственно. Величина

g a = ÐВАС - ÐА ¢B ¢C ¢

называется угловой деформацией или угловым сдвигом в точке А .

Совместим точки А и А ¢ и рассмотрим взаимное расположение отрезков АВ и А ¢B ¢(рис. 2.8, б ). На этом рисунке отметим вспомо­гательные точки K и L и прямую n , перпендикулярную отрезку А ¢B ¢. Из рис. 2.8, б имеем:

e прод = ; e попер = ,

откуда с учетом e прод = получим:

Рис. 2.9

правило, экспериментально определяют диаграмму рас­тяжения в координатах s и e (рис. 2.9), На диаграмме от­мечены характерные точки. Дадим их определение.

Наибольшее напряже­ние, до которого материал следует закону Гука, назы­вается пределом про­порциональности s П . В пределах закона Гука тангенс угла наклона прямой s = f (e) к оси e определяется величиной Е .

Упругие свойства материала сохраняются до напряжения s У , называемого пределом упругости . Под пределом упругости s У понимается такое наибольшее напряжение, до которого матери­ал не получает остаточных деформаций, т.е. после полной разгруз­ки последняя точка диаграммы совпадает с начальной точкой 0.

Величина s Т называется пределом текучести материала. Под пределом текучести понимается то напряжение, при котором происходит рост деформаций без заметного увеличения нагрузки. Если необходимо различать предел текучести при растяжении и сжатии s Т соответственно заменяется на s ТР и s ТС . При напряже­ниях больших s Т в теле конструкции развиваются пластические деформации e П , которые не исчезают при снятии нагрузки.

Отношение максимальной силы, которую способен выдержать образец, к его начальной площади поперечного сечения носит на­звание предела прочности, или временного сопротивления, и обоз­начается через, s ВР (при сжатии s ВС ).

В табл. 2 приводятся значения указанных характеристик (в кН/м 2) наиболее распространенных конструкционных матери­алов.

Таблица 2

При выполнении практических расчетов реальную диаграмму (рис. 2.9) упрощают, и с этой целью применяются различные ап­проксимирующие диаграммы. Для решения задач с учетом упру­го-пластических свойств материалов конструкций чаще всего применяется диаграмма Прандтля . По этой диаграмме на­пряжение изменяется от нуля до предела текучести по закону Гука s = Е e, а далее при росте e, s = s Т (рис. 2.10).

Способность материалов получать остаточные деформации но­сит название пластичности . На рис. 2.9 была представлена ха­рактерная диаграмма для пластических материалов.

Рис. 2.10 Рис. 2.11

Противоположным свойству пластичности является свойство хрупкости , т.е. способность материала разрушаться без образова­ния заметных остаточных деформаций. Материал, обладающий этим свойством, называется хрупким . К хрупким материалам относятся чугун, высокоуглеродистая сталь, стекло, кирпич, бетон, природные камни. Характерная диаграмма деформации хрупких материалов изображена на рис. 2.11.

Энергия упругой деформации

Наименование параметра	Значение
Тема статьи:	Энергия упругой деформации
Рубрика (тематическая категория)	Механика

Упруго деформированное тело, к примеру, растянутый или сжатый стержень, возвращаясь в недеформированное состояние, может, подобно сжатой или растянутой пружинœе, совершить работу над внешними телами, т. е. обладает некоторым запасом энергии. Поскольку эта энергия обусловлена взаимным расположением элементов тела, она представляет собой потенциальную энергию. Запас энергии деформированного тела равен, очевидно, работе, которая совершается внешними силами при деформации.

Вычислим энергию упруго растянутого (сжатого) стержня. При растяжении на стержень крайне важно действовать силой, величина которой определяется выраже­нием (113). Работа этой силы равна

где буквой х обозначено абсолютное удлинœение стержня, ĸᴏᴛᴏᴩᴏᴇ в процессе деформации изменяется от 0 до Δl. Сила f , соответствующая удлинœению х, согласно (113) равна

Следовательно,

Умножая числитель и знаменатель полученного выражения на l , заменяя затем отношение Δl/l относительным удлинœением ε и учитывая, наконец, что Sl дает объём стержня V, получим:

(121)

Введем в рассмотрение плотность энергии u, которую определим как отношение энергии ΔU к тому объёму ΔV, в котором она заключена:

Поскольку в нашем случае стержень однороден и деформация является равномерной, т. е. одинаковой в разных точках стержня, энергия (121) распределœена в стержне также равномерно с постоянной плотностью. По этой причине можно считать:

(122)

Выражение (122) дает плотность энергии упругой деформации при растяжении (или при сжатии). Аналогичным образом можно получить, что плотность энергии упругой деформации при сдвиге равна

(123)

Энергия упругой деформации - понятие и виды. Классификация и особенности категории "Энергия упругой деформации" 2014, 2015.

-

Силы упругости, возникающие при упругой деформации, являются потенциальными. Рассмотрим пружину жесткостью k. Один ее конец закрепим, а за другой конец будем ее растягивать. По закону Гука зависимость силы упругости от величины деформации пружины имеет вид: . Эта... .

- Потенциальная энергия упругой деформации при растяжении – сжатии.

В упругой области нагружения существует прямо пропорциональная зависимость между относительной линейной деформацией и нормальным напряжением, называемым законом Гука (1756г. – Роберт Гук). &... .

- ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ

Рассмотрим вначале элементарный объем dV=dxdydz в условиях одноосного напряженного состояния (рис. 1). Мысленно закрепим площадку х=0 (рис. 3). На противоположную площадку действует сила. Эта сила совершает работу на перемещении. При увеличении напряжения от нулевого уровня до... .

- Разрушение валов из различных материалов. Потенциальная энергия упругой деформации

Характер разрушения зависит от напряжённого состояния и механических свойств материала. Из анализа формулы (7.9) видно, что касательные напряжения в плоскости поперечного сечения распределены неравномерно и достигают максимума на периферии его (рис.7.6). В элементе... .

- Потенциальная энергия упругой деформации

Как было выяснено ранее, удельная потенциальная энергия упругой деформации определяется формулой. Рассмотрим случай чистого изгиба (M = const, Q = 0). Имеет место линейное напряжённое состояние: , &...