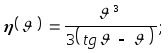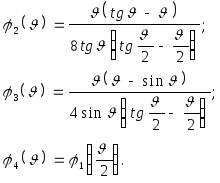Строительная механика метод перемещений примеры. Расчет конструкций методом перемещений

В методе сил за лишние неизвестные принимались усилия в «лишних» связях (силы и моменты). Определив значения «лишних» неизвестных, можно найти внутренние усилия M , Q и N в любых сечениях, а также перемещения (линейные и угловые) любой точки конструкции. В стержневой системе с учетом принятых ранее допущений и гипотез, заданной нагрузке однозначно отвечают перемещения – вспомним гипотезу о линейной связи нагрузки и перемещений.

Сформулируем следующую проблему: можно ли найти внутренние усилия по соответствующим им перемещениям и, разумеется, известной внешней нагрузке? Эта проблема обратна уже имеющемуся решению – по заданной внешней нагрузке и найденным внутренним усилиям найти перемещение искомого сечения.

Рассмотрим статически неопределимую раму (рис. 1) под действием внешней нагрузки и попытаемся установить, какие перемещения следует знать, чтобы однозначно по ним найти внутренние усилия.

Очевидно, что внешняя нагрузка вызовет изгиб и сжатие-растяжение стержней, а также повороты жестких узлов и их линейные перемещения. Если пренебречь изменением длины стержней в результате изгиба и растяжения-сжатия, то линейные смещения концов стержня будут одинаковы. Угловые перемещения концов стержней, входящих в одни жесткий узел (жестко соединенных друг с другом) также будут одинаковы. Следовательно, в незагруженных внешней нагрузкой стержнях внутренние усилия возникают в результате угловых и линейных перемещений их концов. В загруженных внешней нагрузкой стержнях к внутренним усилиям от смещения концов стержней добавляются усилия от заданной нагрузки. Когда рассматриваем расчет стержней на заданную нагрузку, то перемещения концов стержней в этом случае отсутствуют – стержни являются кинематически определимыми. Сказанное позволяет разбить задачу о расчете статически неопределимой (да и статически определимой) стержневой системы на два этапа:

1. Расчет на заданную нагрузку в предположении, что концы стержней не смещаются, т.е. расчеткинематически определимой рамы.

2. Расчет на действие, нам неизвестных , угловых и линейных перемещений концов стержней при отсутствии внешней нагрузки. Следовательно, угловые и линейные перемещения концов стержней следует принять за неизвестные.

С точки зрения неизвестных перемещений приведенная на рис. 1 рама будет трижды неопределима, или, как принято говорить – трижды кинематически неопределима, так как требуется найти угловые перемещения узлов 1 и 2, а также их линейное смещение, которое одинаково у них, так как они связаны стержнем, изменением длины которого пренебрегаем.

Итак, степень кинематической неопределимости находим по формуле:

H = n y + n л , где

n y – число жестких узлов в стержневой системе;

n л – число возможных независимых линейных смещений концов стержней.

2. Основная система метода перемещений. Канонические уравнения.

Чтобы найти решение рамы как сумму решений двух задач – кинематически определимой от внешней нагрузки и от действительных перемещений узлов, следует сформировать основную систему по некоторым универсальным правилам, а именно:

– в жесткие узлы вводятся защемления, препятствующие только их повороту;

– от линейных смещений концы стержня закрепляются одностержневыми шарнирными опорами (одна наложенная связь препятствует только одному перемещению).

Наложенные на раму связи, обеспечивающие ее кинематическую определимость, называютсяфиктивными связями .

На рис. 2 показана основная система метода перемещений для рамы, приведенной на рис. 1.

Из анализа основной системы, сформированной по определенным правилам, следует, что она представляет собой набор отдельных стержней, концы которых жестко защемлены или шарнирно оперты. Мы можем, в самом общем виде, рассчитать их на возможные случаи внешнего нагружения, используя, где надо, метод сил. Получим библиотеку решений, которую можем при необходимости расширить. Очевидно, что в таком случае расчеткинематически определимой рамы на внешнюю нагрузку будет формален, так как заключается в наборе эпюр внутренних усилий для каждого отдельного стержня по заранее известным решениям.

Второй этап решения связан с действительными перемещениями концов стержней, а они-то нам и неизвестны! Следовательно, надо найти действительные перемещения концов стержней.

Вернемся к анализу основной системы метода перемещений. Основная система отличается от заданной и нам следует сформулировать условия, при которых они будут эквивалентны. Такими условиями однозначно является отсутствие введенных «фиктивных» связей. Формулировка таких условий достигается условием равенства нулю реакций во всех введенных связях от заданной внешней нагрузки и действительных, пока неизвестных, перемещений концов стержней. Для основной системы, показанной на рис. 2, запишем:

Реакция в первой связи (реактивный момент) будет состоять:

– реакция в первой связи от действительного поворота первой фиктивной связи (узла);

– реакция в первой связи от действительного смещения второй фиктивной связи (узла);

– реакция в первой связи от действительного смещения третьей фиктивной связи (узлов 1 и 2);

– реакция в первой фиктивной связи от действия заданной нагрузки.

По аналогии с методом сил, результат действия неизвестных перемещений представим как:

r ij – реакция в i -й связи от единичного смещения j -й связи;

Z j – действительное (искомое) смещение j -й связи.

Тогда можем записать следующую систему канонических уравнений метода перемещений:

Из решения полученной системы канонических уравнений найдем искомые действительные перемещенияZ j .

Расчет статически неопределимых систем методом сил на различные воздействия сводится к определению усилий в лишних связях из системы канонических уравнений этого метода. Вычисление внутренних усилий в различных элементах сооружения и построение их эпюр в методе сил производится в основной системе, как правило, статически определимой, испытывающей заданные воздействия и воздействия усилий в лишних связях. Таким образом, выявление напряженно-деформированного состояния сооружений в расчетах методом сил начинается с получения картины распределения внутренних усилий и завершается вычислением перемещений отдельных узлов и сечений сооружения.

Возможен принципиально иной подход к расчету сооружений, когда выявление их напряженно-деформированных состояний начинается с определения перемещений от заданных воздействий и завершается построением эпюр внутренних усилий. Такой подход в расчетах сооружений реализуется в методе перемещений.

В методе перемещений сохраняются допущения, ранее принятые при расчете сооружений методом сил, а именно: материал, из которого изготовлены элементы сооружений, подчиняется закону Гука; перемещения отдельных сечений и узлов сооружений малы по сравнению с их геометрическими размерами. C учетом сформулированных допущений сооружения можно рассматривать как линейно-деформируемые системы, для которых справедлив принцип независимости действия сил и вытекающий из него принцип пропорциональности.

За неизвестные в методе перемещений принимаются перемещения узлов от заданных воздействий: линейные перемещения шарнирных и жестких узловZ 1 и Z 2 и повороты жестких узлов Z 3 (рис. 14.1,а,б). Суммарное количество неизвестных угловых (n θ) и линейных (n Δ) перемещений узлов называется степенью кинематической неопределимости сооружения.

n kin = n θ + n Δ . (14.1)

Число неизвестных угловых перемещений n θ равно количеству жестких узлов сооружения.

Для сооружений, в которых перемещения от внешних воздействий обусловлены преимущественно изгибными деформациями, при определении числа независимых линейных перемещений узлов вводятся дополнительные допущения:

1. Элементы сооружений считаются нерастяжимыми и несжимаемыми, т.е. пренебрегают изменением их длин под действием продольных сил.

2. Предполагается, что длины хорд искривленных стержней равны их первоначальным длинам, т.е. А′В′ = АВ (рис. 14.2).

Считая сформулированные допущения справедливыми, число независимых линейных перемещений узлов сооруженияn Δ можно определить по его шарнирной схеме, полученной из заданного сооружения введением во все жесткие узлы, включая и опорные, режущих цилиндрических шарниров. Степень свободы полученной таким образом шарнирной схемы будет равна числу независимых линейных перемещений узлов заданной системы. Для подсчета количества степеней свободы плоской шарнирной схемы W используют формулу:

W = 2Y − C − C o , (14.2)

где Y – число узлов; C – число стержней, соединяющих узлы;

C o – число опорных связей.

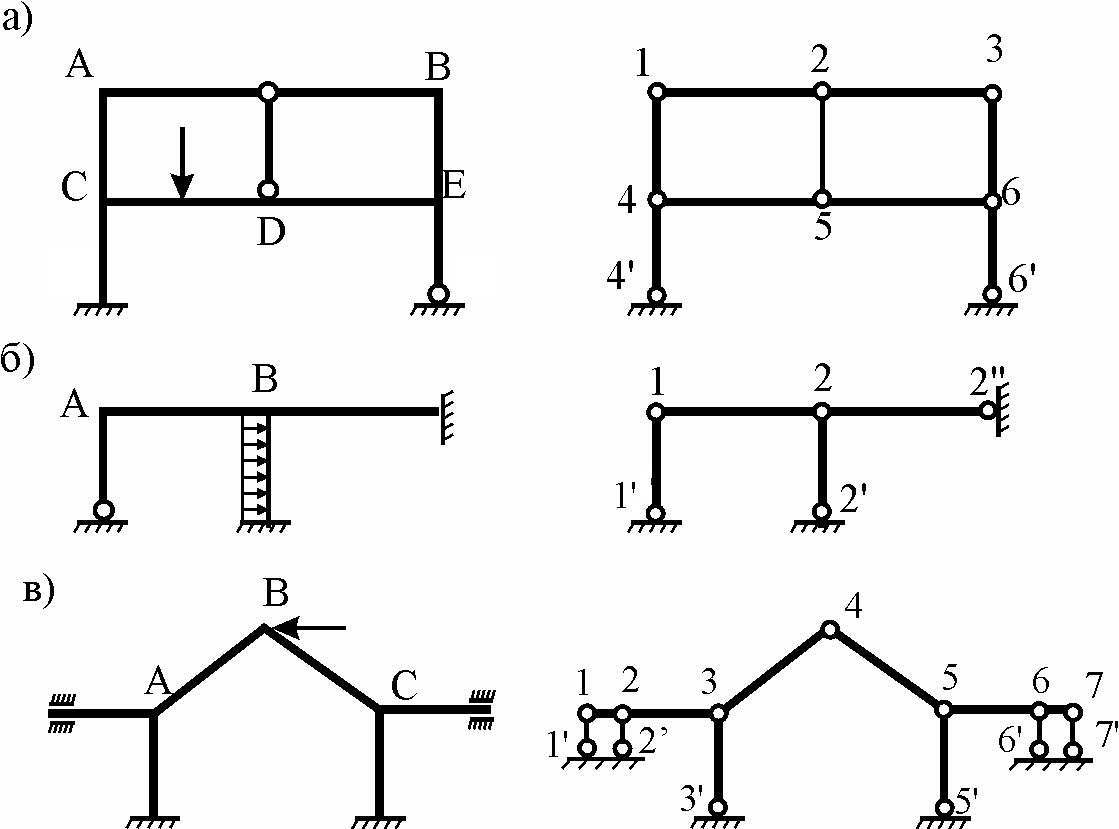
Пример 14.1.1. Определить степень кинематической неопределимости рам, показанных на рисунке 14.3.

Рис. 14.3,а: n θ = 5, так как рама имеет пять жестких узлов (А, B, C, D, E); n Δ = W = 2Y − C − C o = 2 · 6 − 7 − 2 = 3 (узлы шарнирной схемы 1 – 6; стержни, соединяющие эти узлы: 12, 23, 45, 56, 14, 25, 36; опорные связи 44′, 66′); n kin = n θ + n Δ = 5 + 3 = 8.

Рис. 14.3,б: n θ = 2 (узлы А и В); n Δ = W = 2 · 2 − 1 − 3 = 0 (узлы шарнирной схемы 1 и 2; стержень, соединяющий эти узлы 12, опорные связи 11′, 22′, 22′′); n kin = 2 + 0 = 2.

Рис. 14.3,в: n θ = 3 (узлы А, В, С); n Δ = W = 2 · 7 − 6 − 6 = 2 (узлы шарнирной схемы 1 – 7; стержни, соединяющие эти узлы 12, 23, 34, 45, 56, 67; опорные связи 11′, 22′, 33′, 55′, 66′, 77′); n kin = = 3 + 2 = 5.

В качестве неизвестных принимаются перемещения узлов конструкции. Каждый узел в общем случае имеет три возможных перемещения: линейное перемещение по горизонтали; линейное перемещение по вертикали; угловое перемещение (угол поворота) жесткого соединения стержней в узле.

Общий подсчет неизвестных ведется по формуле:

где z – общее количество неизвестных перемещений; z угл . – угловые перемещения жестких узлов конструкций; z лин . – линейные независимые перемещения всех узлов конструкции.

Если z угл . всегда равно количеству жестких узлов конструкции (на рисунке 73а один жесткий узел 1), то z лин . равно степени свободы шарнирной схемы конструкции (рамы).

Для получения шарнирной схемы рамы вводятся шарниры во все жесткие узлы рамы, включая и жесткие заделки (опоры) (рис. 73б). Для полученной рамы подсчитываем степень свободы:

Результат еще не означает, что z лин. = 0 . Необходимо провести анализ полученной конструкции. Заметим, что шарниры 0, 1, 4 лежат на одной прямой, что означает – система мгновенно изменяемая, узел 2 при этом не ликвидирует этого дефекта. Нам необходимо поставить опорный стержень по горизонтали в узел 1 или в узел 2 и тогда:

Основная система метода перемещений - единственная. Она получается путем закрепления всех возможных перемещений узлов рамы (конструкции)

введением в жесткие узлы заделки (заделки препятствуют только повороту узла) и опорных стержней по возможным перемещениям узлов шарнирной схемы конструкции.

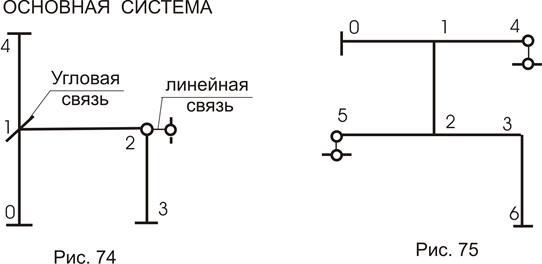
Для приведенной рамы (рис. 73) основная система показана на рис. 74. Общее число неизвестных будет равно 2 – по количеству введенных связей.

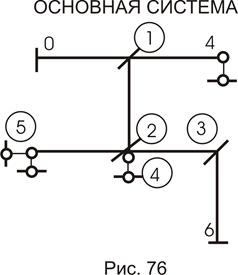
Для рамы (рис. 75) основная система приведена на рис.76. Здесь установлено три жесткие связи и две линейные в виде опорных стержней. И мы получили:

Количество введенных связей в конструкцию (раму) определяет и степень кинематической неопределимости рамы. В первом примере она равна 2, во втором – 5. В каждой введенной связи возникают реактивные усилия: в заделке - только момент (заделка не препятствует линейному смещению!), а в линейных связях - только реакция (усилие) по направлению этой связи.

Приведение основной системы к исходной производится условием:

т. е. реактивное усилие в i -ой связи равно нулю, т. к. в заданной системе этой связи нет.

По принципу независимости действия сил (воздействий) запишется:

Распишем это условие для первой приведенной конструкции (рис. 74):

Для второй конструкции (рис. 76) мы получим уже 5 уравнений по числу неизвестных перемещений. Вот одно из них (для третьей связи):

Здесь - реактивное усилие в i -ой связи от внешней нагрузки; - реактивное усилие в i -ой связи от перемещения к -ой связи.

Реакция с перемещением связана соотношением:

где - реактивное усилие в i -ой связи от перемещения к -ой связи на единицу; - истинное перемещение к -ой связи.

Подставляя последнее соотношение в условия , получаем систему канонических уравнений. Для первой конструкции (рис. 74) она запишется:

Рассчитаем раму, представленную на рисунке 77.

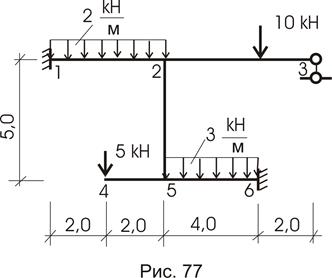
Число неизвестных:

(два жестких узла).

Линейные неизвестные определяются из шарнирной схемы рамы (рис. 78а):

Узлы 1, 2, 3 находятся на одной прямой и, если не установим недостающую связь в узел 2 по вертикали, получим мгновенно-изменяемую конструкцию. Поэтому установим в узел 2 по вертикали недостающую связь. Основная системе показана на рис. 78б (нумерация связей в кружочках) .

Система канонических уравнений запишется:

Реактивное усилие в первой связи от перемещения первой связи на единицу. Первая связь заделка. Значит она может поворачиваться. Даем ей поворот на . Произойдет деформация только тех стержней, которые составляют этот узел (рис. 78в). По деформированному состоянию строим

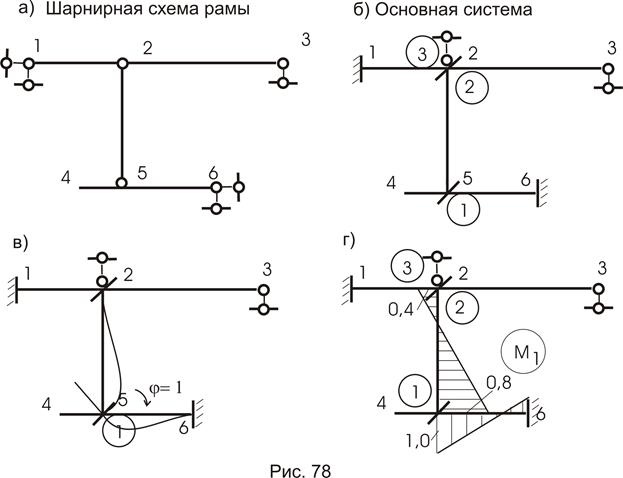
эпюры изгибающих моментов (рис. 78г), используя уже готовые решения (таблица 4). Вырезая узел со связью 1 (рис. 81), найдем . Направление считаем положительным, если оно направлено по направлению перемещения связи:

Перемещение связи 1 вызывает реакции во введенных связях 2 и 3. Вырезаем узел со второй связью (рис. 79б) и найдем :

Для получения величины в третьей связи проводим сквозное сечение. Оно пройдет по связи 3, по опоре 1, 6, далее по опоре 3 (рис.80). Реакции в опорах 1, 3 равны нулю, а реакция в опоре 6 равна (по табличным данным). Знак или направление будет зависеть от направления перемещения третьей связи. Не будем торопиться с этим.

Дадим перемещение второй связи – угол поворота узла 2 по часовой стрелке (рис. 81), т. е. перейдем к определению величины и производных от этого перемещения. Деформируются стержни, сходящиеся в узел 2 (рис.81). По табличным решениям строим эпюру М 2 (рис. 82а).

Вырезая узел со связью 2, из его равновесия найдем (рис.82б).

Вырезая узел 5 со связью 1, определим , но , а мы уже определили .

Читатель может еще раз проверить наши рассуждения. Мы не будем

торопиться с определением .

Даем перемещение третьей связи на единицу (рис. 83). Теперь самое время вернуться к определению (рис. 80). Возьмем перемещение третьей связи вверх (как направили на рис.80, но это совсем необязательно).Для деформированных стержней (рис.83) строим эпюры М , используя таблицу (рис. 81). Теперь проецируя на ось у усилия 0,375 и из рисунка 80, находим:

Проверим. Вырежем из М 3 узел 5 с первой связью (рис. 85а):

Видим полное совпадение

Вырезая узел 2 со второй связью, найдем и (рис. 85б):

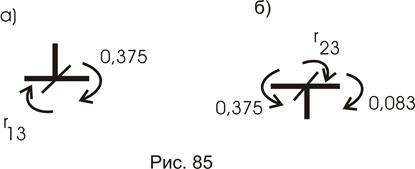
Для определения проведем сечение по связи третьей и по опорам 1, 6, 3, получим (рис. 86).

Рассмотрим раму, нагруженную силами, приложенными в узлах.

Пренебрегая изменением длин стержней и их весом, можно считать, что при достаточно малых значениях сил все стержни остаются прямыми и в них возникают только продольные усилия. При достижении нагрузкой критического значения наряду с исходным появляется смежное, деформированное состояние равновесия.

Такой подход является идеализированным (как и при расчете центрально сжатых стержней), т.к реальные нагрузки имеют эксцентриситет приложения, а также имеется начальный прогиб элементов от их собственной массы.

Для расчета рам на устойчивость можно использовать те же методы, что и для расчета на прочность: метод сил, метод перемещений, смешанный метод и т.др.

Смысл расчета рам на устойчивость заключается в определении для всех сжатых элементов критических сил Р кр и их расчетных длин

Расчету на устойчивость предшествует расчет рамы на прочность любым из известных методов. Затем рама рассчитывается на устойчивость под действием только узловых сжимающих нагрузок, которые берут из эпюры Nрасчета на прочность.

Порядок расчета рам на устойчивость методом перемещений

Порядок расчета рам на устойчивость аналогичен расчету на прочность.

1. Определяют степень кинематической неопределимости рамы

где степень угловой подвижности рамы, равна числу жестких узлов;степень линейной подвижности, равна числу возможных независимых перемещений узлов рамы.

2. Выбирают основную систему метода перемещения, для чего в каждый жесткий узел вводят упругоподатливые защемления (связи 1 го рода), а по направлению возможных перемещений - дополнительные опорные стерженьки (связи 2 го рода).

Например:

Заданная система Основная система

3. Составляют систему канонических уравнений. В отличие от аналогичных уравнений расчета на прочность (поперечный изгиб) грузовые коэффициенты R ip равны нулю, т.к. узловые нагрузки не вызывают реактивных усилий в дополнительных связях. Система канонических уравнений записывается:

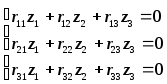
Действие внешней нагрузки в данном случае учитывается при вычислении единичных коэффициентов r ik =r ki , т.к. при единичных смещениях дополнительных связей деформируемые элементы, в пределах которых действуют сжимающие усилия, находятся в условиях продольно-поперечного изгиба.

4. Порядок определения опорных реакций с учетом сжимающих сил покажем на примере балки, у которой один конец жестко защемлен, другой шарнирно оперт.

M A  A =1 N

R A R B Для того, чтобы основная система и

заданная были равноценны необходимо чтобы М А имел такую величину, при которой А =1.

,

.

Обозначим:

, где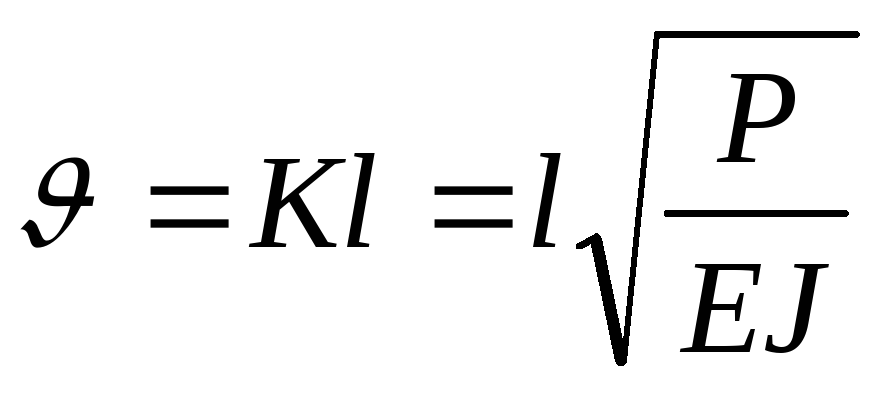

т.е.

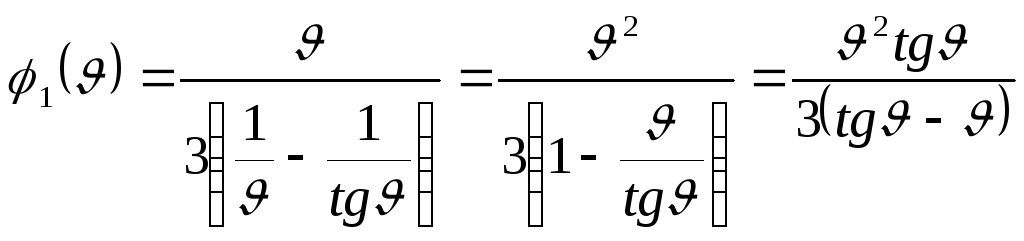
Аналогично получают реакции опор и в других случаях.

Схемы и эпюры	Коэффициенты
P P

5. Строят эпюры от единичных смещений наложенных связей. В пределах элементов, которые сжаты внешней нагрузкой, эпюры криволинейны и строятся в соответствии с приведенной выше таблицей. В пределах элементов не подверженных сжатию, эпюры прямолинейны и строятся по таблицам обычного метода перемещений (как при расчете на прочность) .

P 1 P 2 P 1 P 2

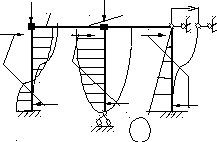
6. Коэффициенты системы канонических уравнений определяют как и в обычном методе перемещений.

7. Для заданной системы уравнений (без свободных членов), возможны два решения: первое, когда все z i = 0, такое решение нас не устраивает, т.е не соответствует условиям задачи; и второе решение, когда детерминант системы, составленный из единичных коэффициентов = 0.

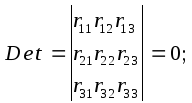
Раскрывая этот определитель, получаем сложное трансцендентное уравнение, для решения которого необходимо вначале выразить все параметры v i через один. Затем уравнение решается:

1) методом подстановки;

2) графическим методом.

Метод подстановки самый примитивный способ решения. Применяется для простейших характеристических уравнений.

Сущность графического способа заключается в следующем:

Выбираем произвольное значение параметра v i и находимdet 1 =f(v)

На основании полученных значений строим график функции det=f(v).

v 1 v 2 v 3 v 4 v 5 v

Наименьшее значение параметраv, при которомdet= 0 называетсяv кр.

8. Для стойки, параметры которой мы принимаем за исходные определяем критическую силу:

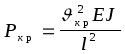
и расчетную длину стержня:

, отсюда

где:l 0 - расчетная длина стержня;

l - геометрическая длина стержня

или коэффициент приведения геометрической длины к расчетной:

9. Зная соотношение между параметрами остальных элементов и исходным элементом, определяют v кр для всех остальных сжатых стержней.

10. Затем для всех сжатых стержней определяют Р кр иl 0. .

Рассмотрим построение эпюр изгибающих моментов, поперечных и продольных сил для рамы, изображенной на рис. 7.41, от заданной нагрузки. Длины элементов рамы, соотношения моментов инерции и схема нагрузки даны на том же рисунке.

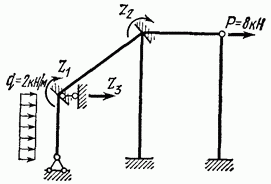
При расчете рамы целесообразно использовать метод перемещений, так как степень ее статической неопределимости (а следовательно, и число неизвестных при расчете рамы методом сил) равна 4, число же неизвестных (степень кинематической неопределимости) при расчете рамы методом перемещений равно 3, т. е. меньше, чем при расчете методом сил. Расчет проводим в указанной последовательности.

1. Выбор основной системы. Поставим (рис. 7.42) две плавающие заделки в узлах рамы и горизонтальный стержень, препятствующий горизонтальным перемещениям узлов. Неизвестные перемещения обозначим . В результате получим основную систему, состоящую из двух балок, защемленных по концам, и трех балок, защемленных одним концом и с шарнирным опиранием другого конца.

2. Построение эпюр изгибающих моментов для основной системы.

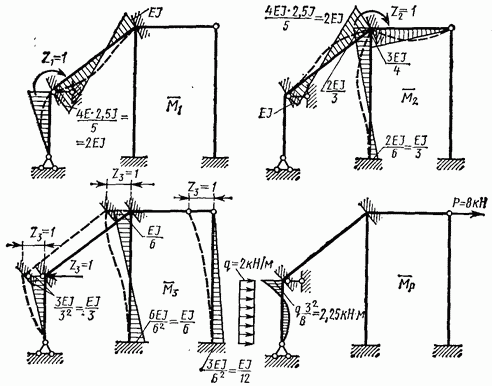
Для вычисления коэффициентов при неизвестных и свободных членов канонических уравнений построим для основной системы единичные и грузовую эпюры изгибающих моментов (рис. 7.43).

3. Определение коэффициентов и свободных членов системы канонических уравнений приведено в табл. 7.3.

4. Проверка коэффициентов и свободных членов системы канонических уравнений. Для контроля коэффициентов уравнений и свободных членов построим эпюру (рис. 7.44, а) суммированием четырех единичных эпюр, приведенных на рис. 7.43. Умножив

эпюру на ту же эпюру получим

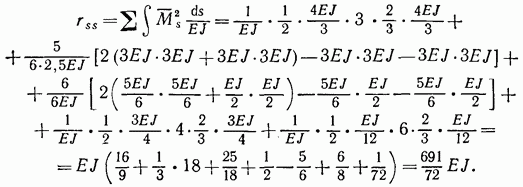
Теперь подсчитаем сумму всех единичных коэффициентов (табл. 7.3):

Сравнивая полученное значение коэффициентов с результатом перемножения эпюр, убеждаемся в том, что они равны, т. е. условие (7.11) удовлетворяется и, следовательно, коэффициенты вычислены правильно.

Произведем проверку свободных (грузовых) членов. Для этого построим эпюру от внешней нагрузки в статически определимой системе, полученной из заданной удалением лишних связей. Эта эпюра изображена на рис. 7.44, б. Для определения суммы всех грузовых коэффициентов умножим эпюру на

Сумма грузовых коэффициентов (см. табл. 7.3) будет

Сравнивая эти два результата, убеждаемся в том, что условие (7.13) удовлетворяется и свободные члены найдены правильно.

5. Решение системы уравнений. Канонические уравнения, отрицающие реакции во введенных связях основной системы, имеют вид

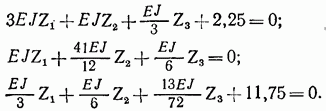
Таблица 7.3. (см. скан)

Таблица 7.4

Проверим правильность решения системы уравнений:

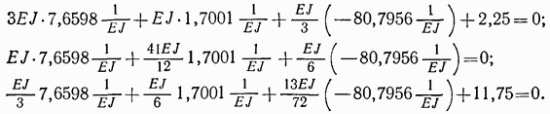
С точностью до двух знаков после запятой получились тождества, следовательно, значения неизвестных определены правильно.