Напряжение по наклонным площадкам при плоском напряженном состоянии. Напряжения в наклонной площадке
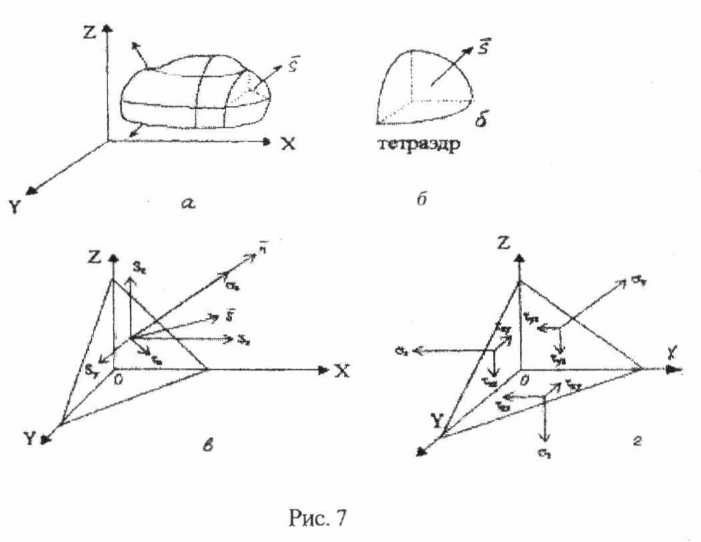
При решении задач обработки металлов давлением часто требуется знать связь между внешними силами на поверхности твердого деформируемого тела и напряжениями, действующими внутри, а также между напряжениями на плоской площадке внутри тела и напряжениями на трех взаимно перпендикулярных площадках. Для установления этой связи рассмотрим тело под действием внешних сил в состоянии равновесия. Рассечем его множеством взаимно перпендикулярных сечений, параллельных координатным плоскостям, (рис. 7, а).
Выделенный бесконечно малый элемент на поверхности тела представляет собой тетраэдр (рис. 7,6). Криволинейную поверхность тетраэдра заменим наклонной площадкой (рис. 7в), положение которой в пространстве определяется направляющими конусами:
cos(n , х)= n х ,
cos (п, у)= n у ,
cos(п, z)=n z ,
где - внешняя нормаль к наклонной площадке.
Обозначим площадь наклонной площадки ∆ F . Тогда площади
других граней тетраэдра представляют собой проекции площадки ∆ F на координатные плоскости:
Пусть на наклонную площадку действует вектор внешних сил . Его проекции на координатные оси: Sx, Sy, Sz. Известны также напряжения на трех взаимно перпендикулярных площадках, параллельных координатным плоскостям, внутри тела. Выделенный тетраэдр находится в равновесии. Из условия равновесия следует, что суммы всех действующих по его граням сил на оси координат равны 0. Перейдем от напряжений к силам, умножая каждое напряжение на площадь соответствующей грани. Получим:
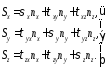 (2)
(2)
Эти уравнения впервые получены Коши. Они связывают проекции на оси координат полного напряжения с напряжениями, действующими на трех взаимно перпендикулярных площадках. Суммируя компоненты Sx, S y , Sz по правилу параллелепипеда, получим полное напряжение S:
Нормальное напряжение на наклонной площадке ап определяется как сумма проекций Sx, Sy, Sz на нормаль к площадке:
Полное касательное напряжение т на наклонной площадке находится по правилу параллелограмма:
По полученным формулам можно найти напряжения на любой тонной площадке, проходящей через заданную точку внутри формируемого тела, если известны в этой точке напряжения по трем взаимно перпендикулярным площадкам, параллельным координатным плоскостям.
Задача 6. Напряженное состояние в исследуемой точке тела задано тензором напряжений
Размерность компонент тензора приведена в МПа. Для площадки, нормаль к которой определяется направляющими косинусами = 2/3 ,= 2/3 , найти полноеS , нормальное и касательноеτ напряжения.
Полное напряжение
Нормальное напряжение
Касательное напряжение
![]()
1.6. Главные нормальные напряжения
Среди трех взаимно перпендикулярных площадок, проходящих через любую точку нагруженного тела, найдутся такие, на которых касательные напряжения отсутствуют. Такие площадки называются главными, а соответствующие им нормальные напряжения - главными нормальными напряжениями. Существование главных площадок доказывается следующим образом.
Рассмотрим выражение для расчета σ n на наклонной площадке:
После подстановки в него (2) получим (3)
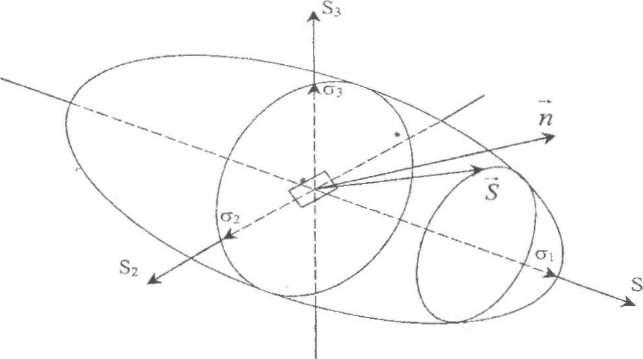
Отложим от начала координат к наклонной площадке, проходящей через заданную точку А, радиус-вектор по направлению нормали (рис. 8.)
Величину радиуса-вектора возьмем обратно пропорциональной величине нормального напряжения:
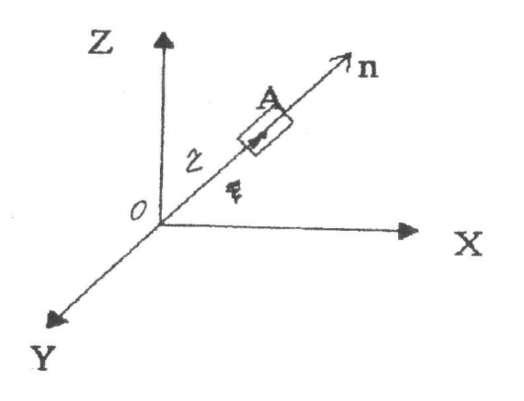
где с – произвольная постоянная, определяющая масштаб.
Координаты вектора :
Отсюда значения направляющих косинусов:
Представляя эти значения в уравнение (3), порлучим алгебраическое уравнение второй степени:
Полученное уравнение представляет собой поверхность второго порядка, отнесенную к центру координат - эллипсоид . В уравнении отсутствуют члены с х,у,z, определяющие смещение эллипсоида относительно начала координат. Концы радиус-вектора будут лежать на этой поверхности. Найденная поверхность называетсяповерхностью напряжений (эллипсоидом напряжений).
Изменяя направление осей координат, можно преобразовать равнение поверхности таким образом, что в нем обратятся в нули коэффициенты при членах, содержащих парные произведения координат, т.е.
Оси координат, при которых члены, содержащие произведение координат, обращаются в нуль, называются главными осями, а нормальные напряжения, направленные по этим осям, - главными нормальными напряжениями. Следовательно, когда за координатную систему взята система главных осей, то на координатных плоскостях, являющихся главными площадками, не будет касательных напряжений.
По напряжениям в данной точке можно отыскать главные напряжения и их направления. Допустим, что для данной точки наклонная площадка является главной. Тогда и полное напряжениеS этой площадке будет направлено по нормали (рис.9).
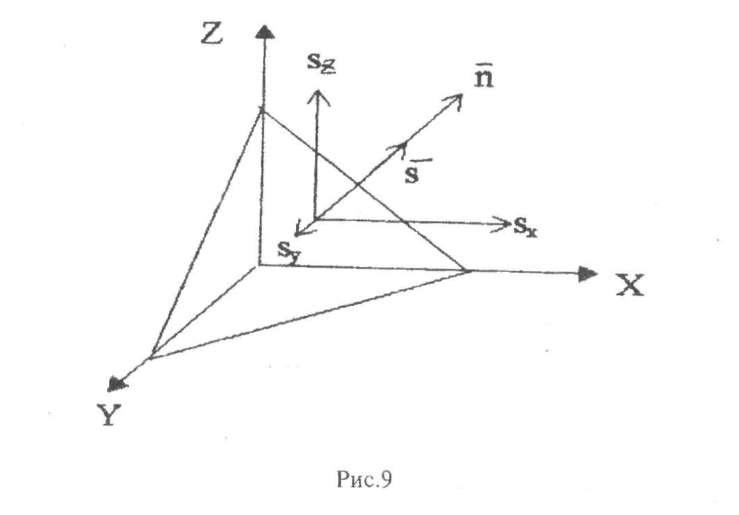
Обозначив искомое главное нормальное напряжение, действующее на наклонной площадке, положение которой определяется п х , n у , n z , через σ и проектируя его на координатные оси, находим составляющие главного напряжения, параллельные координатным осям:
Приравнивая полученные соотношения условиям Коши, получим:
Полученная система может быть решена как система из трех линейных однородных уравнений с тремя неизвестными п х , п у , n z . С учетом тензорных обозначений запись будет выглядеть Полученная система не допускает тривиального решения, так как сумма квадратов направляющих косинусов.
Следовательно, система (4) будет иметь решение, отличное от нуля при условии, что определитель, составленный из коэффициентов при неизвестных, равен нулю:
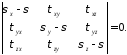
Раскрываем определитель:
Первое слагаемое этого уравнения равно
После его подстановки и преобразований получаем уравнение третьей степени относительно σ:
Или где- коэффициенты кубического уравнения, не изменяющие своих значений при изменении положения координатных осей. Их называют инвариантами тензора напряжений. Линейный инвариант
Квадратичный вариант
Кубический инвариант
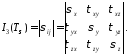
Решая кубическое уравнение, получаем три главных напряжения σ 1 , σ 2, σ 3 ,которые располагаются следующим образом: . Каждому главному напряжению будет соответствовать главная ось, для которой направляющие косинусы находятся из решения системы уравнений. Для 1-го главного напряжения уравнение имеет вид
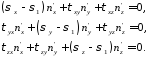
Сюда же добавляется условие
![]()
Вообще, достаточно найти положение одной главной площадки, так как две другие взаимно перпендикулярны. Тензор напряжений в главных осях имеет вид
Если в обычных осях напряженное состояние в точке задается шестью числами: σ x , σ y , σ z , σ xz , σ yz , σ xy , то в главных осях тремя значениями главных напряжений и тремя направляющими косинусами, определяющими положение одной из главных площадок. Если напряженное состояние задано главными напряжениями, то выражения напряжений, действующих на наклонной площадке, значительно упрощаются.
Составляющие полного напряжения в каждой точке тела:
где n 1 , n 2 , n 3 - направляющие косинусы главных площадок 1, 2 и 3 соответственно.
Полное напряжение
Нормальное напряжение
Касательное напряжение
Значения инвариантов тензора напряжений в системе главных осей:
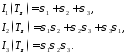
Из уравнения (5) следует, что
Учитывая, что
получаем уравнение эллипсоида напряжений, отнесенное к центру и главным осям (рис.10):
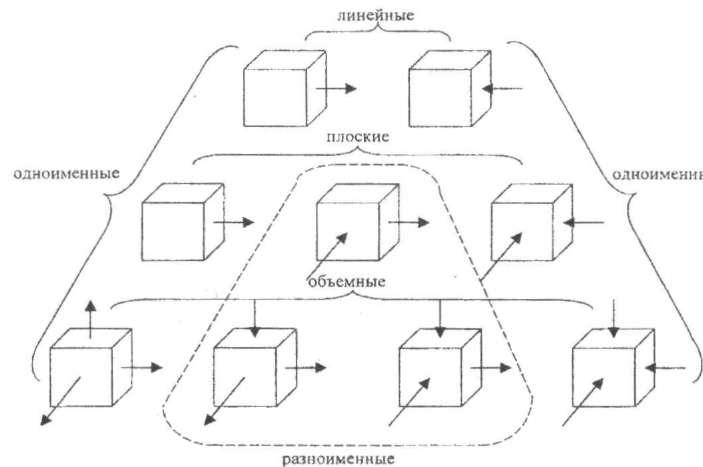
Исходя из количества действующих напряжений на трех взаимно перпендикулярных площадках, возможны девять схем главных нормальных напряжений: линейные, плоские и объемные (рис. 11). Схемы представлены графически в виде кубиков, грани которых ориентированы в направлении действия главных напряжений. Наличие напряжения и его направление обозначаются стрелкой.
Если одно из главных нормальных напряжений равно нулю, то эллипсоид (6) превращается в эллипс и объемное напряженное состояние преобразуется в плоское. Если два главных нормальных напряжения равны нулю, то эллипсоид (6) превращается в отрезок прямой линии, что соответствует линейному напряженному состоянию. Схемы, имеющие напряжения одного знака, называют одноименными , а разных знаков - разноименными. Схемы дают графическое представление о наличии и знаке главных нормальных напряжений. Они являются по предложению С.И. Губкина классификатором всех видов напряженного состояния деформируемого тела.
От схем главных нормальных напряжений зависит пластичность деформируемого тела и его сопротивление деформированию (усилие деформирования).Пластичность металла всегда больше в схемах со сжимающими напряжениями, чем в схемах с растягивающими напряжениями. Наибольшим сопротивлением деформированию отличаются металлы в условиях деформирования при одноименных схемах. В условиях разноименных схем, а также линейной, сопротивление деформации снижается (рис. 12).
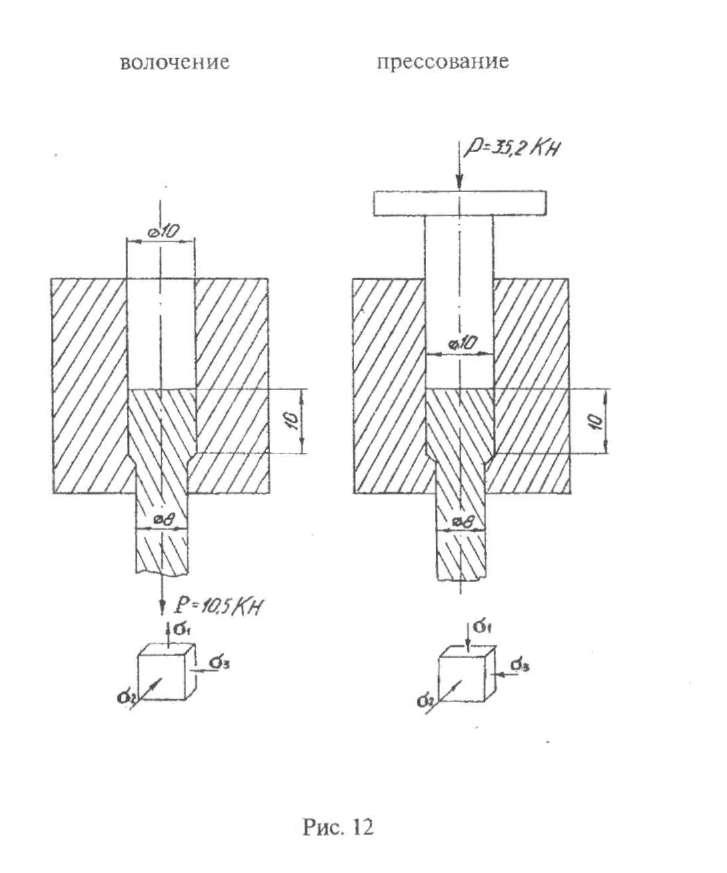
Схемы линейного напряженного состояния встречаются па практике редко. Схема линейного растяжения реализуется, например, при растяжении тела, длина которого значительно больше размеров в остальных двух измерениях (растяжение струны, канатов и т.п.). Плоская схема напряженного состояния с известным приближением может быть создана при растяжении тонкой пластины по контуру. Объемное напряженное состояние возникает почти при всех процессах обработки металлов давлением (прокатка, прессование, горячая штамповка, волочение).
Определить главные нормальные напряжения и направления главных осей.
Решение. Для нахождения главных нормальных напряжений составим определитель:
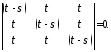
Раскроем его по первой строке, т. е. возьмем в виде произведения элементов первой строки на алгебраическое дополнение:
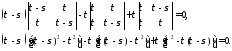
Получим кубическое уравнение
![]()
или отсюда получим корни этого уравнения.
Напряжения на площадках наклонных к оси.
Рассмотрим
стержень равномерно растянутый силой F. Определим напряжение на
площадке, расположенной под углом A(альфа) к поперечному сечению
(рис. 4.3). Угол (альфа) условимся считать положи-тельным, когда
поперечное сечение для совмещения с наклонным сечением надо повернуть на
угол (альфа) против часовой стрелки.
Удлинение всех волокон,
параллельных оси бруса, при его растяжение одинаковы (однородное
напряженное состояние), следовательно напряжения Р во всех точках
наклонного сечения одинаковы.
Рассмотрим левую отсеченную часть
бруса: из условия равновесия внутренняя сила равна р A(альфа) . Где р-
полное напряжение на площадке.
Внешняя сила равна, так же F=σA, где σ- нормальное напряжение в поперечном сечении бруса.
Поперечное сечение бруса связано с наклонным соотношением
Определим полное напряжение на площадке:
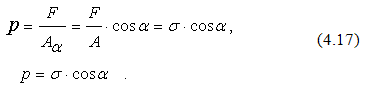
Разложим полное напряжение р на составляющие по осям: нормальное σа- перпендикулярное наклонной площадке и касательное тσ- перпендикулярно ей (рис 4.4)
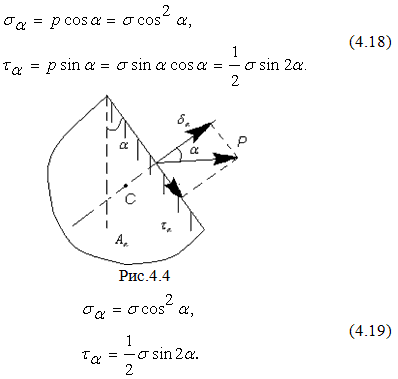
Нормальное напряжение считается положительным при растяжении и отрицательным при сжатии. Касательное напряжение положительно, если изображающий его вектор стремится вращать тело относительно любой точки С, лежащей на внутренней нормали к сечению по часовой стрелке (рис.4.4).
Из формулы (4.19) следует, что
1) при . Максимальное нормальное напряжение возникает в поперечном сечении бруса, ![]() .
.
2) при . Максимальное касательное напряжение возникает в сечении, наклонном под углом 45 к поперечному сечению.
3) при . В продольных сечениях бруса ![]() .
.
Таким образом, расчет прочности при растяжении или сжатии бруса производят по нормальным направлениям в поперечных сечениях, т.к. σmаx, при альфа=0 .
В более сложных случаях нагружения бруса, вопрос об определении наибольших напряжений, а так же положения площадок, на которые они действуют, усложняется. Для решения этого вопроса приходится исследовать законы изменения напряжений при изменении наклона площадок, проходящих через одну точку.
Контрольные вопросы:
1. Как распределяются нормальные напряжения в поперечном сечении при осевом растяжении (сжатии)? Чему они равны?
2. Чем отличается расчет на прочность конструкций из пластичных и хрупких материалов?
3. Какие три характерных вида задач встречаются при расчете на прочность?
4. Что такое абсолютная продольная деформация? Абсолютная поперечная деформация?
5. Что такое относительная продольная деформация? Относи-тельная поперечная деформация?
6. Что называется коэффициентом поперечной деформации (коэффициентом Пуассона)?
7. Что называется модулем упругости I рода?
8. Какие формулы, выражающие закон Гука, Вы знаете?
9. Как определить перемещение произвольного сечения?
10. Как формулируется условие прочности?
11. Как определяются напряжения на площадках наклонных к поперечному сечению?
При расчете инженерных конструкций нет необходимости определять напряжения во всех площадках, проходящих через данную точку; достаточно знать экстремальные (т. е. максимальные и минимальные) их значения.
Максимальные и минимальные нормальные напряжения называются главными напряжениями, а площадки, по которым они действуют, - главными площадками.
Для определения величины главных напряжений и положений главных площадок приравниваем нулю первую производную напряжения по углу а [см. формулу (6.3)]:
Здесь - углы наклона главных площадок к площадке, в которой действует напряжение ад. (см. рис. 2.3). Сравнивая последнее выражение с формулой (7.3), устанавливаем, что
![]()
Следовательно, по главным площадкам касательные напряжения равны нулю.
Поэтому главными площадками можно называть площадки, по которым касательные напряжения равны нулю.
Решим уравнение (9.3) относительно угла
![]()
или на основании (5.3)
![]()
Формула (10.3) или (11.3) дает значения углов определяющие две взаимно перпендикулярные площадки. Следовательно, обе главные площадки взаимно перпендикулярны. Для определения их положений площадки, в которых действуют напряжения следует повернуть на угол против часовой стрелки (при или по часовой стрелке (при
При любом значении полученном по формуле (10.3) или (11.3), можно установить соответствующую величину угла находящуюся в интервале от -90 до +90°, и, следовательно, значение от -45 до +45° Поэтому поворот площадок всегда можно произвести на угол, не больший .
По одной из главных площадок действует максимальное напряжение. При решении конкретной числовой задачи для определения величин значения углов можно подставить в формулу (6.3). Решим эту же задачу в общем виде.
По формулам тригонометрии, используя выражение (10.3), найдем:
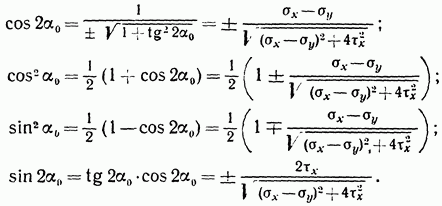
Подставив эти выражения в формулу (6.3), после простых преобразований получим выражения экстремальных нормальных напряжений
Для определения положения главной площадки с напряжением атах можно выполнить следующее: площадку с большим (в алгебраическом смысле) нормальным напряжением повернуть на угол (по абсолютной величине не больший 45°) в направлении, в котором вектор касательного напряжения, действующего по этой же площадке, стремится вращать элементарный параллелепипед относительно его центра.
После определения положения главной площадки с напряжением атах легко находится перпендикулярная к ней вторая главная площадка с напряжением .
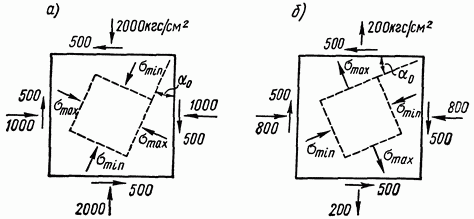
Такой прием позволяет приближенно определять положения главных площадок, не вычисляя значения а используя то обстоятельство, что угол всегда можно взять по абсолютной величине не большим 45°. Примеры такого приближенного определения даны на рис. 6.3, а, б.
или сжатии
При растяжении прямого бруса в поперечных сечениях возникают только нормальные напряжения, определяемые по формуле
Для определения
напряжений в наклонных сечениях при
растяжении в одном направлении проведём
наклонное сечение под углом
 (рис. 4.1).
(рис. 4.1).
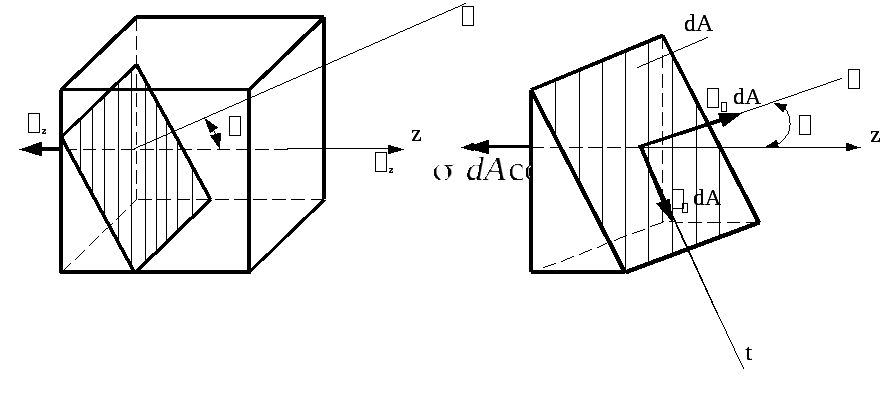 Рис.
4.1 Рис. 4.2
Рис.
4.1 Рис. 4.2
Составим уравнение равновесия элементарной трёхгранной призмы
(рис. 4.2). Площадь наклонной грани dA .
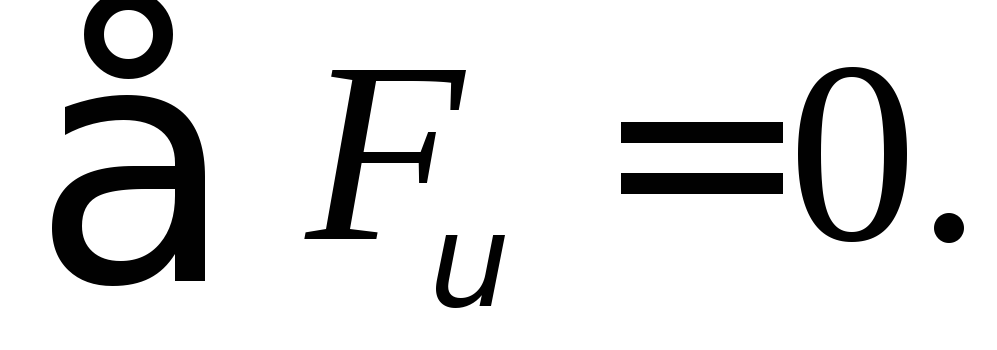 ,
(4.1)
,
(4.1)
откуда
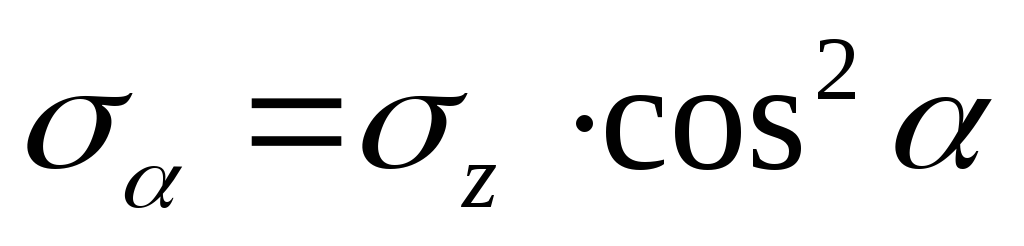 .
.
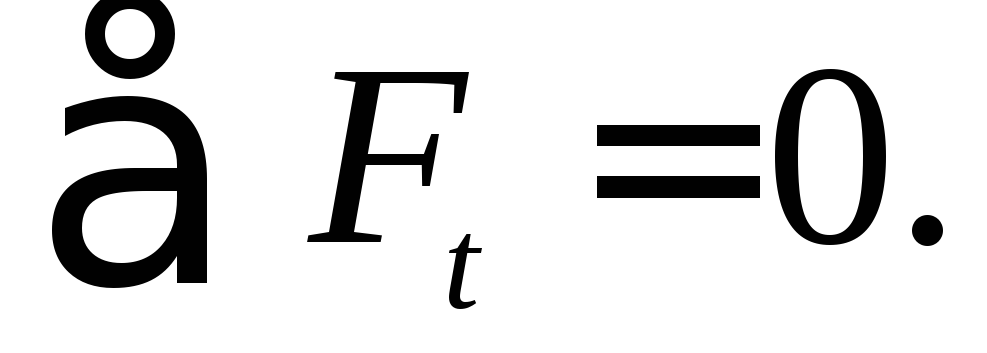 ,
(4.2)
,
(4.2)
откуда
 .
.
1) наибольшее нормальное напряжение возникает в поперечном сечении бруса:
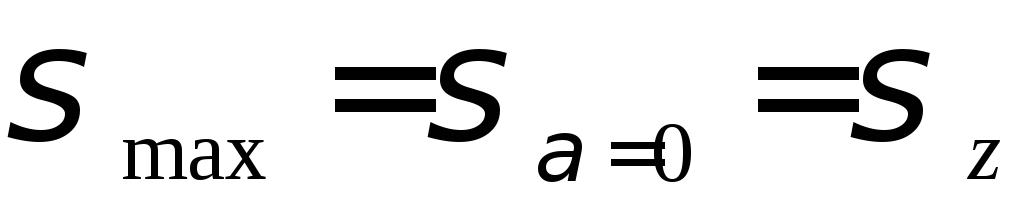 ;
;
2) наибольшее
касательное напряжение возникает на
площадке, наклонённой под углом
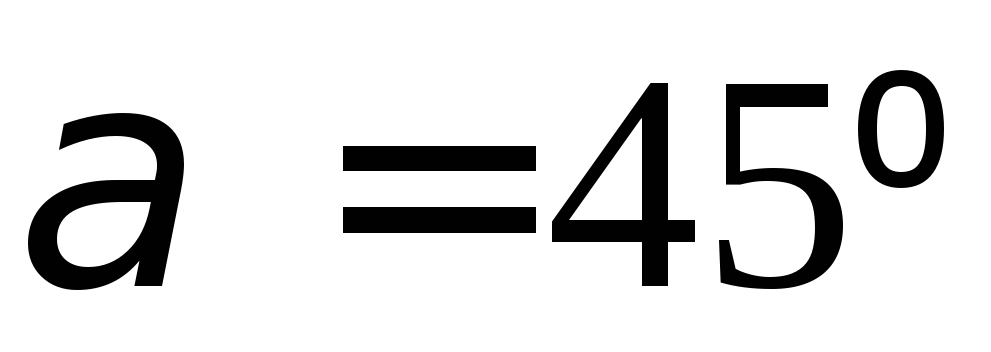 и
и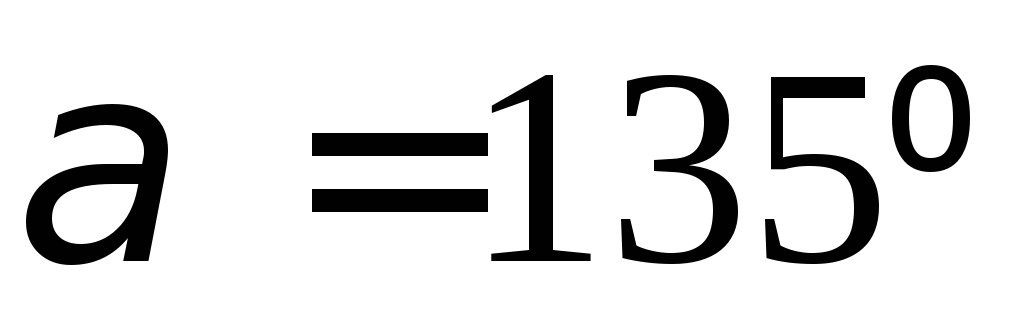 к оси бруса и равно половине нормального
напряжения, возникающего в соответствующей
точке поперечного сечения:
к оси бруса и равно половине нормального
напряжения, возникающего в соответствующей
точке поперечного сечения:
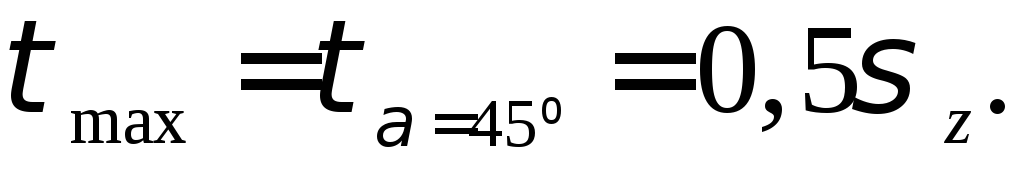
4.2. Напряжения на взаимно-перпендикулярных площадках
Определим нормальные и касательные напряжения на взаимно- перпендикулярных площадках (рис. 4.3).
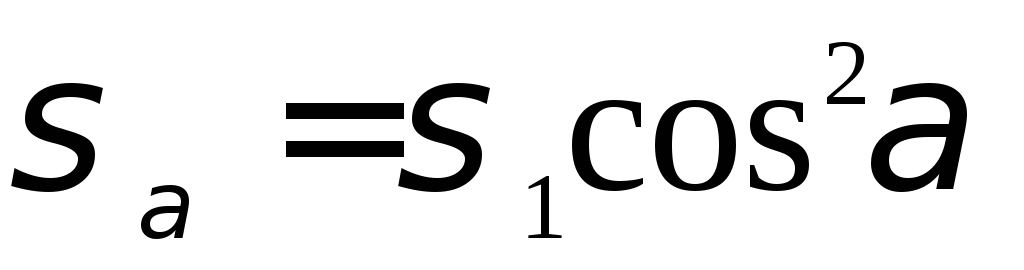 ;
;
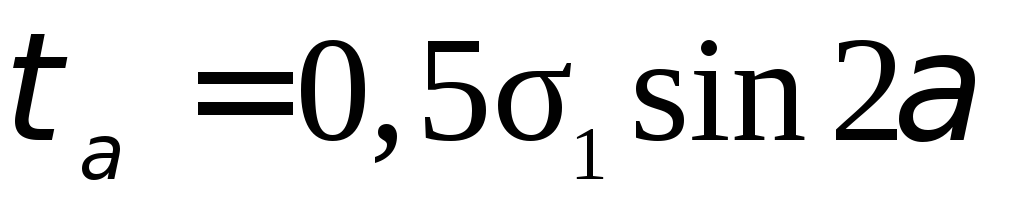 .
.
Для взаимно-перпендикулярной площадки:
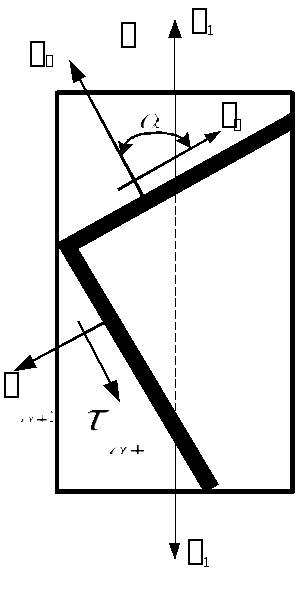
Анализируя полученные результаты, можно сделать вывод:
Сумма нормальных напряжений на двух взаимно – перпендикулярных площадках постоянна и равна главному напряжению.
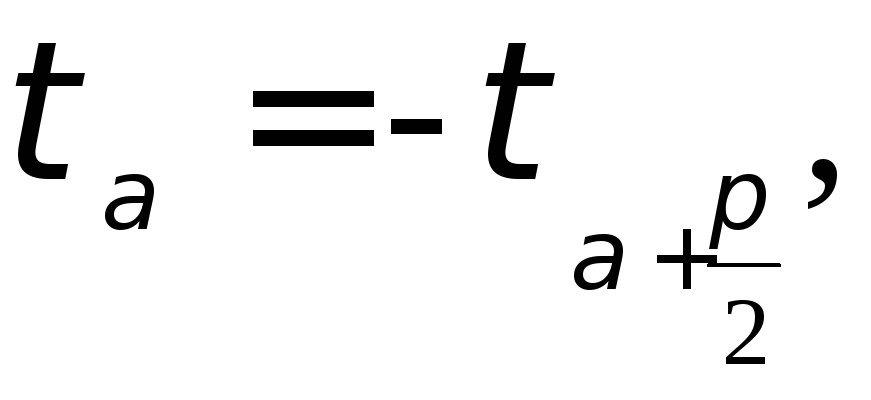 (4.4)
(4.4)
т.е. на двух взаимно-перпендикулярных площадках действуют равные по величине и обратные по знаку касательные напряжения (закон парности касательных напряжений).
4.3. Определение напряжений в наклонных сечениях при
растяжении или сжатии по двум взаимно-перпендикулярным
направлениям
При плоском
напряженном состоянии
![]()
М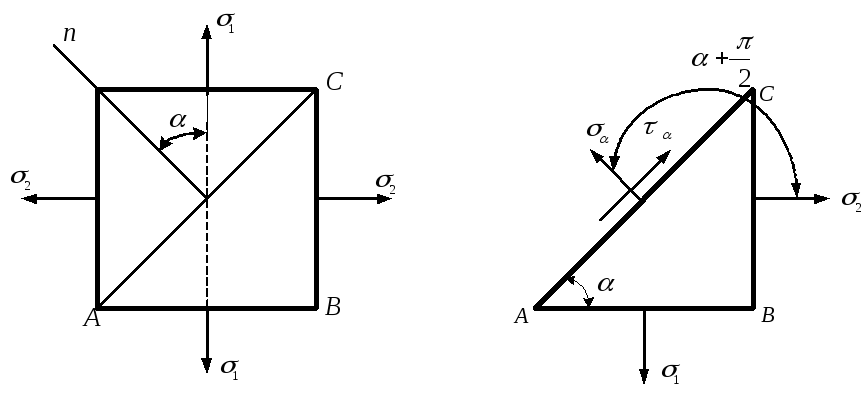 ежду
направлением
ежду
направлением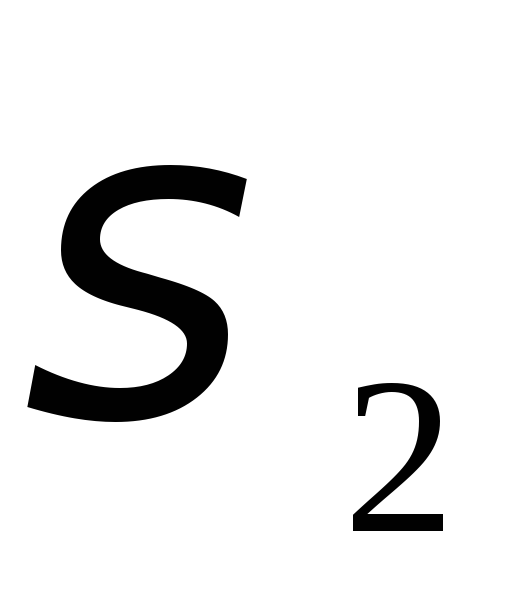 и площадкой угол равен
и площадкой угол равен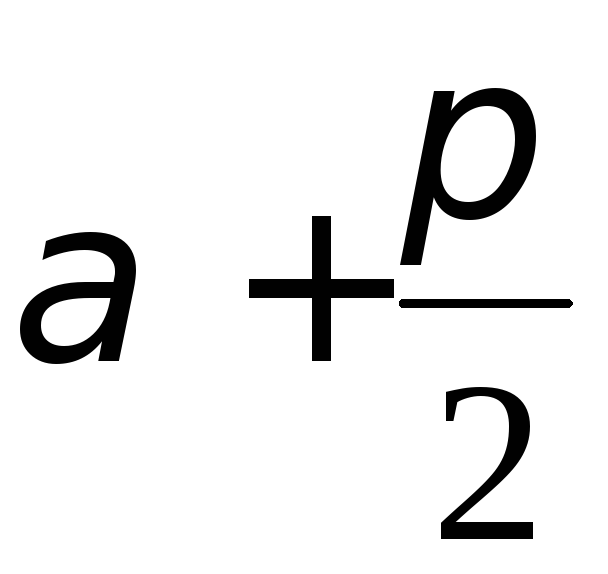 (рис. 4.4).
(рис. 4.4).
Рис. 4.4 Рис. 4.5
Напряжения
 и
и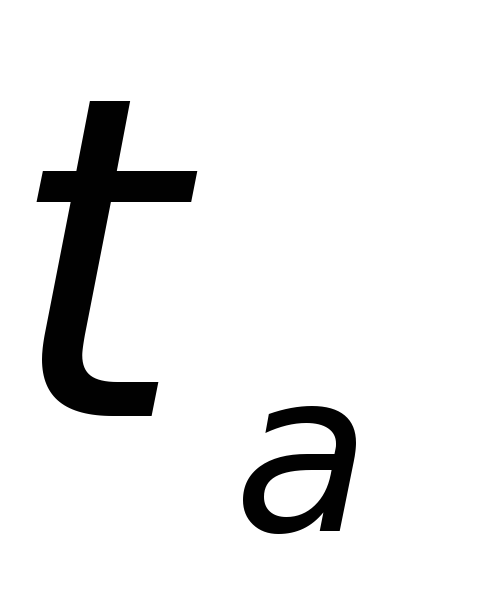 в произвольном наклонном сечении можно
определить из равновесия трёхгранной
призмыABC
(рис. 4.5) или по полученным формулам,
суммируя напряжения от действия
в произвольном наклонном сечении можно
определить из равновесия трёхгранной
призмыABC
(рис. 4.5) или по полученным формулам,
суммируя напряжения от действия
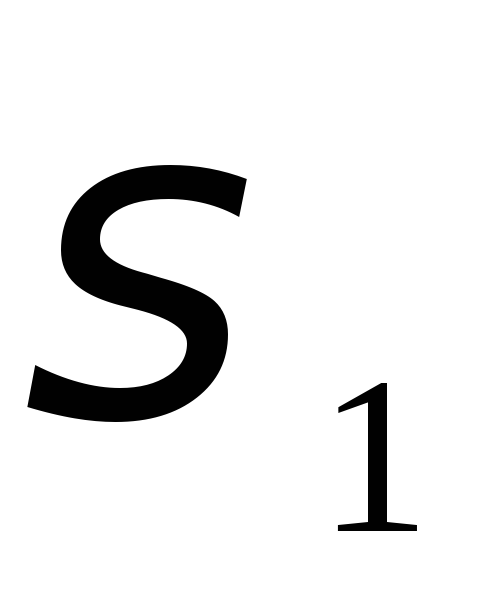 и
и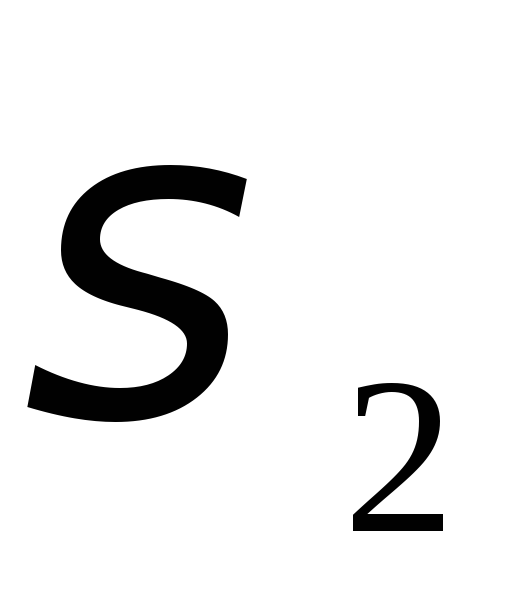 (при замене угла
(при замене угла на
на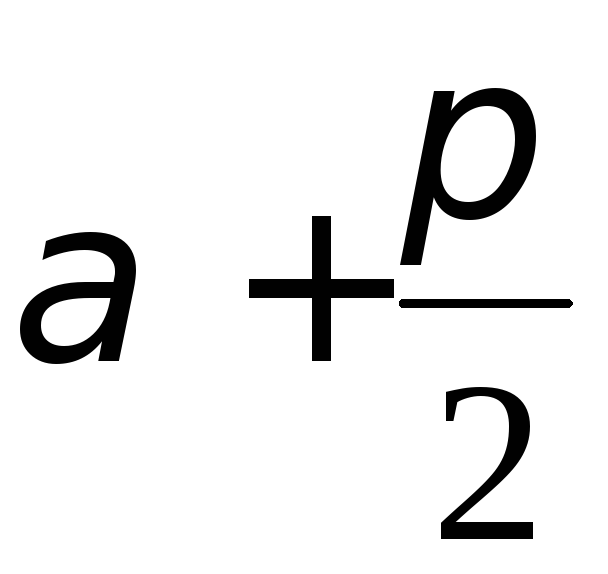 ).
).
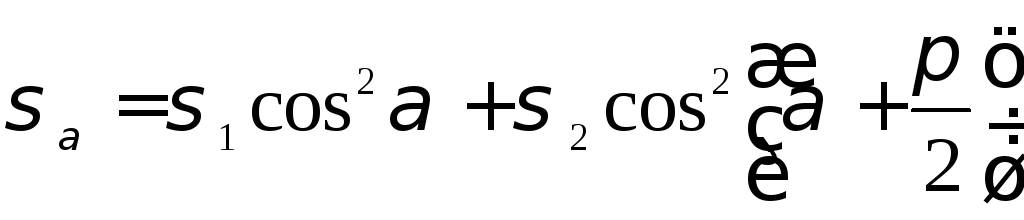 ,
,
откуда . (4.5)
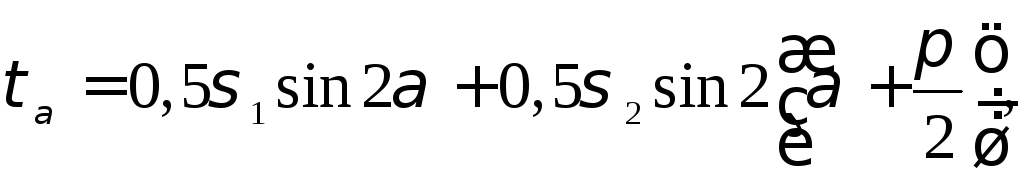
откуда . (4.6)
Из формулы (4.6) видно, что максимальные касательные напряжения равны полуразности главных напряжений
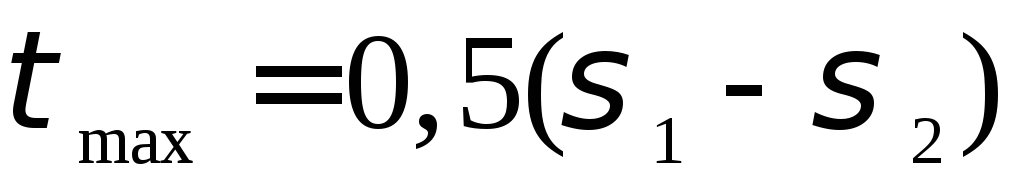
и действуют в
сечениях, одинаково наклоненных к
направлениям
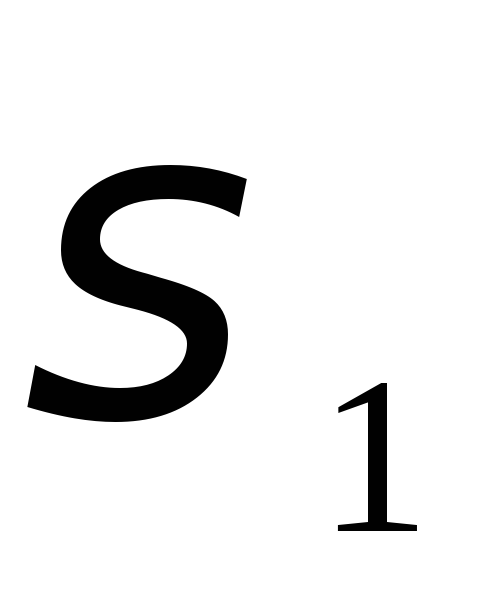 и
и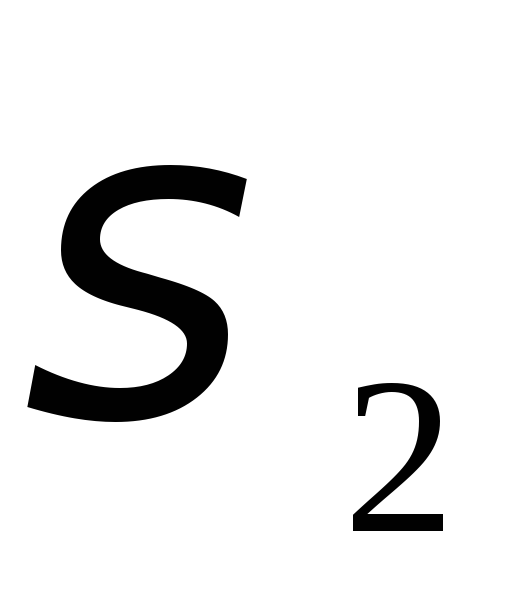 ,
т.е. при
,
т.е. при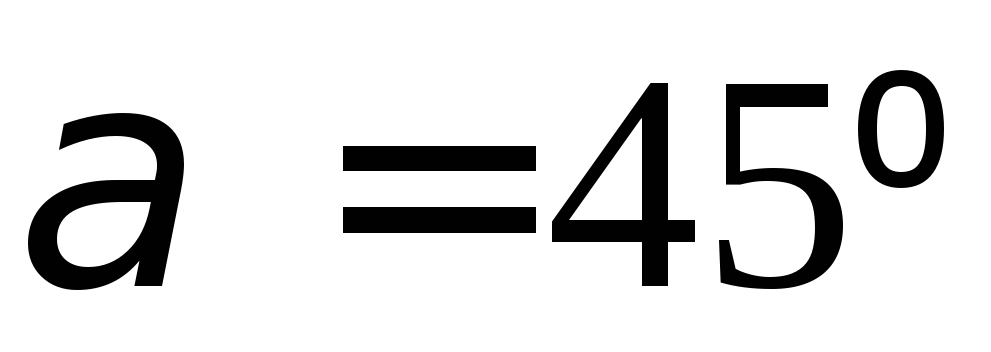 или
или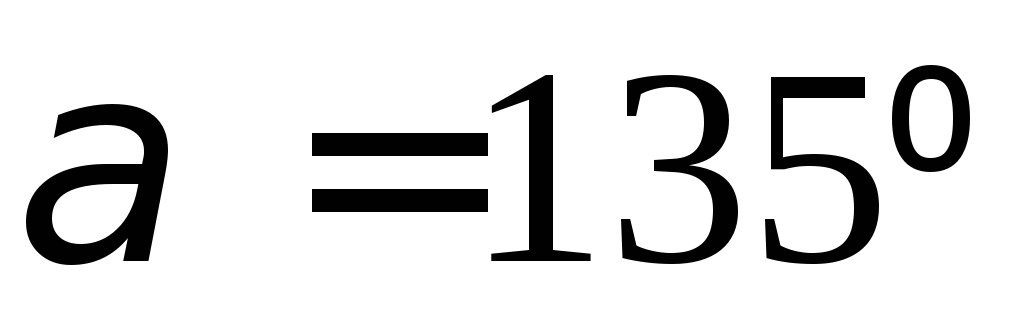 .
.
Для двухосного напряжённого состояния сохраняет свою силу закон парности касательных напряжений.
4.4. Определение главных напряжений и главных площадок
напряжения,
действующие по граням элемента (рис.
4.6). Требуется определить положение
главных площадок и значения главных
напряжений. Рассмотрим равновесие
трёхгранной призмы DB
С
(рис. 4.7).
Примем, что
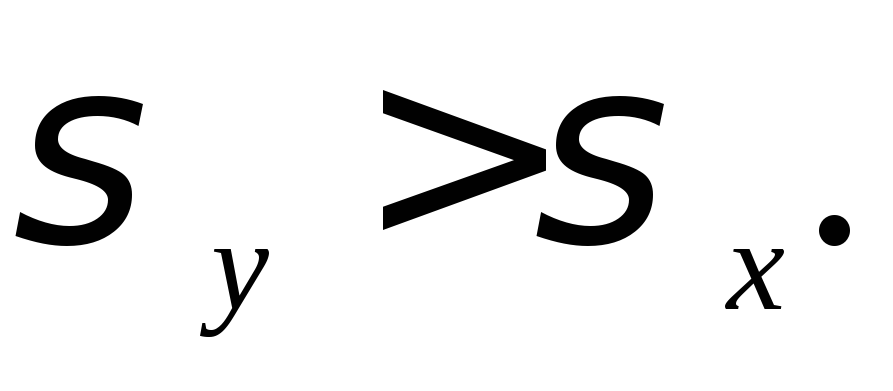 Угол
Угол будем отсчитывать от направления
большего напряжения до нормали к
площадке. За положительное направление
примем направление против хода часовой
стрелки. Площадь наклонной грани
обозначимdA
.
Тогда площадь вертикальной грани dA
будем отсчитывать от направления
большего напряжения до нормали к
площадке. За положительное направление
примем направление против хода часовой
стрелки. Площадь наклонной грани
обозначимdA
.
Тогда площадь вертикальной грани dA
 ,
а горизонтальной –dA
,
а горизонтальной –dA
![]() .
.
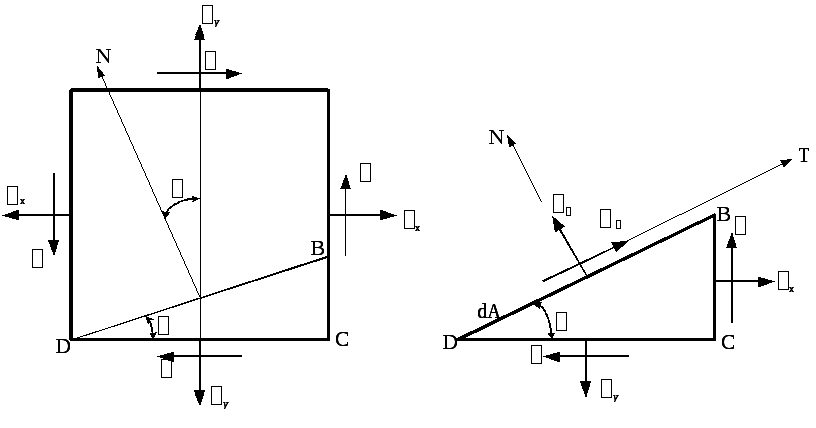
Рис. 4.6 Рис. 4.7
Проектируем все силы на ось N :
Проектируем все силы на ось Т :
Сократим на dA :
; (4.7) . (4.8)
Чтобы отыскать
положение главных площадок, нужно либо
приравнять нулю производную
 ,
либо приравнять нулю касательные
напряжения, т.к. на главных площадках
касательных напряжений нет.
,
либо приравнять нулю касательные
напряжения, т.к. на главных площадках
касательных напряжений нет.
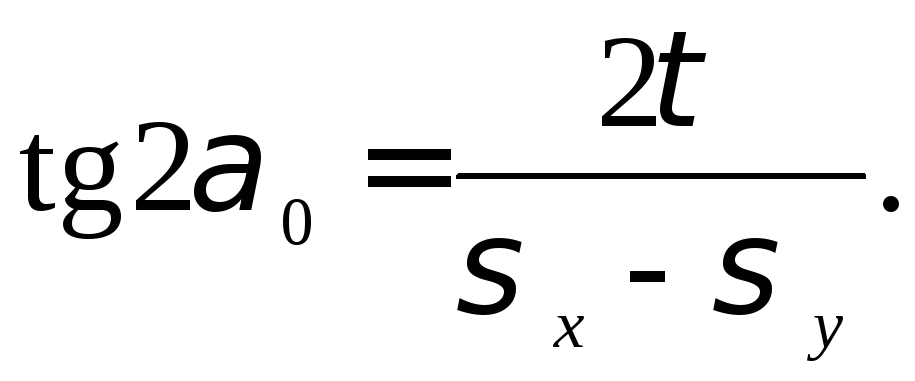 (4.9)
(4.9)
Для определения экстремальных значений напряжений, т.е. главных напряжений, значение угла из формулы (4.9) подставим в формулу (4.7). Предварительно тригонометрические функции в формуле (4.7) выразим через тангенс двойного угла, используя известные формулы тригонометрии:
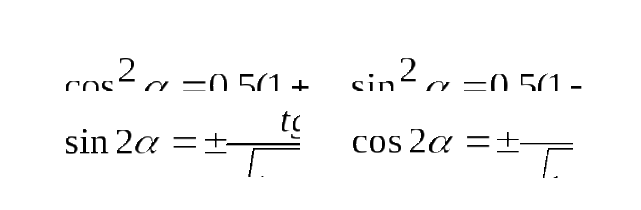
Далее вместо
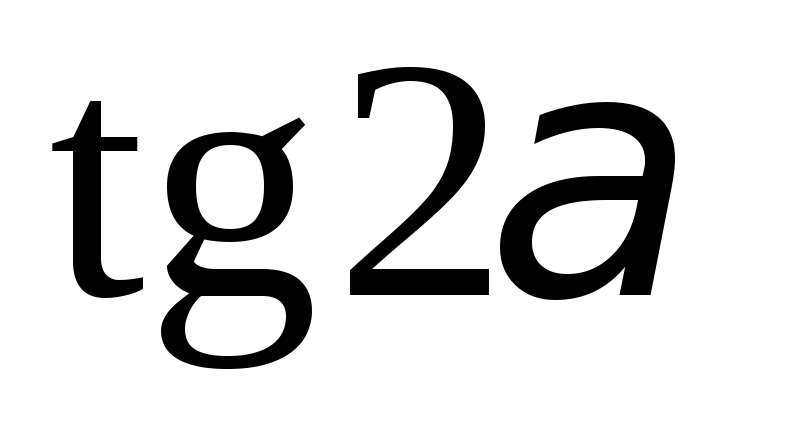 подставляем значение (4.9) и получаем
формулу для определения главных
напряжений:
подставляем значение (4.9) и получаем
формулу для определения главных
напряжений:
Если одно из заданных нормальных напряжений равно нулю, то формула (4.10) примет вид:
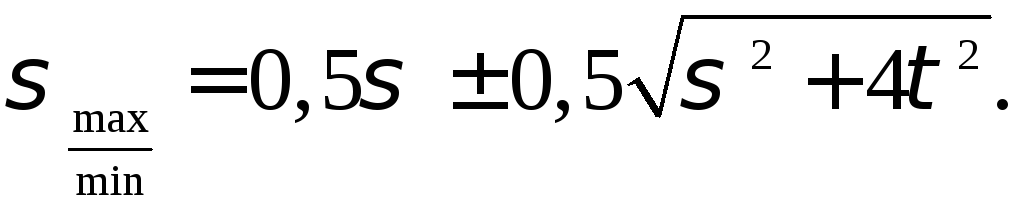 (4.11)
(4.11)
Этой формулой будем пользоваться при изучении сложного сопротивления.
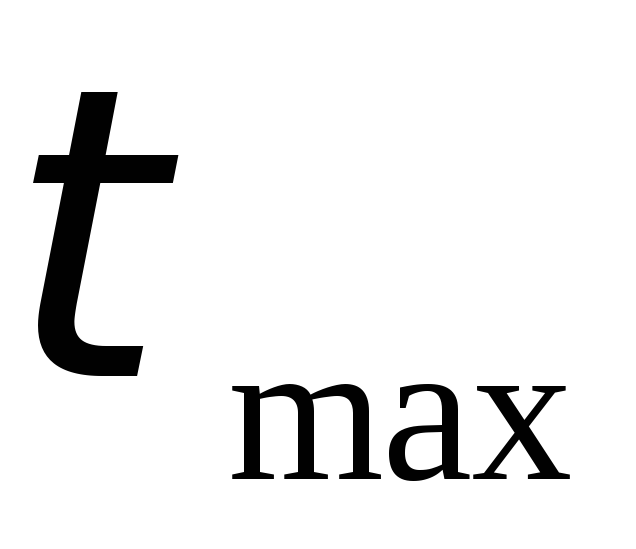 равны полуразности
главных напряжений, следовательно,
равны полуразности
главных напряжений, следовательно,
Если одно из нормальных напряжений равно 0, то
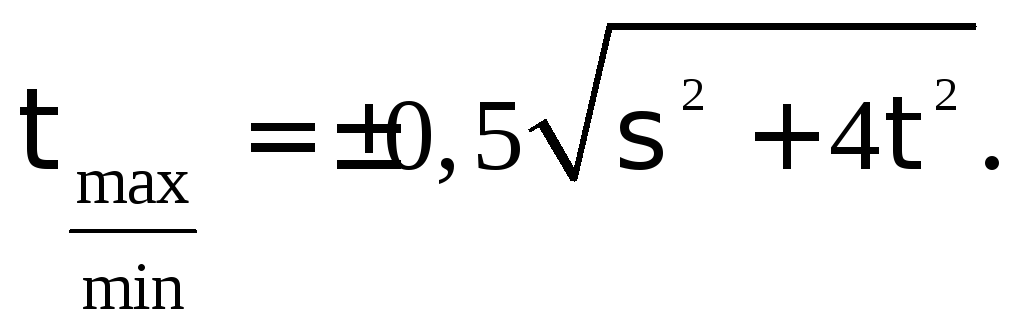 (4.12)
(4.12)

