Метод сил в расчетах статически неопределимых систем

Общие сведения о статически неопределимых системах. Степень статической неопределимости

При изучении курса сопротивления материалов уже приходи­лось встречаться с расчетом статически неопределимых систем, т. е. та­ких, для определения внутренних усилий в которых недостаточно одних лишь уравнений статики: требовалось еще составлять дополнительные уравнения - уравнения деформаций (перемещений).

Характерной особенностью статически неопределимых систем (в отличие от статически определимых) является то, что распределение усилий в них зависит не только от внешних сил, но и от соотношений между поперечными размерами отдельных элементов. Если элементы системы изготовлены из различных материалов, то распределение усилий зависит также от модулей упругости этих материалов. Другая особенность - смещение опор, тем­пературные воздействия и неточность сборки конструкции обычно вызывают появление в таких системах дополнительных усилий, чего не происходит в статически определимых системах.

Расчет статически неопределимой системы начинается с анализа ее схемы. Анализ необходим, прежде всего, для того, чтобы установить сте­пень статической неопределимости.

Степень статической неопределимости равна числу так называемых лиш­них связей, удаление которых превращает статически неопределимую сис­тему в определимую геометрически неизменяемую систему.

Связью в строительной механике называется всякое препятствие, не допускаю­щее изменения взаимного положения точек или сечений системы. Термин «лишняя связь» следует понимать как «избыточная связь», а не как «ненужная связь».

Геометри­чески неизменяемой называется такая система, изменение фор­мы которой возможно лишь в связи с деформациями ее элементов.

Статически определимая система не имеет лишних связей; удаление из нее хотя бы одной связи превращает ее в геометрически изменяемую систему, т.е. в механизм. Балка является системой статически неопределимой один раз (или однажды), если один из опорных стержень­ков представляет собой лишнюю (избыточную) связь ее с землей (с основани­ем). Отбросив один опорный стержень или включив в балку один шарнир, получим статически определимую, геометрически неиз­меняемую систему.

Прямоугольная замкнутая рама является системой трижды статически неопределимой, так как для превращения ее в статически определимую необходимо, например, перерезать один из ее элементов и тем самым устранить три лишние внутренние связи.

Реакциями этих внутренних связей являются: продольная сила, поперечная сила и изгибающий момент, действующие в месте разреза. Эти реакции при помощи уравнений статики не могут быть найдены. В аналогичных условиях в смысле статической неопределимости находится любая система, представ­ляющая замкнутый контур, который всегда трижды статически неопределим.

Примером сооружения с одним замкнутым контуром является система, изобра­женная на рис. 1. Бесшарнирная рама также представляет собой замк­нутый контур; он ограничен снизу землей, которую можно рассматривать как бесконечно жесткий стержень.

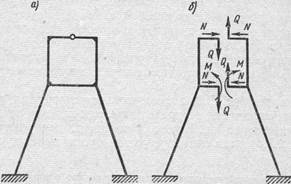
В рамной конструкции, представленной на рис. 2, а, верхний контур снабжен шарниром; в разрезе, проведенном по этому шарниру, действуют только два внутренних усилия: N и Q (рис. 2, 6). Такой контур дважды ста­тически неопределим. Если рассматривать всю систему в целом, то она пять раз статически неопределима, так как нижний контур рамы замкнутый и, следовательно, неопределим трижды. Систему, освобожденную от внутренних лишних связей, можно представить в виде двух защемленных внизу стержней с горизонтальными консолями (рис. 2, 6).

К выяснению степени статической неопределимости этой системы можно подойти и несколько иначе. Верхний контур рамы, имеющий один внутрен­ний шарнир, дважды статически неопределим (имеет две лишние связи). Кроме того, каждая из заделок дает три составляющих опорной реакции (две силы и момент), т. е. на раму наложено шесть внешних связей, а урав­нений статики для плоской системы можно составить лишь три. Следова­тельно, три внешние связи являются лишними, а всего имеется пять лишних связей, т. е. система пять раз статически неопределима.

Необходимо заметить, что исключение лишних связей для превращения одной и той же статически неопределимой конструкции в статически опре­делимую, может быть произведено различными способами, однако число отбрасываемых связей всегда будет одно и то же.

Включение шарнира в узел рамы, в котором сходятся два стержня, или же постановка его в любое место на оси стержня нарушает (снимает) одну связь и снижает общую степень статической неопределимости системы на единицу. Такой шарнир будем называть одиночным, или простым.

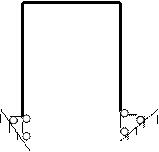
При удалении связей системы необходимо следить за тем, чтобы получае­мая конструкция была геометрически неизменяема. С этой точки зрения в раме, показанной на рис. 3, имеющей одно лишнее опорное закрепление, было бы ошибочным удаление вертикального стерженька, так как оставшиеся три опорных стерженька пересекались бы в точке А и, сле­довательно, не могли бы препятствовать повороту рамы вокруг этой точки. Правильным будет вариант удаления лишнего горизонтального стерженька.

Для конструкций со сложным внутренним образованием можно указать на следующий общий прием определения степени статической неопредели­мости. В его основу кладется то соображение, что каждый шарнир, включен­ный в узел, соединяющий К стержней, снижает степень статической неопре­делимости на К - 1, так как такой шарнир заменяет К - 1 одиночных шарниров. Поэтому для определения степени статической неоп­ределимости конструкции необходимо взять утроенное количество замкну­тых контуров (предполагая, что все шарниры, в том числе и опорные, заме­нены жесткими соединениями) и затем уменьшить его на число включенных в конструкцию одиночных шарниров, учитывая при этом, что один общий шарнир эквивалентен К - 1 одиночным шарнирам. Представив это правило в виде формулы, получим:

Здесь n - степень статической неопределимости системы; m - число замкнутых контуров в конструкции в предположении отсутствия шарнир­ных соединений; Ш - число одиночных шарниров; шарнир, соединяющий два стержня, считается за один (одиночный шарнир), соединяющий три стержня - за два одиночных шарнира (двойной шарнир) и т. д.

Плоскую статически неопределимую систему, имеющую более трех опорных стержней, можно рассматривать как внешне, как внутренне или как одновременно внешне и внутренне статически неопределимую - в зависимости от того, какие связи этой системы считать лиш­ними. Так, например, один раз статически неопределимую раму, изображен­ную на рис. 3, можно рассматривать как внешне статически неопредели­мую, если за лишнюю связь считать правый горизонтальный опорный стер­жень, т. е. если превратить ее в статически определимую систему путем удаления этого стержня. Если же лишней считать связь, препятст­вующую повороту одной части ригеля рамы относительно другой, т. е. пре­вратить раму в статически определимую систему путем постановки шарнира в ригеле, то тогда раму надо рассматривать как внутренне стати­чески неопределимую.

ОСНОВНАЯ СИСТЕМА МЕТОДА СИЛ

Расчет статически неопределимой системы методом сил начинается с определения степени статической неопределимости. Далее нужно выбрать основную систему.

Основная система получается из заданной путем отбрасывания лишних связей. Вместо отброшенных связей прикладываются реакции этих связей. Они называются лишними неизвестными и определяются в процессе расчета статически неопределимой системы.

Основное требование, предъявляемое к основной системе: она должна быть геометрически неизменяемой и статически определимой.

Обычно для заданной системы можно образовать несколько вариантов основной системы. Для расчета выбирают наиболее удобный вариант.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ

Как было указано выше, определение усилий в стати­чески неопределимой системе связано с необходимостью составления до­полнительных уравнений - уравнений деформаций (перемещений) системы. Для этого прежде всего следует превратить заданную п раз стати­чески неопределимую систему в статически определимую, устранив из нее лишние связи. Полученная таким путем статически определимая система называется основной.

Устранение каких-либо связей не изменяет внутренних усилий, возни­кающих в системе, и ее деформаций, если к ней прикладываются дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Поэтому, если к основной системе, кроме заданной нагрузки, приложить реакции устраненных связей, то основная и заданная системы станут эквивалентными.

В заданной системе в направлениях имеющихся жестких связей (в то числе и тех связей, которые отброшены при переходе к основной системе) перемещений быть не может. Поэтому в основной системе перемещения по направлениям отброшенных связей должны быть равны нулю. Следовательно реакции отброшенных связей должны иметь такие значения, при ксторых перемещения по их направлениям равнялись бы нулю.

Условие равенства нулю перемещения по направлению любой из отброшенных связей на основании закона независимости действия сил может быть представлено в следующем виде:

Δ i = Δ i 1 + Δ i 2 + ... +Δ i , n -1 + Δ i n + Δ i p = 0.

Здесь первые индексы означают направление перемещения (и одновременно номер отброшенной связи), а вторые указывают на причины, вызвавшие перемещение. Таким образом, слагаемое Δ ik следует читать: «перемещение по направлению связи i, вызванное действием реакции связи k» Слагаемое Δ ip означает перемещение по направлению связи i, вызванное действием заданной нагрузки.

Обозначив величину реакции связи k (в виде силы или момента) через X k и выразив перемещения Δ ik через единичные перемещения с помощью равенства Δ ik = X k δ ik , представим условие так:

Δ i = X 1 δ i 1 + X 2 δ i 2 + … + X n δ i n + Δ i p = 0.

Таким образом, условие эквивалентности основной и заданной систем математически сводится к удовлетворению системы n линейных уравнений.

Главная Побочные диагонали

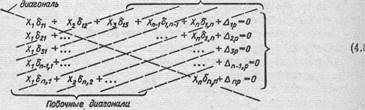
Эти уравнения являются теми дополнительными уравнениями деформаций (перемещений), которые позволяют раскрыть статическую неопределимость заданной системы. Первое из этих уравнений выражает мысль о равенстве нулю перемещения в основной системе по направлению первой отброшенной связи (по направлению силы или момента), второе - по направлению второй отброшенной связи и т. д.

Уравнения называются каноническими уравнениями метода сил. Такое название указывает, во-первых, на то, что уравнения составляются по определенному правилу (канону), и, во-вторых, на то, что неизвестными в уравнениях являются силы, представляющие собой реакции отброшенных связей. Число уравнений равно числу отброшенных связей, т.е. степени статической неопределимости заданной системы.

Следует заметить, что вид канонических уравнений, т. е. количество слагаемых в каждом из них и общее число этих уравнений, определяется лишь степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

Можно установить следующий порядок расчета статически неопределимых систем:

1. Выбирается основная статически оп­ределимая система путем отбрасывания в заданной системе лишних связей.

2. Действие отброшенных связей возме­щается приложением к основной системе неизвестных усилий (сил или моментов).

3. Составляются канонические уравне­ния, выражающие ту мысль, что пол­ные перемещения в основной системе, возникающие по направлениям неизвестных усилий под влиянием этих усилий и нагрузки, равны нулю.

4. Основная система поочередно нагружается единичными усилиями X 1 = 1, Х 2 = 1, …, Х п = 1 и от каждого из них отдельно строятся еди­ничные эпюры изгибающих моментов M i . Помимо этого, строится грузовая эпюра изгибающих моментов М р в основной системе метода сил.

5. Перемножением единичных эпюр вычисляются все коэффициенты δ ik системы канонических уравнений.

6. Перемножением единичных и грузовой эпюр определяются грузовые члены Δ ip системы канонических уравнений.

7. Решается система канонических уравнений, в результате чего находятся значения неизвестных Х 1 , Х 2 , …, Х n .

8. Для получения окончательной (суммарной) эпюры изгибающих моментов ординаты каждой из единичных эпюр умножаются на найденное значение соответствующего неизвестного и все результаты суммируются (по отдельным точкам осей системы) с добавлением к ним ординат грузовой эпюры моментов. В ходе расчета выполняются проверки.

МАТРИЧНАЯ ФОРМА МЕТОДА СИЛ

Запишем канонические уравнения метода сил для n раз статически неопределимой системы:

δ 11 X 1 + δ 12 X 2 + … +δ 1 n X n + Δ 1 p = 0

δ 21 X 1 + δ 22 X 2 + … +δ 2 n X n + Δ 2 p = 0

δ n 1 X 1 + δ n 2 X 2 + … +δ nn X n + Δ np = 0

В – матрица податливости системы.

Вектор р также можно определить по матричной формуле:

Р = L x В р,

где р – вектор изгибающих моментов в основной системе от внешней нагрузки.

= – (L x T BL x) -1 ×L x T B р.

После определения вектора можно найти изгибающие моменты для заданной системы по следующей формуле:

где – изгибающий момент для заданной системы.

Полученные формулы применяются при расчете рам методом сил с помощью ЭВМ.

Исходными для расчета являются следующие три матрицы: L x , В, р.

РАСЧЕТ РАМ МЕТОДОМ СИЛ С ПОМОЩЬЮ ЭВМ

Порядок расчета:

1. Определить степень статической неопределимости и выбрать основную систему.

2. Разбить раму на участки, нанести и пронумеровать сечения и выбрать правило знаков изгибающих моментов.

3. Построить эпюры изгибающих моментов в единичных и грузовом состояниях основной системы.

4. По единичным эпюрам составить матрицу L x . Число строк в этой матрице равно числу сечений, а число столбцов равно числу единичных состояний основной системы.

5. По грузовой эпюре составить вектор р.

6. Составить матрицы податливости для отдельных участков рамы, а затем для рамы в целом (матрица В).

7. С помощью ЭВМ (программа RAMS) найти вектор и построить эпюру изгибающих моментов для заданной системы.

8. Выполнить первую статическую проверку (SМ уз = 0).

9. Построить эпюры поперечных сил Q и продольных сил N.

10. Выполнить вторую статическую проверку, т.е. проверку равновесия рамы в целом (SХ = 0; SУ = 0).

Примечание. Кинематическая проверка (проверка отсутствия перемещений по тем направлениям, где они заведомо отсутствуют) выполняется в процессе расчета самой ЭВМ.

Статически неопределимыми системами называются стержневые системы, для определения реакций опор в которых только уравнений равновесия недостаточно. С кинематической точки зрения это такие стержневые системы, число степеней свободы которых меньше числа связей. Для раскрытия статической неопределимости таких систем необходимо составлять дополнительные уравнения совместности деформаций. Число таких уравнений определяется числом статической неопределимости стержневой системы. На рис.8.14 приведены примеры статически неопределимых балок и рам.

Балка, изображенная на рис.8.14б, называется неразрезной балкой. Происходит это название оттого, что промежуточная опора лишь подпирает балку. В месте опоры балка не разрезана шарниром, шарнир не врезан в тело балки. Поэтому влияние напряжений и деформаций, которые балка испытывает на левом пролете, сказываются и на правом пролете. Если в месте промежуточной опоры врезать шарнир в тело балки, то в результате система станет статически определимой  из одной балки мы получим две независимые друг от друга балки, каждая из которых будет статически определимой. Следует отметить, что неразрезные балки являются менее материалоемкими по сравнению с разрезными, так как более рационально распределяют изгибающие моменты по своей длине. В связи с этим неразрезные балки получили широкое применение в строительстве и машиностроении. Однако, неразрезные балки, будучи статически неопределимыми, требуют специальной методики расчета, включающей в себя использование деформаций системы.

Прежде, чем приступать к расчету статически неопределимых систем, необходимо научиться определять степень их статической неопределимости. Одним из наиболее простых правил определения степени статической неопределимости является следующее:

, (8.3)

где  число связей, накладываемых на конструкцию;  число возможных независимых уравнений равновесия, которые можно составить для рассматриваемой системы.

Воспользуемся уравнением (8.3) для определения степени статической неопределимости систем, изображенных на рис 8.14.

Балка, изображенная на рис 8.14а, является один раз статически неопределимой, так как имеет три связи на левой опоре и одну связь на правой опоре. Независимых уравнений равновесия для такой балки можно составить только три. Таким образом, степень статической неопределимости балки

. Неразрезная балка, изображенная на рис 8.14б также один раз статически неопределима, так как обладает двумя связями на левой опоре и по одной связи на промежуточной опоре и на правой опоре – всего четыре связи. Таким образом, степень ее статической неопределимости

.

Рама, изображенная на рис. 8.14в, три раза статически неопределима, так как обладает шестью связями в опорах. Независимых уравнений равновесия для этой рамы можно составить только три. Таким образом, степень статической неопределимости для этой рамы из уравнения (8.3) равна:

. Степень статической неопределимости рамы, изображенной на рис.8.18,г равна четырем, так как рама обладает семью связями на опорах. Следовательно, степень ее статической неопределимости равна

.

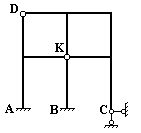
Правило (8.3) для определения степени статической неопределимости применяют только для простых систем. В более сложных случаях это правило не работает. На рис 8.15 представлена рама, степень статической неопределимости которой, пользуясь уравнением (8.3), определить невозможно.

Внешне, система, приведенная на рис 8.15, пять раз статически неопределима. Это легко установить с помощью уравнения (8.3): из шести внешних связей (три в сечении А, три в сечении В и два в сечении С) вычитаются три возможные уравнения равновесия. Однако, эта система обладает еще и внутренней статической неопределимостью. Учесть внутреннюю статическую неопределимость с помощью уравнения (8.3) нельзя. Прежде, чем перейти к определению степени статической неопределимости рамы, изображенной на рис 8.15, введем несколько определений. Первое из этих определений включает в себя понятие о простом шарнире.

Простым называется шарнир, соединяющий два стержня (Рис.8.16).

Рис.8.16. Простой шарнир

Шарнир, соединяющий несколько стержней, называется сложным (Рис.8.17).

Рис.8.17. Сложный шарнир

Число простых шарниров, которые могут заменить один сложный шарнир, определим из формулы:

, (8.4)

где

 число стержней, входящих в узел.

Пересчитаем сложный шарнир, изображенный на рис.8.17 в число простых шарниров с помощью формулы (8.4):

. Таким образом, сложный шарнир, изображенный на рис.8.17, можно заменить четырьмя простыми шарнирами.

Введем еще одно понятие  замкнутый контур .

Докажем теорему: любой замкнутый контур три раза статически неопределим.

Для доказательства теоремы рассмотрим замкнутый контур, нагруженный внешними силами (Рис.8.18).

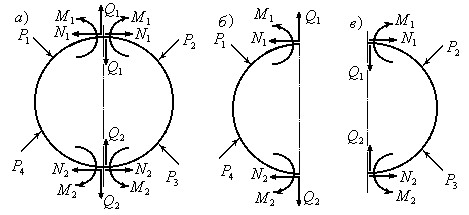
Разрежем замкнутый контур вертикальным сечением и покажем внутренние силовые факторы, возникающие в месте сечения. В каждом из сечений возникают три внутренних фактора: поперечная сила , изгибающий момент

и продольная сила

. Всего на каждую из отсеченных частей контура кроме внешних сил действуют шесть внутренних факторов (Рис.8.18,б,в). Рассматривая равновесие одной из отсеченных частей, например, левой (Рис.8.18,б), выясняем, что задача три раза статически неопределима, так как для отсеченной части можно составить всего три независимых уравнения равновесия, а неизвестных сил, действующих на отсеченную часть, шесть. Таким образом, степень статической неопределимости замкнутого контура равна

. Теорема доказана.

Теперь, используя понятие о простом шарнире и замкнутом контуре, можно сформулировать еще одно правило для определения степени статической неопределимости:

, (8.5)

где

 число замкнутых контура;

 число шарниров в пересчете на простые (8.4).

Пользуясь уравнением (8.5), определим степень статической неопределимости рамы, изображенной на рис 8.15. Рама имеет пять контуров

, включая контур, образуемый опорными стержнями. Шарнир в узле D простой, так как соединяет два стержня. Шарнир в сечении К – сложный, так как соединяет четыре стержня. Число простых шарниров, которые могли бы заменить шарнир в сечении К, равно по формуле (8.4):

. Шарнир С также является сложным, так как соединяет три стержня. Для этого шарнира

. Кроме того, система имеет еще два простых шарнира, с помощью которых крепится к основанию. Таким образом, число простых шарниров в системе равно

. Подставляя число замкнутых контуров

и число простых шарниров

в формулу (8.5) определяем степень статической неопределимости рамы:

. Таким образом, изображенная на рис. 8.15 рама, семь раз статически неопределима. А это означает, что для расчета подобной системы необходимо составить дополнительно к трем уравнениям равновесия семь уравнений совместности деформаций. Решая полученную таким образом систему из 10 уравнений относительно неизвестных, входящих в эти уравнения, можно определить как величины реакций во внешних связях, так и внутренние усилия, возникающие в раме. Процедуру решения этой задачи можно несколько упростить, исключив из системы уравнений уравнения равновесия. Однако такой подход требует применения специальных методов решения, одним из которых является метод сил.

6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ

6.1. Анализ структуры стержневых систем

Пусть N - степень статической неопределимости системы. Для систем без замкнутых контуров (рис. 6.1,а) N=R - 3, где R - число реакций. Для конструкций с замкнутыми контурами (рис. 6.1,б) N=3K-Ш, где K - число замкнутых контуров, Ш - число простых одиночных шарниров, таких, которые соединяют в шарнире два элемента. При добавлении в шарнире еще одного элемента, число Ш увеличивается на единицу.

Так как статически неопределимую систему непосредственно рассчитать не удается, превратим ее в статически определимую систему. Основной системой называется статически определимая система, полученная из статически неопределимой (рис. 6.1,а), отбрасыванием Рис. 6.2

опорных связей (рис. 6.2,а), проведением разрезов (рис. 6.2,б), введением шарниров (рис. 6.2,в) или комбинацией этих способов.

Полученная основная система должна быть геометрически неизменяема, то есть ее элементы не должны перемещаться без их деформации. На рис. 6.2,д изображена геометрически изменяемая основная система, полученная из статически неопределимой системы (рис. 6.2,г). Частным случаем геометрически изменяемой системы является мгновенно изменяемая система (рис. 6.2,е).

Основная система, к которой приложена заданная нагрузка и неизвестные пока реакции отброшенных связей или внутренние силы называется эквивалентной системой.

8.2 Канонические уравнения метода сил

Введем обозначения:

· Dmn - перемещение по направлению mтой силы (момента) от nтой нагрузки.

· DmF - перемещение по направлению mтой силы (момента) от заданной нагрузки, называемое грузовым перемещением.

· dmn - перемещение по направлению mтой единичной силы (момента) от nтой единичной нагрузки, называемое единичным перемещением.

· Amn – работа mтой силы (момента) на перемещении по ее направлению, вызванном nтой нагрузкой.

http://pandia.ru/text/79/031/images/image004_68.gif" width="47" height="25">, от нее перемещение равно d11, а от силы X1 будет d11×X1. Найдем вертикальное перемещение от силы X2..gif" width="47" height="27 src=">, от нее перемещение равно d13: а от X3 будет d13×X3. Используем принцип суперпозиции.

Рис. 6.3 Тогда полное вертикальное перемещение точки C за-

http://pandia.ru/text/79/031/images/image008_36.gif" width="383" height="34 src=">,

http://pandia.ru/text/79/031/images/image010_29.gif" width="419" height="133 src="> (6.1)

Коэффициенты dii называются главными - dii > 0, коэффициенты diк (i ¹ k) называются побочными diк >< 0.

Теорема о взаимности работ

DIV_ADBLOCK2">

6. Подставляем найденные единичные и грузовые коэффициенты в систему канонических уравнений метода сил, решаем ее и находим значения « лишних » неизвестных.

7. Рассматриваем выбранную эквивалентную систему с найденными значениями « лишних » неизвестных.

8. Находим внутренние усилия в элементах выбранной эквивалентной системы и строим их эпюры.

9. Проводим статическую проверку равновесия узлов конструкции и кинематическую проверку – вычисляем перемещения выбранной эквивалентной системы по направлению отброшенных связей. Эти перемещения должны отсутствовать.

10. Проводим проверку элементов статически неопределимой конструкции на прочность.

7. ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ, ЦИКЛИЧЕСКИ ИЗМЕНЯЮЩИХСЯ ВО ВРЕМЕНИ

7.1. Механизм усталостного разрушения

Действиям циклических напряжений подвергается материал во многих конструкциях. При этом, несмотря на то, что значение возника-ющих максимальных напряжений меньше предела прочности, спустя некоторое время при действии переменного напряжения в конструкции возникают трещины, и она разрушается. Если рассмотреть место разру-шения (рис. 7.1), то можно увидеть гладкую (блестящую) зону 1 распро - странения усталостной трещины и зернистую зону 2 хрупкого разрушения ослабленного сечения.

http://pandia.ru/text/79/031/images/image013_24.gif" align="left" width="145" height="150">

Рис. 7.1 Рис. 7.2

Микротрещины возникают в тех точках, где напряжения максимальны. Постепенно они сливаются в одну трещину, уменьшая при этом размер сечения конструкции, соответственно возрастает максимальное напряжение, и при достижении предельного напряжения, конструкция хрупко разрушается. Распространение трещины связывают с изменением структуры материала и называют - усталостью. Способность сопротивляться усталости называют выносливостью материала. Время от начала нагружения, до появления усталостной трещины, значительно больше времени, прошедшего от возникновения трещины до разрушения конструкции.

При рассмотрении периодической циклической нагрузки обычно огра-ничиваются синусоидальным законом изменения напряжений (рис. 7.2).

Здесь Т – время цикла или цикл; http://pandia.ru/text/79/031/images/image015_23.gif" width="123" height="45 src="> - среднее напряжение и амплитуда переменного напряжения (цикла) ;

и - максимальное и минимальное напря-жения цикла.

Для характеристики циклов нагружения используются коэффициент асимметрии цикла или характеристика цикла .

Два цикла с одинаковыми r (или равными k) – называются подобными.

Если , то цикл называется симметричным.

Если , то цикл называется асимметричным, в частности,

если http://pandia.ru/text/79/031/images/image024_22.gif" align="left" width="239" height="134 src="> При испытании материалов на вы-носливость обычно применяют цилиндри-ческие полированные образцы диаметром мм, длиной 70 – 100 мм. Приклады-вают к ним напряжения, изменяющиеся по заданному циклу, и определяют число

циклов до разрушения при данном smax.

Рис. 7.3. Каждой паре значений smax и N соответствует точка (рис. 7.3), соединяя которые получим кривую, называмую кривой усталости или кривой Веллера.

Пределом выносливости sr - называется максимальное напряжение цикла, при котором материал не разрушается при бесконечно большом числе циклов. Для большинства материалов не удается установить такое число циклов, пройдя которое, при дальнейшем испытании материал бы не разрушился (цветные металлы, легированные стали , пластмассы). В этом случае вводят условный предел выносливости - s-1N при базовом числе циклов N0 , например, для цветных металлов и их сплавов N0=108 циклов.

При симметричном цикле предел выносливости обозначается σ-1.

Для обычных сталей s-1 » (0.4¸0..gif" width="90" height="56">..gif" width="49" height="24"> .

Влияние абсолютных размеров. Учитывается масштабным фактором

: . Здесь s-1Д – предел выносливости образца заданного размера. Чем больше размер образца, тем предел выносливости ниже.

Влияние качества обработанной поверхности. У читывается коэффи-циентом качества поверхности ; . - предел выносли-вости образца с заданной обработкой поверхности. При этом учитывается влияние механической (точение, шлифование, полировка, накатывание, дробеструйная обработка), термической (закалка, отпуск), химической (азортирование) и других видов обработки поверхности.

http://pandia.ru/text/79/031/images/image035_15.gif" align="left" width="348" height="173 src="> Влияние вида цикла изменения напряжений. Для этого построем диа-грамму усталостной прочности материала. При испытаниях задаем sm и путем подбора определяем такую величину sa, при котором материал выдерживает базовое число циклов нагружения.. Откладываем эти точки при разных r (рис. 7.4) и получаем диаграмму предельных амплитуд.

Рис. 7.4 Рис. 7.5

Затем, для действующего на деталь цикла напряжений, находим и sm и откладываем рабочую точку Е. Через начало координат и рабочую точку проведем луч ОЕ, на котором расположены все циклы, подобные дейст-вующему. Луч пересекает диаграмму предельных амплитуд в точке D, которой соответствует предельный подобный цикл. Если точка Е лежит на отрезке OD, то деталь выдержит число циклов нагружения, равное или большее базового числа циклов, а если за точкой D - то разрушение произойдет при числе циклов, меньшем, чем базовое..gif" width="75" height="49"> называется запасом усталостной прочности или коэффициентом запаса прочности по выносливости.

Такие испытания достаточно дороги и продолжительны. Поэтому применяют упрощенные – схематизированные диаграммы. Простейшая такая схематизация состоит в том, что кривую диаграммы усталой проч-ности заменяют прямой AB (рис. При этом погрешность определе-ния коэффициента запаса прочности по выносливости идет в запас проч-ности детали. Иногда применяют более точную диаграмму (рис. 7.5), построенную по трем сериям испытаний образцов при действии постоян-ной нагрузки, симметричном и пульсирующем циклах.

Формула, по которой находится коэффициент запаса усталостной прочности, зависит от выбранной схематизированной диаграммы. Учиты-вая влияние перечисленных выше факторов на величину предела вынос-ливости, можно получить

http://pandia.ru/text/79/031/images/image039_12.gif" align="left" width="145" height="58 src=">.gif" align="left" width="98" height="55 src=">.gif" align="left" width="77" height="58 src=">.gif" width="95" height="52 src=">

и коэффициент запаса усталостной прочности в предположении, что s = 0.

http://pandia.ru/text/79/031/images/image047_11.gif" width="127" height="61">.

Кроме вычисления коэффициента запаса усталостной прочности, должен быть найден коэффициент запаса статической прочности.

8. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ

ДЕФОРМИРУЕМЫХ СИСТЕМ

8.1. Устойчивые и неустойчивые системы

Устойчивость систем можно проиллюстрировать рисунками (На (рис.8.1,а) изображена устойчивая система, на (рис. 8.1,б) - неустойчивая, на (рис.8.1,в) - безразличная, и на (рис.8.1,г) - устойчивая “в малом”, но не устойчивая “в большом”.

Бифуркация" href="/text/category/bifurkatciya/" rel="bookmark">бифуркацией , а силы, действующие на систему в этот момент, - критическими http://pandia.ru/text/79/031/images/image050_9.gif" width="82" height="51 src=">.

Здесь ny - коэффициент запаса устойчивости.

При F = FКР в конструкции возникают критические напряжения http://pandia.ru/text/79/031/images/image052_10.gif" width="87" height="47 src=">.

8.2. Задача Эйлера

Пусть стержень сжимается силой http://pandia.ru/text/79/031/images/image053_11.gif" width="19" height="22"> достигнет критического значения , то стержень изогнется. Используем приближенное дифференциальное уравнение изогнутой оси балки при малых деформациях http://pandia.ru/text/79/031/images/image056_10.gif" width="94" height="28 src=">.gif" width="120" height="27 src=">, или , где http://pandia.ru/text/79/031/images/image061_8.gif" align="left" width="314" height="207 src="> Общий интеграл этого дифференциального уравнения имеет вид:

http://pandia.ru/text/79/031/images/image063_7.gif" width="42" height="22 src=">.gif" width="45" height="21">;

при http://pandia.ru/text/79/031/images/image067_6.gif" width="43" height="20 src=">, то есть ..gif" width="45" height="20">, то , то есть стержень прямой, что противоречит условию задачи.

Значит, http://pandia.ru/text/79/031/images/image073_9.gif" width="61" height="22 src=">.gif" width="185" height="51 src=">.

При , http://pandia.ru/text/79/031/images/image077_6.gif" width="256" height="49 src=">.

При получим минимальное значение критической силы .

Надо учесть, что потеря устойчивости происходят в направлении наименьшей жесткости, перпендикулярно плоскости, проходящей через ось стержня и главную центральную ось, относительно которой http://pandia.ru/text/79/031/images/image081_5.gif" width="118" height="51 src=">. В уравнении прогибов величина осталась неизвестной, но она должна быть достаточно мала, чтобы можно было воспользоваться приближенным дифференциальным уравнением изогнутой оси балки. Случаи и так далее без дополнительных опор при статическом действии нагрузки не реализуются.

8.3. Влияние способов закрепления концов стержня

на величину критической силы

свел различные случаи опирания стержня к случаю шарнирного опирания на концах и ввел так называемую « приведенную » длину (рис. Здесь – « приведенная » длина, - коэффициент приведения длины.

http://pandia.ru/text/79/031/images/image088_4.gif" width="118" height="55 src="> .

Определяем критические напряжения

http://pandia.ru/text/79/031/images/image090_3.gif" width="69" height="52 src="> называется гибкостью стержня.

В выводе формулы для критических сил и напряжений, использовалось приближенное дифференциальное уравнение изогнутой оси балки. Это уравнение было выведено в предположении, что материал стержня подчиняется закону Гука. Таким образом, полученные зависимости можно применять только для значений напряжений, меньших или равных пределу пропорциональности

http://pandia.ru/text/79/031/images/image092_4.gif" width="90" height="64">. Обозначим .

Таким образом, формула Эйлера может применяться при .

Определение критических напряжений для стержней, у которых меньше проводится с помощью экспериментов.

Разделим стержни на три категории по их гибкости:

1..gif" width="160" height="31 src=">.

3..gif" width="34" height="28">.gif" width="26" height="28">- для хрупких материалов.

В стержнях средней гибкости на несущую способность влияют как пластические деформации, так и потеря устойчивости. Для стержней малой и средней гибкости на основе экспериментов предложил формулу 0 " style="margin-left:14.4pt;border-collapse:collapse;border:none">

Для решения большинства статически неопределимых встречающихся на практике задач обозначенные приемы оказываются, однако, далеко не достаточными. Поэтому необходимо остановиться на более общих методах раскрытия статической неопределимости на примере стержневых систем.

Под стержневой системой в широком смысле слова понимается всякая конструкция, состоящая из элементов, имеющих форму бруса. Если элементы конструкции работают в основном на растяжение или сжатие, то стержневая система называется фермой (рис. 1).

Рис.1. Расчетная схема формы

Ферма состоит из прямых стержней, образующих треугольники. Для формы характерно приложение внешних сил в узлах.

Если элементы стержневой системы работают в основном на изгиб или кручение, то система называется рамой (рис. 2).

Особую, наиболее простую для исследования группу стержневых систем составляют плоские системы. У плоской рамы или фермы оси всех составляющих элементов до и после деформации расположены в одной плоскости. В этой же плоскости действуют все внешние силы, включая и реакции опор (см. рис. 2,а ).

Наряду с плоскими рассматриваются так называемые плоско-пространственные системы. Для такого рода систем оси составляющих элементов в недеформированном состоянии располагаются, как и для плоских систем, в одной плоскости. Внешние же силовые факторы действуют в плоскостях, перпендикулярных к этой плоскости (рис. 2,в) . Стержневые системы, не относящиеся к двум указанным классам, называются пространственными (рис.2,в ).

Рамы и фермы принято разделять на статически определимые и статически неопределимые . Под статически определимой понимается такая кинематически неизменяемая система, для которой все реакции опор могут быть определены при помощи уравнений равновесия, а затем при найденных опорных реакциях методом сечений могут быть найдены также и внутренние силовые факторы в любом поперечном сечении. Под статически неопределимой системой имеется в виду такая, опять же кинематически неизменяемая система, для которой определение внешних реакций и внутренних силовых факторов не может быть произведено при помощи метода сечений и уравнений равновесия.

а) плоская, б) плоскопространственная. в) пространственная

Рис.2. Расчетные схемы рамных конструкций:

Разность между числом неизвестных (реакций опор и внутренних силовых факторов) и числом независимых уравнений статики, которые могут быть составлены для рассматриваемой системы, носит название степени или числа статической неопределимости . В зависимости от этого числа системы разделяются на один, два, три...., n раз статически неопределимые. Иногда говорят, что степень статической неопределимости равна числу дополнительных связей, наложенных на систему. Остановимся на этом вопросе подробнее.

Положение жесткого бруса в пространстве определяется шестью независимыми координатами, иначе говоря, жесткий брус обладает шестью степенями свободы. На брус могут быть наложены связи, т. е. ограничения, обусловливающие его определенное положение в пространстве. Наиболее простыми связями являются такие, при которых полностью исключается то или иное обобщенное перемещение для некоторых сечений бруса. Наложение одной связи снимает одну степень свободы с бруса как с жесткого целого. Следовательно, если на свободный жесткий брус наложено шесть связей, то положение его в пространстве как жесткого целого будет, за некоторыми исключениями, определено полностью и система из механизма, обладающего шестью степенями свободы, превращается в кинематически неизменяемую систему. То число связей, при котором достигается кинематическая неизменяемость, носит название необходимого числа связей . Всякую связь, наложенную сверх необходимых, называют дополнительной . Число дополнительных связей равно степени статической неопределимости системы.

Связи в рамах и стержневых системах делят обычно на связи внешние и связи внутренние, или взаимные. Под внешними связями понимаются условия, накладываемые на абсолютные перемещения некоторых точек системы.

а)внешняя связь, б) две внешние связи в) шесть внешних связей в общем случае

Рис.3. Схемы эквивалентных связей

Если, например, на левый конец бруса (рис. 3, а ) наложено условие, запрещающее вертикальное перемещение, говорят, что в этой точке имеется одна внешняя связь. Условно она изображается в виде двух шарниров или катка. Если запрещено как вертикальное, так и горизонтальное смещение, говорят, что наложены две внешние связи (рис. 3, б ). Заделка в плоской системе дает три внешние связи. Пространственная заделка соответствует шести внешним связям (рис. 3, б ). Внешние связи часто, как уже упоминалось, делят на необходимые и дополнительные. Например, на рис. 4, а и б показана плоская рама, имеющая в первом случае три внешние связи, а во втором - пять внешних связей. Для того чтобы определить положение рамы в плоскости как жесткого целого, необходимо наложение трех связей. Следовательно, в первом случае рама имеет необходимые внешние связи, а во втором, кроме того, две дополнительные внешние связи.

а) три внешних связи, б) пять внешних связей

Рис.4. Плоская рама

Под внутренними, или взаимными, связями понимаются ограничения, накладываемые на взаимные смещения элементов рамы. Здесь также можно говорить как о необходимых, так и о дополнительных связях. Так, например, плоская рама, показанная на рис. 5, а , имеет необходимое количество как внешних, так и внутренних связей между элементами. Это - кинематически неизменяемая система. Если будут заданы внешние силы, мы сможем найти как реакции опор, так и внутренние силовые факторы в любом поперечном сечении рамы. В той же раме, показанной на рис. 5, б , дополнительно наложены две дополнительные внутренние связи, запрещающие взаимное вертикальное и горизонтальное смещения точек А и В . Система в данном случае дважды статически неопределима (иногда добавляют: «внутренним образом»).

В раме рис. 4, а и б также имеются внутренние дополнительные связи. Контур рамы полностью замкнут. Разрезая его в любом сечении (рис.5 в), мы, не нарушая кинематической неизменяемости, получаем возможность при заданных силах найти внутренние силовые факторы в каждом сечении рамы. Следовательно, разрезая замкнутую раму, мы снимаем дополнительные связи, т.е. позволяем сечениям А и В поворачиваться и смещаться в двух направлениях друг относительно друга. Обобщая, можно сказать, что замкнутый плоский контур имеет три дополнительные взаимные связи- трижды статически неопределим. Таким образом, рама, показанная на рис. 4, а , трижды статически неопределима. Рама, показанная на рис. 4, б , пять раз статически неопределима (три раза внутренним образом и два раза - внешним).

а) кинематически неизменяемая, б) неопределимая внутренним образом, в)со снятием дополнительных связей

Рис.5. Классификационные признаки рам:

Рассмотрим теперь несколько примеров определения степени статической неопределимости стержневых и рамных систем. На рис. 6 показано несколько рам. Последовательно рассмотрим их.

а) Рама имеет четыре дополнительные внешние связи и три взаимные связи, т. е. семь раз статически неопределима.

б) Полагаем сначала, что шарнир А отсутствует. Тогда имеются две внешние и три внутренние дополнительные связи. Система без шарнира А была бы пять раз статически неопределимой.

Шарнир А принадлежит одновременно трем стержням. Его можно рассматривать как два совпавших шарнира (рис. 7). Так как каждый шарнир снимает одну связь, т. е. разрешает поворот одного сечения относительно другого, то можно сказать, что шарнир А снимает две связи. Система становится, таким образом, вместо пяти - три раза статически неопределимой.

Обобщая сказанное, можно сделать вывод, что шарнир снимает число связей, на единицу меньшее числа сходящихся в нем стержней. В данном случае в шарнире А сходятся три стержня и шарнир снимает две связи.

а) статически неопределимая - семь, б) - три, в) - четыре, г) - три, е) - двенадцать,
ж) - семь, д) - три, и) - тринадцать раз статически неопределима

Рис.6. Примеры рамных конструкций:

в) Если бы шарнир А отсутствовал, система была бы четыре раза внешним образом и три раза внутренним образом статически неопределимой, т. е. всего семь раз. Шарнир А снимает число связей, на единицу меньшее числа сходящихся в нем стержней, т. е. три связи. Рама четыре раза статически неопределима.

г) Рама три раза статически неопределима.

д) Внешние связи не удовлетворяют условиям кинематической неизменяемости. Это - механизм, точнее говоря, мгновенный механизм. Система имеет возможность поворачиваться относительно верхней опоры как жесткое целое Понятно, что угол поворота будет небольшим. Нижняя связь заклинится и будет достигнуто какое-то положение равновесия, но новое положение связей будет зависеть от жесткости системы. К раме неприменимы основные принципы сопротивления материалов: принцип неизменности начальных размеров и принцип независимости действия сил.

Рис.7. модель двух совпадших шарниров

е) Рама - пространственная. Имеется шесть дополнительных внешних связей (лишняя заделка) и шесть дополнительных взаимных связей (замкнутый контур) Система 12 раз статически неопределима.

ж) Система семь раз статически неопределима (один раз внешним образом и шесть раз - внутренним).

з) Здесь для плоской рамы не показаны внешние связи, но дана система внешних сил, удовлетворяющая условиям равновесия. В таком случае условились считать, что дополнительных внешних связей нет, и положение рамы в пространстве считается определенным; рассматриваются только внутренние связи. Система три раза статически неопределима.

и) Здесь также рассматриваются только внутренние связи, поскольку система указанных внешних сил удовлетворяет условиям равновесия. Нужно подсчитать, сколько сечений необходимо сделать в раме, чтобы, с одной стороны, она не «рассыпалась», а с другой, чтобы в ней не осталось ни одного замкнутого контура. Таких сечений следует сделать пять (см. рис. 6, и ). Система 30 раз статически неопределима.

Лекция № 38. Метод сил.

Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил . Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил». Такой прием не является единственно возможным. В строительной механике широко применяются и другие методы, например метод деформаций, в котором за неизвестные принимаются не силовые факторы, а перемещения в элементах стержневой системы.

Итак, раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы .

а-д) модификации основной системы
Рис.1. пример стержневой рамы:

Для каждой статически неопределимой стержневой системы можно подобрать, как правило, сколько угодно основных систем. Например, для рамы, показанной на рис. 1, можно предложить основные системы, а ), б ),..., которые получены путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с тем нужно помнить, что не всякая система с семью отброшенными связями может быть принята как основная. На рис. 2 показано три примера для той же рамы, в которой также отброшено семь связей, однако сделано это неправильно, так как оставшиеся связи не обеспечивают кинематической неизменяемости системы, с одной стороны, и статической определимости во всех узлах,- с другой.

Рис.2. Некорректные преобразования заданной системы в основные по причине кинематической изменяемости- а) б), или статической определимости во всех узлах - в)

После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо, как уже говорилось, ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать X i -, где i - номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы X i , - являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

а)-д) по отношению к заданной системе
Рис.3. Пять разновидностей основных систем

Основная система, к которой приложены все внешние заданные силы и неизвестные силовые факторы, носит название эквивалентной системы . На рис. 3 показано пять эквивалентных систем, которые соответствуют приведенным выше основным системам (рис. 1). Принцип приложения неизвестных силовых факторов становится ясным без дальнейших пояснений.

Теперь остается составить уравнения для определения неизвестных.

Обратимся к некоторому конкретному примеру. Рассмотрим, например, первую эквивалентную систему из числа представленных на рис. 3,4. Тем, что рассматривается конкретно взятая семь раз статически неопределимая система, общность рассуждений не будет нарушена.

Перейдем теперь к составлению уравнений для определения неизвестных силовых факторов. Условимся через обозначать взаимное смещение точек системы.

Рис.4. Пример расчета рамы а)по выбранной основной системе- б)

Первый индекс при соответствует направлению перемещения, а второй - силе, вызвавшей это перемещение.

В рассматриваемой раме в точке А отброшена неподвижная опора. Следовательно, горизонтальное перемещение здесь равно нулю и можно записать:

Индекс 1 означает, что речь идет о перемещении по направлению силы Х 1 , а индекс [Х 1 , Х 2 ,..., Р ] показывает, что перемещение определяется суммой всех сил, как заданных, так и неизвестных.

Аналогично можно записать:

Так как под величиной понимается взаимное смещение точек, то обозначает вертикальное смещение точки В относительно С , - горизонтальное взаимное смещение тех же точек, есть взаимное угловое смещение сечений В и С . Угловым смещением будет также в рассматриваемой системе величина .

В точках A и D смещения являются абсолютными. Но абсолютные смещения можно рассматривать как смещения, взаимные с неподвижными отброшенными опорами. Поэтому принятые обозначения приемлемы для всех сечений системы.

Пользуясь принципом независимости действия сил, раскроем выражения для перемещений

Аналогичным образом запишем и остальные пять уравнений: каждое из слагаемых , входящих в уравнение, обозначает перемещение в направлении силы с первым индексом под действием силы, стоящей во втором индексе. Поскольку каждое перемещение пропорционально соответствующей силе, величину можно записать в следующем виде:

Что касается перемещений , и т. д., то под индексом Р будем понимать не просто внешнюю силу Р , а вообще систему внешних сил, которая может быть произвольной Поэтому величины , ,... в уравнениях оставим неизменными.

Теперь уравнения примут вид:

Эти уравнения являются окончательными и носят название канонических уравнений метода сил . Число их равно степени статической неопределимости системы. В некоторых случаях, как увидим далее, когда имеется возможность сразу указать значения некоторых неизвестных, число совместно решаемых уравнений снижается. Остается теперь выяснить, что представляют собой коэффициенты и как следует их определять. Для этого обратимся к выражению (6.1).

Следовательно, коэффициент это есть перемещение по направлению i -го силового фактора под действием единичного фактора, заменяющего k -й фактор. Например, коэффициент уравнения представляет собой взаимное горизонтальное смещение точек B и С , которое возникло бы в раме, если бы к ней вместо всех сил была приложена только единичная сила в точке А (рис. 5 а). Если, например, вместо сил приложив единичные силы, а все прочие силы с эквивалентной системы снять (рис. 5 б), то угол поворота в сечении D под действием этих сил будет , горизонтальное перемещение в точке А будет и т. д.

а) , б) и
Рис.5. Интерпретация коэффициентов уравнений метода сил:, а с другой стороны, из теоремы о взаимности перемещений, поскольку перемещения

Раскрытие статической неопределимости на этом заканчивается.

Рис.8. Суммарная эпюра изгибающих моментов.

Эпюра изгибающих моментов может быть получена наложением на эпюру моментов заданных сил трех единичных эпюр, увеличенных соответственно в , и раза Суммарная эпюра изгибающих моментов представлена на рис. 8. Там же пунктиром показана форма изогнутой оси рамы.

Лекция № 39. Расчет толстостенных цилиндров.

В тонкостенных цилиндрических резервуарах, подвергнутых внутреннему давлению, вполне возможно при вычислениях считать напряжения равномерно распределенными по толщине стенки. Это допущение мало отзывается на точности расчета.

В цилиндрах, у которых толщина стенок не мала по сравнению с радиусом, подобное предположение повело бы к большим погрешностям. Расчет таких цилиндров дан Ляме и Гадолиным в 1852 - 1854 гг. Работы русского академика А. В. Гадолина в области расчета кривых стержней в применении к расчету прочности артиллерийских орудий создали ему мировую известность. Отечественные артиллерийские заводы (и многие зарубежные) до сих пор проектируют и изготовляют орудия, пользуясь исследованиями Гадолина.

АВ , a - напряжения по его боковым граням. По симметрии сечения цилиндра и действующей нагрузки элемент АВ перекашиваться не будет, и касательные напряжения по его граням будут отсутствовать. По граням элемента AB , совпадающим с плоскостью чертежа, будет действовать третье главное напряжение , вызванное давлением на днище цилиндра. Это напряжение можно считать постоянным по всем точкам поперечного сечения цилиндра.

На элемент AB действуют в плоскости чертежа две силы coставляющие между собой угол , и радиальная сила, равная

Эта сила направлена в сторону наружной поверхности. Уравновешиваясь, эти три силы составляют замкнутый треугольник abc (Рис.2).

Рис.2. Условия равновесия элемента кольца

Из него следует, что радиальная сила, изображаемая отрезком ab , связана с силой (отрезок са ) соотношением

пренебрегая малыми высшего порядка, получаем:

(1)

Условие равновесия дало только одно уравнение для нахождения двух неизвестных напряжений. Задача статически неопределима, и необходимо обратиться к рассмотрению деформаций. Деформация цилиндра будет заключаться в его удлинении и в радиальном, перемещении всех точек его поперечных сечений. Назовем радиальное перемещение точек внутренней поверхности рассматриваемого элемента через u (Рис.3). Точки наружной поверхности переместятся по радиусу на другую величину ; таким образом, толщина dr r одинаково), и сечение остается плоским

будет иметь место в точках внутренней поверхности цилиндра и всегда будет по абсолютной величине значительно больше внутреннего давления.

Таким образом, остаточные деформации появятся прежде всего у внутренней поверхности цилиндра, когда будет равно пределу текучести материала; борьба с их появлением путем увеличения наружного радиуса практически безнадежна, - с увеличением растут и числитель, и знаменатель формулы (11); поэтому разность главных напряжений хотя и убывает, но очень медленно. Однако момент появления пластических деформаций у внутренней поверхности цилиндра далеко не соответствует исчерпанию грузоподъемности конструкции; для правильной оценки прочности цилиндра необходимо перейти к расчету по допускаемым нагрузкам.

Рис.4. Динамика зоны текучести по толщине цилиндра

Полное исчерпание грузоподъемности произойдет тогда, когда кольцевая пластическая зона, распространяясь от внутренней поверхности цилиндра, дойдет до наружной; состояние разрушения наступит тогда, когда материал у наружной поверхности достигнет состояния, при котором произойдет разрыв. На фиг. 544 показано отношение внутреннего давления , при котором пластическая зона охватывает все сечение, к давлению, соответствующему началу пластических деформаций . Оказывается, что действительная грузоподъемность значительно выше получаемой при обычном методе расчета.

Упругая грузоподъемность толстостенных цилиндров может быть поднята путем создания начальных напряжений. Для этого необходимо изготовить цилиндр, составленный из двух цилиндров, вставленных один в другой; наружный диаметр внутреннего цилиндра делается несколько больше внутреннего диаметра наружного цилиндра; после одевания наружного цилиндра в нагретом состоянии на внутренний и его остывания по поверхности соприкасания возникнут реакция, сжимающие внутренний и растягивающие внешний цилиндры. Наличие этих начальных на Эта тема принадлежит разделу:

Введение и основные понятия. Метод сечений для определения внутренних усилий. Эпюры внутренних усилий при растяжении-сжатии и кручении

Метод сечений для определения внутренних усилий... Эпюры внутренних усилий при растяжении сжатии и кручении... Эпюры внутренних усилий при прямом изгибе...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Статически неопределимой называется система, внутренние усилия которой нельзя определить только из уравнений статики (равновесия). Статически неопределимые системы (СНС) отличаются от статически определимых рядом свойств:

1. Они надежнее, разрушение некоторых элементов не всегда приводит к разрушению всей системы.

2. Они выдерживают бо́льшую нагрузку.

3. У них деформации меньше.

4. Изменение температуры, смещение опор, неточность изготовления элементов вызывают дополнительные усилия.

5. Внутренние усилия зависят от физических и геометрических характеристик элементов.

У статически неопределимых систем есть так называемые «лишние» связи, число которых называется степенью статической неопределимости . Степень статической неопределимости n простой системы определяется из дискового аналога по следующей формуле:

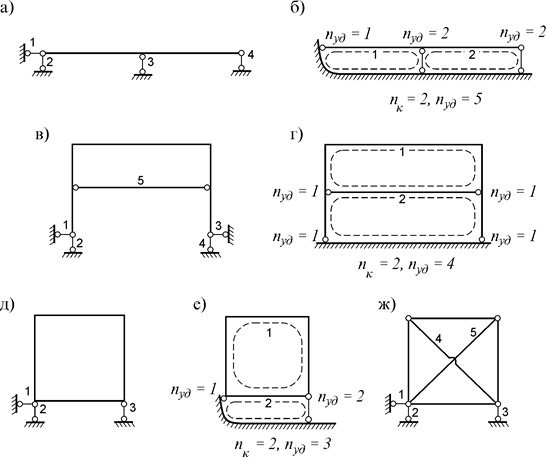
Например, степени статической неопределимости балки (рис. 7.1 а) и рамы (рис. 7.1 в) будут:

n=2·0+0+4–3·1=1 и n=2·0+1+4–3·1=2 .

Использование этой формулы при расчете сложных рам затруднительно. Поэтому можно применить другой подход, вводя два понятия: 1) замкнутый контур – замкнутая цепь из элементов и связей системы; 2) удалённая связь – связь замкнутого контура, исключенная из жесткого соединения элементов (см. рис. 7.1 б, г, е).

Степень статической неопределимости сплошного замкнутого контура равняется трем. Поэтому степень статической неопределимости системы из n к замкнутых контуров, из которых удалены n уд связей, будет

n=3n к – n уд.

При использовании этой формулы для балки (рис. 7.1 а) и рам (рис. 7.1 в, д) в этих системах необходимо определить общее число замкнутых контуров n к и удаленных связей n уд (рис. 7.4 б, г, е). Тогда

− для балки: n=3×2–5=1 ;

− для рам: n=3×2–4=2 , n=3×2–4=2.

Степень статической неопределимости фермы определяется по формуле

n= n С + n –2n У .

Например, для фермы (рис. 7.1 ж): n=6+3–2×4=1 .

Выбор основной системы

Расчет статически неопределимой системы начинается с превращения ее в статически определимую. Для этого необходимо исключить лишние связи и заменить их реакции неизвестными силами. Полученная система называется основной системой (ОС).

Например, у балки (рис. 7.2 а), которую далее будем называть заданной системой (ЗС), степень статической неопределимости n=1 . Если исключить лишнюю связь (правую опору) и обозначить неизвестную реакцию через X , получим ее ОС (рис. 7.2 б).

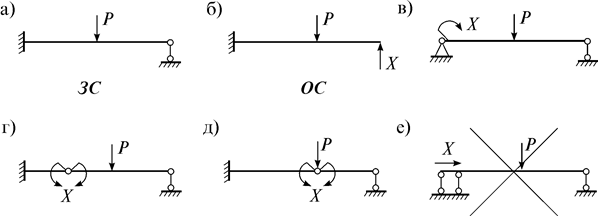
Способов исключения лишних связей очень много (теоретически – бесконечное число). Например, лишнюю связь можно исключать как на рис. 7.2 в-е. Однако одна из этих схем (рис. 7.2 е) геометрически изменяема и для дальнейшего расчета непригодна. Все остальные схемы могут быть приняты за основную систему.

Если воспользоваться известным теоретическим положением о том, что в линейно-упругих системах внешняя нагрузка распределяется единственным образом, то результаты расчетов по различным ОС должны быть одинаковыми. Однако объем вычислений в разных ОС может быть разным. Поэтому из многих вариантов ОС нужно выбирать наиболее оптимальную. Например, в нашем примере первый вариант ОС (рис. 7.2 б) предпочтительнее остальных, т.к. в ней эпюры строятся легче.

Итак, основная система должна быть:

1) обязательно геометрически неизменяемой;

2) простой для расчета;

3) учитывать особенности сооружения и действующей нагрузки.

Сущность метода сил

В рассматриваемом методе расчета статически неопределимых систем за основные неизвестные принимаются силы (внутренние усилия). Поэтому он и называется методом сил .

Изучим метод сил на примере предыдущей балки (рис. 7.2 а).

Потребуем, чтобы ее ЗС (рис. 7.2 а) и ОС (рис. 7.2 б) были эквивалентными. Для этого перемещение в направлении исключенной связи должно равняться нулю:

По принципу суперпозиции, это перемещение равно сумме перемещения D X (рис. 7.3 а) от неизвестной реакции X и перемещения D P (рис. 7.3 б) от заданной силы P . Поэтому

D=D X +D P =0.

Это уравнение, учитывающее геометрические особенности системы, называется уравнениемсовместности деформаций .