Напряжения растяжения и изгиба в стержне от действия внешних сил

Предположим, что температура тела во время работы не изменяется. Тогда, полагая в соотношении получим

Учитывая равенства найдем общую формулу для нормальных напряжений в стержне при действии внешних силовых факторов;

где - жесткость при растяжении; жесткости при изгибе.

Для стержня с постоянным модулем упругости (основной расчетный случай)

где - площадь поперечного сечения;

Моменты инерции сечения относительно осей х и у соответственно.

Первый член в правой части равенства (18) выражает напряжения от растяжения или сжатия, два последующих члена - напряжения изгиба.

Замечания. 1. Формула (18) является одной из основных во всем сопротивления материалов. Она показывает, что для анализа напряжений за начало координат надо принять центр тяжести сечения и к этой точке сечения (точнее, к системе координат) привести внешние силы. Нормальное усилие, действующее в центре тяжести, вызывает напряжения растяжения или сжатия, одинаковые во всех точках сечения.

Напряжения изгиба зависят от величины изгибающих моментов, геометрических характеристик сечения (моментов инерции) и координат точки.

2. Нормальные напряжения от внешних силовых факторов не зависят от абсолютной величины модуля упругости материала, а только от его распределения в точках сечения. Из равенства (17) следует, что при изменении модуля упругости во всех точках сечения одновременно в к раз напряжения остаются прежними.

Если модуль упругости одинаков во всех точках сечения (формула (18)), то напряжения в стержне не зависят от Е. В стальном или дюралевом стержне при одинаковых геометрических размерах и действующих нагрузках напряжения не различаются. Упругие перемещения стержней будут, разумеется, разными. Для закона распределения напряжений (формула (18)) решающим было предположение об упругости материала. Подобный результат имеет общее значение в задачах теории упругости.

3. Формулы (17) и (18) применимы и для стержней переменного сечения, когда упруго-геометрические характеристики сечения изменяются по длине стержня достаточно плавно.

Пример и некоторые дополнительные понятия.

Определим напряжения при изгибе стержня прямоугольного сечения под действием сосредоточенной силы Р (рис. 8.7).

Рис. 8.7. Изгиб стержня прямоугольного сечения: а - стержень; б - поперечное сечение стержня

Рассмотрим сечение на расстоянии z от заделки. Начало координат поместим в центре тяжести сечения.

Изгибающий момент возрастает по мере удаления от точки приложения силы. Напряжения изгиба определим по формуле (18), считая модуль упругости материала стержня постоянным.

Учитывая, что осевое усилие N и изгибающий момент отсутствуют, получим

Остается определить момент инерции поперечного сечения:

и окончательно

Опасным будет сечение, в котором действует наибольшее напряжение. Если стержень призматический, то опасным будет сечение, где изгибающий момент наибольший. В рассматриваемом примере оно расположено в заделке стержня.

Как следует из равенства (20), напряжения изгиба распределяются линейно по высоте сечения. В точках сечения, лежащих на линии у = 0, напряжения изгиба отсутствуют. Линия, в точках которой напряжения изгиба отсутствуют, называется нейтральной линией сечения. В рассматриваемом примере нейтральной линией является ось х. По мере удаления от нейтральной линии напряжения изгиба возрастают. В опасном сечении (z = 0) точки с наибольшими напряжениями изгиба называются опасными точками. Максимальное напряжение изгиба будет при

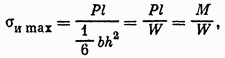
где М - действующий в рассматриваемом сечении изгибающий момент.

Величина - называется моментом сопротивления сечения изгибу. В точке ) напряжение изгиба будет таким же по величине, но противоположным по знаку:

Расчетные формулы (17) и (18) для нормальных напряжений в стержне по своей структуре достаточно просты, затруднения могут возникнуть при определении главных осей и упруго-геометрических характеристик сеченияг что будет разобрано в следующем разделе, а сейчас рассмотрим вкратце расчет температурных напряжений.

Коэффициент в формуле (15.45) берется потому, что сила

меняется от нуля до своего конечного значения.

Приравнивая значение кинетической єнергии (15.44) величине потенциальной энергии деформации (15.45), получим:

. (15.46)

Выражая динамическое перемещение

и подставляя в формулу (15.46), имеем:

или после некоторых преобразований

. (15.47)

Уравнение (15.47) имеет два корня:

. (15.48)

Из двух корней (15.48) оставляем положительный:

. (15.49)

Таким образом, окончательно динамический коэффициент при ударе принимает вид (15.49).

Полученное решение является приближенным, так как при выводе формулы (15.49) не был учтен целый ряд факторов, а именно: удар считался неупругим, в реальной системе он является частично упругим. Не были учтены местные деформации в точке, по которой наносится удар. Учет местных деформаций может оказать существенное влияние на окончательный результат. Из-за сделанных отступлений от реальных условий формула (15.49) дает завышенное значение динамического коэффициента.

Если масса на балке отсутствует, т.е.

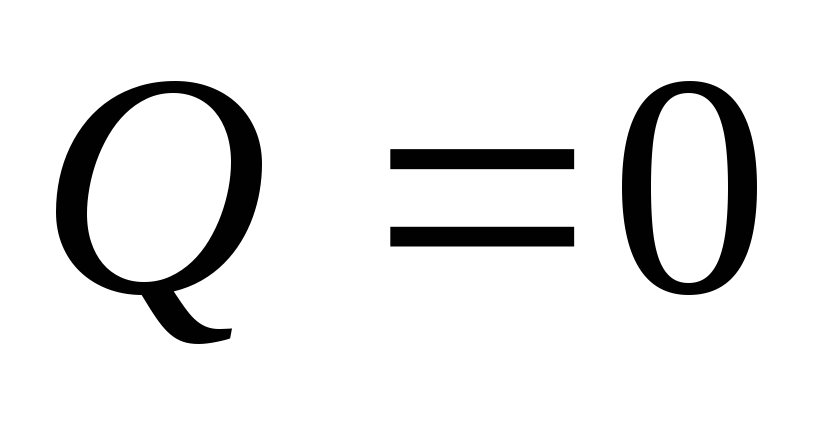, а телопадает на невесомую балку, то динамический коэффициент будет равен:

. (15.50)

Из формулы (15.50) следует, чем больше статическое удлинение

, тем меньше динамический коэффициент. Чем больше жесткость системы, тем больше величина ударной силы. Уменьшить силу удара можно, увеличив

. При продольном ударе, чем больше длина стержня и меньше его жесткость, тем меньше динамический коэффициент, а, следовательно, меньше динамическая сила и динамические напряжения. Этим можно объяснить то, что при буксировке тяжелых барж канаты, соединяющие буксирный катер с баржей, имеют большую длину. Короткие канаты при случайцном ударе, возникающем вследствие различных причин, не выдерживают динамичесой нагрузки и разрываются.

Этим же объясняется установка демпфирующих пружин и рессор, деформация которых сильно увеличивает статическое перемещение, и в результате уменьшается динамический коэффициент и динамические напряжения.

Величину динамического коэффициента при падении груза на невесомую балку можно выразить через скорость падения груза в момент подлета к балке. Для этого необходимо вместо величины

подставить величину, так как скорость падения груза в момент, предшествующий удару, связана с высотой падения равенством

. Следовательно:

. (15.51)

Когда высота падения равна нулю, динамический коэффициент равен двум. Такое загружение называется внезапным. Физически эту задачу можно представить так: если на нити подвесить груз, укрепив его над балкой таким образом, чтобы он касался верха балки, но не давил на нее, а передавался целиком на нить, и если при этом нить мгновенно рассечь, то груз всей своей величиной передастся на балку. Напряжения и прогибы в этом случае будут в два раза больше, чем при статическом нагружении, при котром предполагается постепенное нарастание величины нагрузки от нуля до конечного значения.

Если высота падения значительно превыщает статичесий прогиб

, то единицей по сравнению со вторым членом, стоящим под корнем, можно пренебречь. Тогда

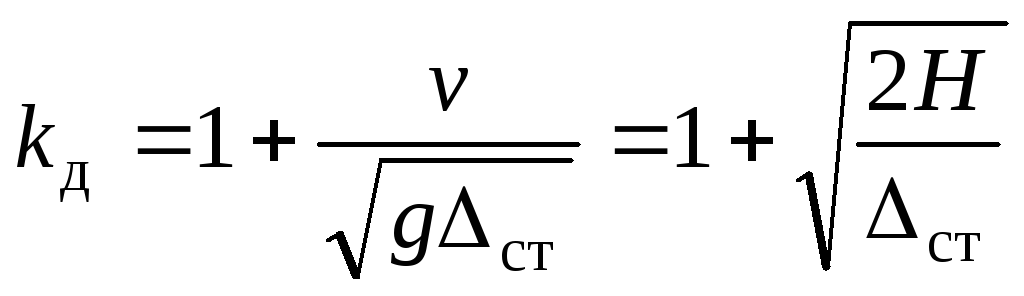. (15.52)

15.6.Учет собственного веса при ударе

Если груз падает на балку, обладающую значительным весом, которым нельзы пренебречь (Рис.15.11,а), то решение сильно усложняется. В этом случае применяют приближенное решение, которое сводится к замене реальной балки системой с одной степенью свободы. Распределенная по длине балки масса заменяется приведенной массой, сосредоточенной в месте удара (Рис.15.11,б).

Буквой

обозначен приведенный вес. Приведенным он называется потому, что прогиб от равнодействующей сосредоточенной силы, заменяющей распределенную нагрузку, будет больше. Поэтому весь вес посредине балки прикладывать нельзя. Величину приведенного веса найдем, используя динамическую эквивалентность двух систем: исходной системы (Рис.15.11,а) и динамически эквивалентной (Рис.15.11,б).

Две системы называются динамически эквивалентными, если их кинетические энергии одинаковы. Найдем значения коэффициентов приведения для некоторых частных случаев.

1. Продольный удар. Определим величину коэффициента для случая продольного удара по стержню постоянного сечения, заделанного одним концом (Рис.15.12,а). Вес стержня равномерно распределен по длине стержня в виде интенсивности распределенной нагрузки. Стержень подвергается удару грузом, который в начальный момент времени занимает верхнее положение в месте заделки.

Поместим начало координат в жесткой заделке, ось направим вниз. Выделим на расстоянииот начала координат бесконечно малый элемент длиной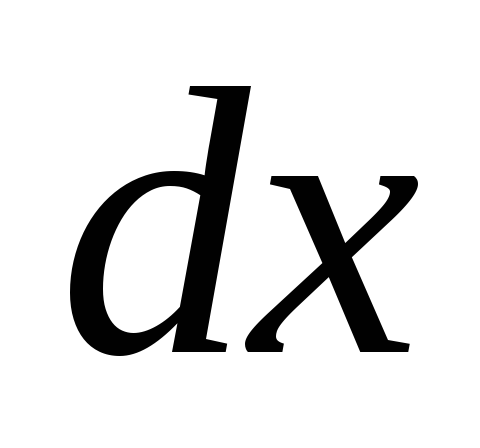

. Масса этого элемента

. Предположим, что скорость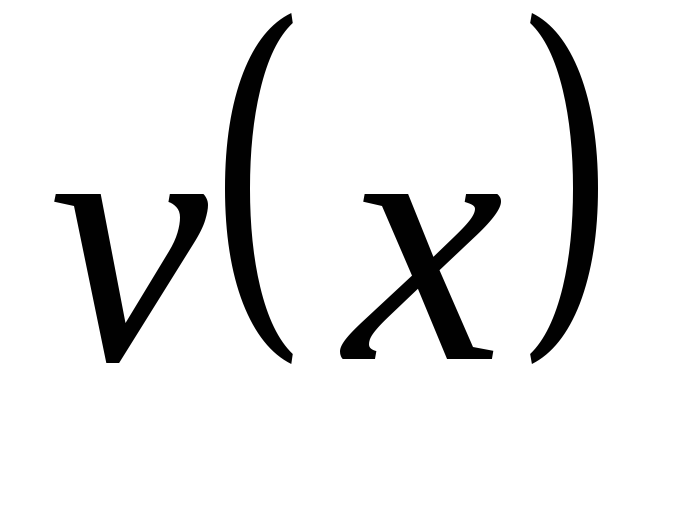

падения грузапропорциональна перемещению рассматриваемого сечения, которое в свою очередь пропорционально координате(Рис.15.12,б). Максимального значения

скорость падения груза достигает в нижней точке падения на нижнем конце стержня, где расположен упор. Тогда

.

Кинетическая энергия для исходной системы с распределенной массой имеет вид:

Кинетическая энергия динамически эквивалентной системы (Рис.15.11,в) равна:

.

Приравнивая найденные кинетические энергии (

) на основании принципа динамической эквивалентности двух систем, получим:

.

Откуда: .

2. Поперечный удар. Рассмотрим балку постоянного сечения, шарнирно закрепленную на двух опорах. Масса балки распределена равномерно по ее длине, интенсивность распределенной нагрузки составляет . Для определения кинетической энергии системы предположим, что скорость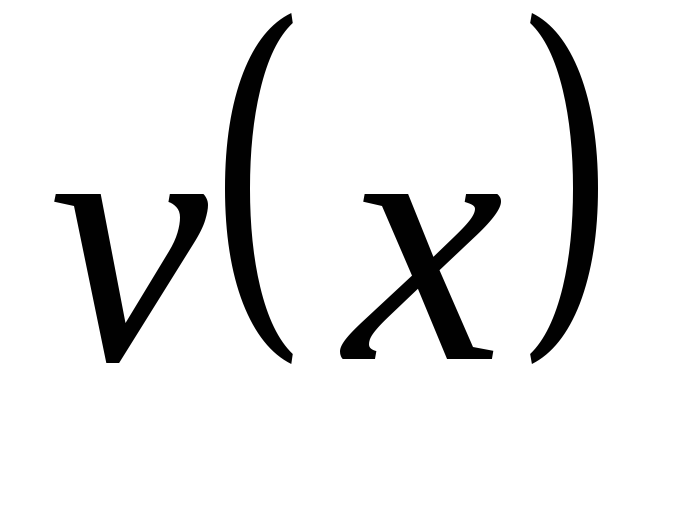

элемента балки, отстоящего от левой опоры на расстоянии(Рис.15.13,а) пропорциональна перемещению этого сечения

от статической нагрузки, приложенной в виде силыв точке удара. Это условие пропорциональности можно выразить следующим равенством:

.

Здесь

и

 соответственно скорость и прогиб в середине пролета.

Приняв, что точка удара расположена в середине балки (Рис.15.13,б), получим следующее уравнение прогибов:

.

Следовательно,

;

.

Кинетическую энергию найдем из равенства:

.

Определим теперь кинетическую энергию для балки, у которой посредине пролета прикреплена приведенная масса. Считая, что скорость движения этой массы будет равна

, получим:

.

Приравнивая полученные кинетические энергии (

) на основании принципа динамической эквивалентности двух систем, получаем значение коэффициента:

.

Для случая, изображенного ра рис.15.14, коэффициент

.

Для других случаев нагружения балок можно брать значение для коэффициента приведения массы в соответсвующих справочниках по сопротивлению материалов.

Таким образом, динамический коэффициент при ударе с учетом распределенной массы приобретает вид:

. (15.53)

Динамический коэффициент при ударе можно также выразить через значения кинетической энергии ударяющего тела 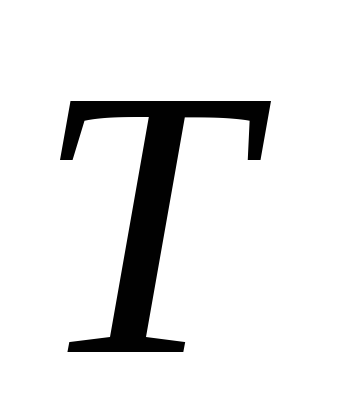и потенциальную энергию ударяемого тела при статической деформации

:

. (15.54)

При продольном ударе силой потенциальная энергия стержня имеет вид:

. (15.55)

Для вычисления динамического коэффициента при этом может быть выбрано одно из выражений:

При поперечном ударе нагрузки величина статической деформации

, представляющей собой статический прогиб балки в месте удара, зависит от схемы нагоужения и условий опирания балки.

Так, например, для балки пролетом , шарнирно закрепленной по концам и испытывающей посредине пролета удар от падающего с высоты

груза, получаем:

;

;

.

Динамический коэффициент при этом принимает вид:

.

Для консоли, испытывающей удар от груза , падающего на свободный конец консоли:

;

;

.

Динамический коэффициент для консольной балки имеет вид:

.

Максимальные динамические напряжения для балки на двух опорах принимают вид:

.

Рассмотрим несколько примеров расчета конструкций, испытывающих удар.

Пример 15.12. Определить величину наибольшего нормального напряжения в стальном ступенчатом стержне (Рис.15.15), подвергающемся действию удара при падении груза

кН с высоты

мм. Площадь поперечного сечения стержня

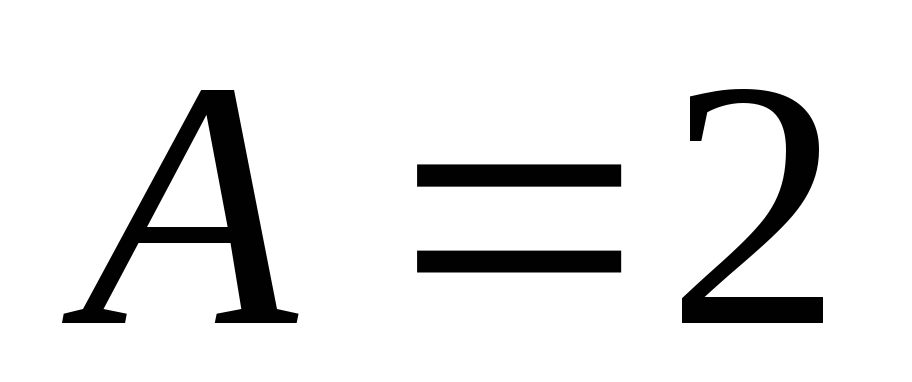см 2 , длина стержня

м. Какое наибольшее напряжение возникнет в стержне, если на кольцевой выступ В для смягчения удара поместить цилиндрическую винтовую пружину, которая при действии статической нагрузки, равной 10Н, сжимается на

мм?

Вычисляем коэффициент динамичности:

.

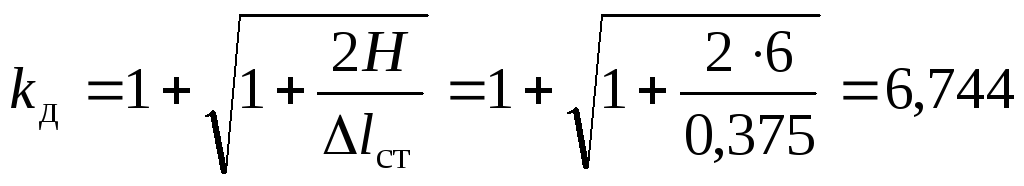3. Определяем наибольшие динамические нормальные напряжения в стержне при осутствии пружины:

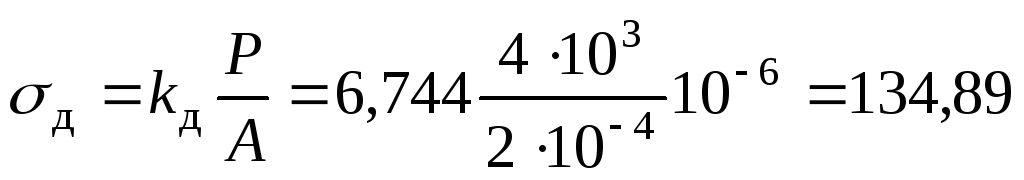МПа.

4. Определяем статическое перемещение с учетом осадки пружины. Жесткость пружины

мм/Н. Осадка пружинымм.

Вычисляем динамический коэффициент:

.

6. Определяем наибольшие динамические напряжения в стержне при наличии пружины:

МПа.

Пример 15.13. Стержень, имеющий длину

м и площадь поперечного сечения

см 2 , подвергается продольному растягивающему удару при падении груза

кН. Кинетическая энергия груза к моменту соударения равна

Нм. Найти напряжение в стержне при ударе в предположении, что он изготовлен из стали.

1. Вычисляем потенциальную энергию, накапливаемую в стержне, при статическом приложении силы :

Нм.

2. Определяем динамический коэффициент по формуле:

.

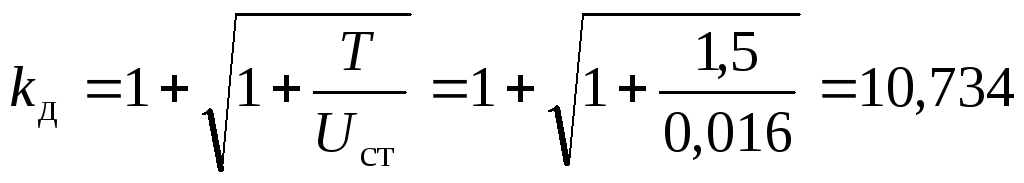3. Находим динамические напряжения в стержне:

МПа.

Пример 15.14. На шарнирно опертый по концам деревянный брус прямоугольного поперечного сеченния

см 2 посредине пролета

м с высоты

см падает груз

кН. Определить наибольшее нормальное напряжение и наибольший прогиб бруса при изгибающем моменте в плоскости наибольшей жесткости. Модуль упругости дерева

МПа.

Определяем стрелу прогиба при статическом приложении нагрузки:

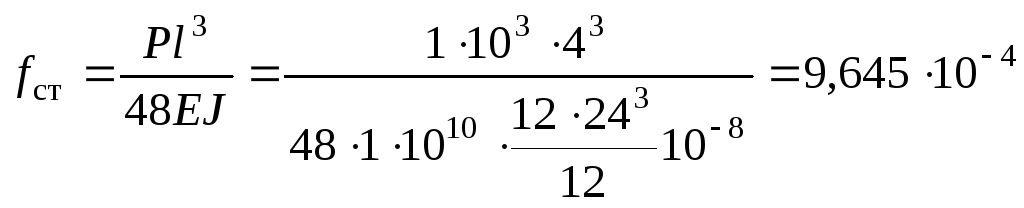м.

2. Находим динамический коэффициент:

.

3. Определяем динамические напряжения в брусе:

МПа.

4. Находим максимальный динамический прогиб в плоскости наибольшей гибкости:

м

мм.

Пример 15.15. Двутавровая балка №24 длиной

м опирается на шарнирные опоры. Груз

кН падает посредине пролета со скоростью

м/сек к моменту удара (Рис.15.16,а). Определить наибольшее нормальное напряжение и наибольший прогиб в результате удара, предполагая, что: а) опоры балки абсолютно жесткие; б) опоры балки представляют упругие конструкции; смещение каждой из них на единицу приложенной к ней нагрузки равно

м/Н; в) опоры балки абсолютно жесткие, но посредине пролета лежит груз

кН. Массой балки во всех случаях пренебречь. Момент инерции двутавра №24

см 4 , момент сопротивления

см 3 .

Опоры абсолютно жесткие. Определяем стрелу прогиба:

Находим коэффициент динамичности:

Определяем наибольшие динамические напряжения в балке и максимальный прогиб:

м

мм.

2. Опоры балки – упругие конструкции. Определяем осадку пружины на опоре от статического приложения нагрузки:

Находим перемещение сечения посредине балки с учетом осадки пружин:

Определяем коэффициент динамичности:

Вычисляем максимальные динамические напряжения в балке и динамическую стрелу прогиба:

м

мм.

3. Опоры жесткие, груз падает на груз, расположенный посредине балки. Определяем динамический коэффициент:

Находим наибольшие динамические напряжения и динамическую стрелу прогиба:

м

мм.

Пример 15.16. Льдина, плывущая со скоростью

м/с, ударяется о деревянную сваю круглого поперечного сечения (Рис.15.17). Определить наибольшее нормальное напряжение и наибольший прогиб сваи при ударе, если модуль упругости дерева

МПа. Сваю в нижнем сечении считать жестко защемленной.

1. В момент удара свая испытывает действие динамической силы

со стороны льдины. Найдем эту силу. Кинетическая энергия удара равняется потенциальной энергии деформации, накапливаемой в свае от действия динамической силы

:

.

Потенциальную энергию найдем, выражая ее через динамическую силу:

.

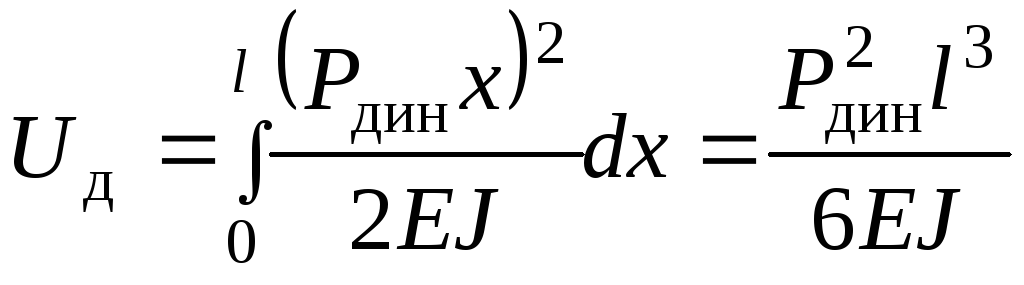Приравнивая кинетическую и потенциальную энергии, получаем:

,

Определяем наибольший прогиб сваи:

м

см.

Вычисляем наибольшее напряжение в свае:

МПа.

Пример 15.17. Деревянная балка круглого поперечного сечения и длиной

м, шарнирно оперта на концах, посредине пролета испытывает удар телом, движущимся горизонтально. Тело имеет в начальный момент удара кинетическую энергию

Нм. Определить диаметрпоперечного сечения балки таким образом, чтобы наибольшее нормальное напряжение в ней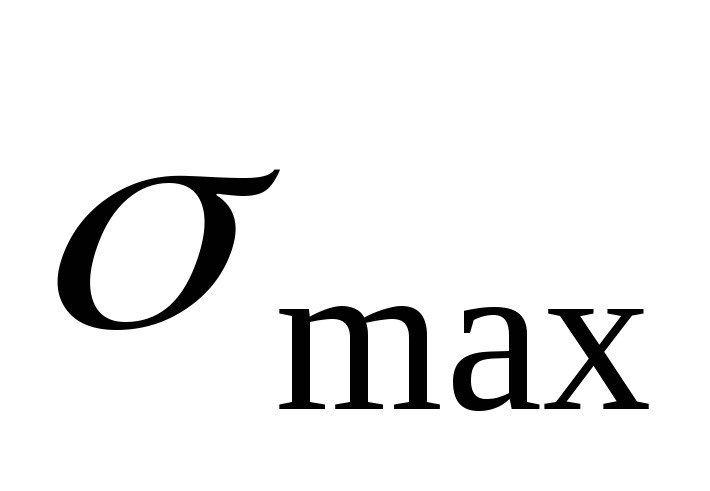

не превышало 10МПа, а максимальный прогиббыл не больше 1 см.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ПОЛТАВСКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Ю. Кондратюка

ТЕМА: Внутренние силы и напряжения, возникающие в поперечных сечениях бруса при растяжении и сжатии

Выполнила: студентка V курса

Группа ЕФ145

Михайлова Виктория

Полтава 2009

Под растяжением, понимается такой вид нагружения, при котором в поперечных сечениях бруса (стержня) возникают только нормальные силы, а все прочие внутренние силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 15. Во всех случаях, однако, система внешних сил образует равнодействующую Р, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня расчетная схема в рассматриваемых случаях оказывается единой. Она показана на рис. 15, г.

Если воспользоваться методом сечений, то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N, равные силе Р (рис. 16),

Сжатие отличается от растяжения, формально говоря, только знаком силы N. При растяжении нормальная сила N направлена от сечения, а при сжатии - к сечению. Таким образом, при анализе внутренних сил сохраняется единство подхода к вопросам растяжения и сжатия. Вместе с тем между этими двумя типами нагружения могут обнаружиться и качественные различия, как, например, при изучении процессов разрушения материалов или при исследовании поведения длинных и тонких стержней, для которых сжатие сопровождается, как правило, изгибом.

Рассмотрим напряжения, возникающие в поперечном сечении растянутого стержня. Нормальная сила N является равнодействующей внутренних сил в сечении (рис. 17). Естественно предположить, что для однородного стержня внутренние силы распределены по сечению равномерно. Тогда нормальное напряжение для всех точек сечения будет одним и тем же:

где Р - площадь поперечного сечения.

Понятно, что высказанное предположение о равномерном распределении внутренних сил в поперечном сечении справедливо лишь постольку, поскольку из рассмотрения исключаются особенности конкретно взятого стержня в связи с условиями его закрепления на концах. Здесь руководствуются правилом, которое принято называть принципом Сен-Венана, по имени известного французского ученого прошлого века. Принцип Сен-Венана является общим, но применительно к стержням он может быть сформулирован следующим образом. Особенности приложения внешних сил к растянутому стержню проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня. Это значит, исключение составляют тонкостенные стержни (см, гл. XI).

Что при изучении растянутого стержня достаточно принимать во внимание только равнодействующую внешних сил Р, не интересуясь особенностями приложения нагрузки. Для этого надо исключить из рассмотрения часть стержня, расположенную в зоне приложения внеших сил. На рис. 15 это как раз и показано. Отбрасывая части стержня, примыкающие к его концам, получаем единую расчетную схему (рис. 15, г), независимо от способа приложения внешних сил.

Приведенные рассуждения могут быть отнесены также и к особым участкам стержня, содержащим резкое изменение геометрических форм. Например, для ступенчатого бруса, показанного на рис. 18, следует исключить из рассмотрения зону скачкообразного перехода от одного диаметра к другому и зоны, примыкающие к отверстиям. Во всех остальных участках напряжения в поперечных сечениях будут распределены равномерно и определяются по формуле (1.1).

Для однородного, растянутого, нагруженного по концам стержня напряжения остаются постоянными как по сечению, так и по длине, т. е. сохраняются неизменными для всех точек объема, занимаемого телом. Такое напряженное состояние называется однородным. При однородном напряженном состоянии все точки тела находятся в одинаковых условиях. Понятие однородного напряженного состояния тесно связано с понятием сплошной среды. Ясно, что распределение внутренних сил в реальных условиях не может быть равномерным из-за неоднородности кристаллических зерен металла и молекулярного строения вещества. Поэтому, когда говорят о равномерном распределении внутренних сил по сечению, имеют в виду распределение без микроскопической детализации в пределах площадок, существенно превышающих размеры сечений кристаллических зерен. Сделанная оговорка относится не только к растяжению и сжатию, но и вообще ко всем другим видам нагружения, которые будут рассмотрены в дальнейшем.

При растяжении, однако, не всегда возникает однородное напряженное состояние. Так, например, у стержня с переменной площадью поперечного сечения (рис. 19, а) напряжения меняются по длине и напряженное состояние не однородно. То же самое имеет место и для стержня, нагруженного собственным весом (рис. 19, б).

Размеры растянутого стержня меняются в зависимости от величины приложенных сил. Если до нагружения стержня его длина была равна /, то после нагружения она станет равной(рис. 20).

Величину А называют абсолютным удлинением стержня.

Будем считать, что абсолютное удлинение и деформации связаны только с напряжениями, возникающими в стержне. В действительности имеются и другие факторы, влияющие на величину деформаций. Так, например, деформации зависят от температуры и от времени действия нагрузки. Величина неупругих деформаций зависит от «истории» нагружения, т. е. от порядка возрастания и убывания внешних сил. Пока, однако, этих вопросов мы касаться не будем.

Поскольку у нагруженного стержня (рис. 20) напряженное состояние является однородным и все участки растянутого стержня находятся в одинаковых условиях, деформация е по оси стержня остается одной и той же, равной своему среднему значению по длине l:

Эта величина называется относительным удлинением стержня.

Если бы в стержне (рис. 20) возникало неоднородное напряженное состояние, деформация в сечении А определялась бы путем предельного перехода к малому участку длиной dz и тогда

Заметим, что вследствие равномерного распределения напряжений по сечению удлинения для всех элементарных отрезков аЬ (рис. 20), взятых на участке, оказываются одинаковыми. Следовательно, если концы отрезков до нагружения образуют плоскость, ТО и после нагружения стержня они образуют плоскость, но смещенную вдоль оси стержня. Это положение может быть взято в основу толкования механизма растяжения и сжатия и трактуется как гипотеза плоских сечений (гипотеза Бернулли). Если эту гипотезу принять как основную, то тогда из нее, уже как следствие, вытекает высказанное ранее предположение о равномерности распределения напряжений в поперечном сечении.

В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность междунапряжениями и деформациями:

Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода. Модуль упругости является физической, константой материала и определяется путем эксперимента. Величина Е измеряется в тех же единицах, что и а, т. е. в кГ/см2. Для наиболее часто применяемых материалов модуль упругости имеет следующие значения в кГ/см2:

Закон Гука является приближенным. Для некоторых материалов, таких, как, например, сталь, он соблюдается с большой степенью точности в широких пределах изменения напряжений. В некоторых же случаях наблюдаются заметные отклонения от закона Гука. Например, для чугуна и некоторых строительных материалов даже при малых напряжениях закон Гука может быть принят только в грубом приближении. В тех случаях, когда закон Гука явно не соблюдается, деформацию задают в виде некоторой нелинейной функции от напряжения

с таким расчетом, чтобы эта функция отвечала кривой, полученной из испытания материала.

Вернемся к выражению (1.4) и заменим в нем о на , а е на Тогда получим

Абсолютное удлинение стержня на длине l будет равно

В том случае, когда стержень нагружен только по концам, нормальная сила N = Р не зависит от г. Если, кроме того, стержень имеет постоянные размеры поперечного сечения Р, то из выражения (1.5) получаем

При решении многих практических задач возникает необходимость наряду с удлинениями, обусловленными напряжением учитывать также удлинения, связанные с температурным воздействием. В этом случае пользуются способом наложения и деформацию е рассматривают как сумму силовой деформации и чисто температурной деформации:

где а - коэффициент температурного расширения материала.

Для однородного стержня, нагруженного по концам и равномерно нагретого, получаем, очевидно,

Таким образом, силовая и температурная деформации рассматриваются как независимые. Основанием к этому служит экспериментально установленный факт, что модуль упругости Е при умеренном нагреве слабо меняется с температурой, точно так же как и величина а практически не зависит от напряженияДля стали это имеет место до температуры порядка 300-400° С. При более высоких температурах необходимо учитывать зависимость

Рассмотрим примеры определения напряжений и перемещений в некоторых простейших случаях растяжения и сжатия.

Пример 1.1. Требуется выявить закон изменения нормальных сил, напряжений и перемещений по длине ступенчатого стержня, нагруженного на конце силой Р (рис. 21, а), определить числовые значения наибольшего напряжения и наибольшего перемещения, еслиМатериал - сталь,

Поскольку сила Р велика, собственный вес стержня не имеет значения.

Из условий равновесия любой отсеченной части стержня вытекает, что нормальная сила N в каждом сечении стержня численно равна внешней силе Р. Построим график изменения силы N вдоль оси стержня. Графики подобного рода называются в сопротивлении материалов эпюрами. Они Дают наглядное представление о законах изменения различных исследуемых величин. В данном случае эпюра нормальной силы представлена на рис. 21, б прямоугольником, посколькуНа рисунке эпюра N заштрихована линиями, которые проведены в направлении откладываемой на графике величины N. В данном случае значение силы N откладывается вверх, следовательно, штриховка проведена Вертикально.

Для того чтобы получить эпюру напряжений 0, надо ординаты эпюры N изменить обратно пропорционально величине Р (рис. 21, е). Большее значение о равно

Определим, на какую величину и (см) переместится каждое сечение стержня по направлению силы Р. Перемещениесечения равно удлинению отрезка

Длиной Следовательно, согласно формуле (1.6)

Таким образом, на участке изменения перемещение и пропорционально г (рис. 21, г). На втором участке стержня перемещение равно

Зависимостьтакже будет линейной. Наибольшее перемещение имеет торцевое сечение стержня

Пример 1.2. Построить эпюры нормальных сил, напряжений и перемещений для свободно подвешенного цилиндрического стержня, нагруженного силами собственного веса (рис. 22). Длина стержня площадь поперечного сечения Р, удельный вес материалаНормальная сила в сеченииравна весу нижележащей части стержня: Следовательно, нормальная сила пропорциональнаЭпюра. А в данном случае штрихуется горизонтальными линиями, поскольку величины N откладываются в горизонтальном направлении. Напряжение в сечении равно (см. эпюру на рис. 22).

Перемещение и в сечении г равно удлинению верхнего участка стержня.По формуле (1.5). Таким образом, закон изменения и изображается квадратичной функцией Наибольшее перемещение имеет нижнее торцевое сечение

Пример1.3. Колонна (рис.23) нагружена силой Р Такими силами собственного веса. Требуется подобрать такой закон изменения площади поперечного сечения чтобы напряжения во всех сечениях были одинаковы и равныПостроить эпюры нормальных сил, напряжений и перемещений.

На расстоянии г от торца нормальная сжимающая сила N равна

По условию задачи

откуда

Дифференцируя обе часта этого равенства по г, получим Или

После интегрирования находим

Приследовательно,и тогда искомый закон изменения

площади Г принимает вид

Построение эпюр удобнее всего начинать с эпюры напряжения а, которое вдоль оси колонны по условию не меняется (рис. 23). Поскольку напряжение постоянно, то постоянным будет и относительное удлинение е. Поэтому перемещение и возрастает пропорционально расстоянию от основания колонны.

Нормальная сила в сечении равна

Эпюра Л показана на рис. 2.3.

Рассмотренная задача относится к числу часто встречающихся в сопротивлении материалов задач на отыскание условий равнопрочное™. Если напряжение в некотором теле (в данном случае в колонне) будет постоянно для всех точек объёма, такую конструкцию называют равнопрочной. В подобных конструкциях материал используется наиболее эффективно.

Пример 1.4. Кронштейн АВС нагружен на конце силой Р (рис. 24). Требуется подобрать поперечное сечение стержней А В и ВС с таким расчетом, чтобы возникающие в них напряжения имели одинаковую заданную величину а. При этом уголдолжен быть выбран из условия минимального веса конструкции при заданном вылете кронштейна

Из условий равновесия узла В (рис. 24) находим нормальные силы в стержнях:

Вес конструкции кронштейна пропорционален объему

Подставляя длины и площади стержней, находим

Величина V имеет минимум при

Использованная литература

1. Феодосьев В. И. Сопротивление материалов. – 8-е изд., стереотип – М.:

Наука. Главная редакция физико –математической литературы, 1979. – 560 с.

Действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение. Еще одно свойство пары сил, которое является основой для сложения пар: − не нарушая состояния тела, можно как угодно изменять модули сил и плечо пары, только бы момент пары оставался неизменным. По определению пары сил эквивалентны...

Касательных напряжений Задача 7 Для заданной схемы требуется: 1. Построить эпюры изгибающих моментов и поперечных сил; 2. Подобрать по ГОСТ двутавровое сечение балки, принимая расчетное сопротивление изгибу Rи = 160 МПа 3. Построить в опасном сечении эпюру нормальных напряжений 4. В сечении с наибольшей поперечной силой построить эпюру касательных напряжений. Рис. 1. Расчетная...

Характере деформирования Расчет конструкций и их элементов с учетом всего многообразия физико-механических свойств реальных материалов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому, отказываясь от принятой в теоретической механике модели абсолютно твердого тела, в сопротивлении материалов приходится вводить свою модель - модель идеализированного...