Для плоской системы сходящихся сил достаточно будет двух уравнений.

Геометрически условие равновесия означает, что силовой многоугольник будет замкнут, т. е. при построении силового многоугольника конец последнего вектора совпадает с началом первого вектора.

Аналитически для равновесия системы сходящихся сил необ­ходимо и достаточно, чтобы проекции всех сил системы на соот­ветствующие координаты оси равнялись нулю:

Если твердое тело под действием трех непараллельных сил, две из которых пересекаются, находится в равновесии, то ли­нии их действия пересекаются в одной точке .

Задача 1. На середину балки АВ действует сила (рис. 16). В точке А балка имеет шарнирно-неподвижную опору, а в точке В - шарнирно-подвижную. Определить линию действия реакции в точ­ке А .

Решение . Реакция шарнирно-неподвижной опоры пер­пендикулярна опорной поверх­ности и пересекается с линией действия силы Р в точке С . По теореме о трех непараллельных силах реакция опоры А должна пройти через эту точку:

.

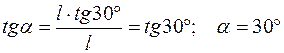Ответ . Реакция образует- угол 30° с осью балки АВ .

Задача 2. Два невесомых стержня, соединенные в точке С шарниром, удерживают груз Р = 50 Н , который нитью прикреплен к шарни­ру С . Найти усилия в стержнях АС и ВС , если = 60°.

Решение . Используя принцип освобождаемости от связей, заменяем действие стержней АС , ВС . и нити на шарнир С реакциями , , . Учтем, что Т= Р = 50 Н Реакции показаны на рис. 17. Считаем стерж­ни растянутыми и не делаем допол­нительный рисунок. Запишем урав­нения равновесия, учитывая, что конструкция находится в плоскости СХУ . Направления осей показаны на рисунке.

Находим из (2)

,

Отрицательное значение указывает, что стержень ВС сжат, а не растянут, как предполагалось.

Задача 3 . Груз весом G = 2 кН (рис. 1) удерживается краном, состоящим из двух невесомых стержней в шарнирах АВ и АС , прикрепленных к вертикальной стене и составляю­щих с ней углы α 1 = 60° и α 2 = 40°. В точке А подвешен блок, через который перекинут грузовой трос, идущий к блоку в точке D и составляющий со стеной угол α 3 = 60°.

Весом троса и блока, а также размерами блока можно пренебречь. Определить усилия в стержнях.

Решение . Рассмотрим находящийся в равновесии груз (рис. 2).

На него действуют две силы: сила тяжести G и сила натяжения троса N 1 . Поскольку система сил уравнове­шена, можно сделать очевидный вывод: сила натяжения троса направлена внутрь троса и по модулю равна весу груза N 1 = G .

Если для любого блока (рис. 3) пренебречь трением на его оси, то силы натяжения ветвей его троса одинаковы N 1 = N 2 (что легко видеть из уравнения моментов относи­тельно центра блока).

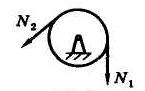
Рис. 1 Рис. 2 Рис. 3 Рис. 4

Теперь в качестве объекта равновесия можно рассмот­реть мысленно вырезанный узел в точке А (или, что то же самое, блок с прилежащей к нему частью троса). На этот узел будут действовать силы натяжения ветвей троса N 1 и N 2 и реакции R 1 и R 2 стержней АВ и АС (рис. 4).

Реакции опорных стержней направлены, как извест­но, вдоль этих стержней. Направим их внутрь стержней, считая изначально стержни растянутыми.

Составим теперь уравнения равновесия как уравне­ния проекций сил на оси (для системы сходящихся сил), учитывая, что силы R 1 , R 2 и N 2 составляют углы α 1 , α 2 и α 3 с осью у .

Отсюда, учитывая, что , получаем

Решая эту систему уравнений, находим R 1 = 0,611 кН , R 2 = –3,52 кН . Знак «минус» у величины реакции R 2 озна­чает, что она имеет направление, противоположное при­нятому, то есть стержень АС не растянут, а сжат.

Ответ: R 1 = 0,611 кН , R 2 = –3,52 кН .

Задача 4. На невесомую балку, закрепленную с помощью не­подвижного шарнира в точке А и троса в точке В , действу­ет сила F , модуль которой F = 5 кН (рис. 5). Учитывая указанные на рисунке геометриче­ские размеры, определить реакции опор балки.

Решение . Рассмотрим балку, воспользуемся принципом освобож­даемости от связей, отбросим их и введем соответствующие реакции. Реакция троса в точке В , как известно, направлена по тросу, а реакция шарнирно-неподвижной опоры имеет не­известное направление.

Рис. 6 Рис. 7

Однако в данном случае определить ее направление позволяет теорема о трех силах, согласно которой линии действия трех непараллельных сил, под действием кото­рых тело находится в равновесии, должны пересекаться в одной точке. В рассматриваемой схеме это будет точка О пересечения линий действия силы F и линии троса (рис. 6).

Таким образом, реакция в точке А проходит по линии АО под углом β , величину которого найдем из треугольни­ка: tg β = 1/3 и β = arctg 1/3.

Для определения величин реакций могут быть приме­нены три способа: графический, графоаналитический и аналитический.

1. Графический способ. Следует построить в масштабе замкнутый силовой многоугольник, начиная с известной силы F , а затем в произвольной последовательности ос­тальные силы R A и R B .

Например, можно провести из конца силы F линию действия реакции R B , а из ее начала - линию действия R A до их пересечения. Силы должны быть направлены в одну сторону по пути обхода контура (рис. 7).

Затем, измеряя отрезки и сравнивая их с масштабом, можно узнать величины неизвестных сил.

2. Графоаналитический способ. Здесь также строится силовой многоугольник, но только в виде геометрической схемы, рассматривая которую можно вычислить неизвестные стороны треугольника.

Для схемы (рис. 7) согласно теореме синусов получаем

где γ = 180°– 45° – (90° + β ) = 45°– β .

Из этих уравнений имеем

3. Аналитический способ. Здесь не требуется построе­ния силового многоугольника, необходима лишь расчет­ная схема с направлениями реакций (рис. 8). При этом не по линии действия направлять не­известные силы.

Выбирая координатные оси х и у , записываем уравнения рав­новесия в проекциях на эти оси:

Решая эту систему уравнений, получаем

Отрицательный знак у величины R A означает, что дей­ствительное направление этой реакции противоположно выбранному на схеме.

Ответ: R A = –7,9 кН ; R B = 10,6 кН .

Задача 5. Подвеска идеального блока О лебедки состоит из трех невесомых стержней в шарнирах: двух горизонтальных АО и ВО , составляющих углы 45° с перпендикуляром к стене DO , и стержня СО , составляющего угол 60° с вертикальной линией стены DE (рис. 9).

Через блок перекинут трос, на од­ном конце которого подвешен непо­движный груз весом G = 10 кН . Дру­гой конец, уходящий на лебедку, в точке Е стены составляет угол 30° с вертикалью DE . Определить усилия в стержнях подвески.

Решение . В качестве объекта, равновесие которого следует рассмот­реть, выберем блок вместе с прилега­ющей к нему частью троса (узел в точке О ).

При условии, что размерами его можно пренебречь, действующие на него силы представляют собой си­стему сходящихся сил. Учитывая, что реакции опорных стержней на­правлены по линиям этих стержней, а силы натяжения - по тросу, полу­чаем расчетную схему (рис. 10).

Здесь G 1 = G - сила натяжения ветви троса, идущей к лебедке в точке Е ; направления реакций стержней выбраны в предпо­ложении, что стержни АО и ВО растянуты, а стержень СО - сжат.

Для удобства геометрического рассмотрения начало координат взято в точке D, ось х направлена по линии АВ , ось у - по DO , ось z - по DE .

Записываем теперь условие уравновешенности систе­мы сходящихся сил.

в проекциях на декартовы оси:

х : R A sin 45° – R B sin 45° = 0;

у : – R A cos 45° – R B cos 45° + R С sin 60° – G sin 30° = 0;

z : R С cos60 о – G 1 cos30° – G = 0.

Решая эту систему, находим значения усилий в стерж­нях подвески:

R С = 37,3 кН ; R A = R B = 19,3 кН .

Все усилия получились положительными, значит их направления были изначально взяты правильно.

Можно отметить при этом, что усилия в стержнях под­вески оказались значительно большими, чем вес удержи­ваемого ими груза, и существенно зависят от геометриче­ских параметров (углов) самой конструкции подвески.

Ответ: R С = 37,3 кН ; R A = R B = 19,3 кН .

Влияние способов закрепления концов стержня

На рис. 8.3 показаны формы потери устойчивости стержней длиной с различными случаями закрепления концов. Случай б) нами рассмотрен при выводе формулы Эйлера. Этот случай называют основным случаем закрепления .

Для других случаев закрепления можно повторить все выкладки, изменяя в каждом случае только граничные условия и получить соответствующие значения . Однако можно пойти другим путем.

Рис.8.3

Сравнивая рис. а) и б) видим, что изогнутая ось стержня, защемленного одним концом, находится в тех же условиях, что и верхняя часть стержня длиной с шарнирными концами. Следовательно, для стойки длиной с одним защемленным концом будет та же, что для стойки длиной с шарнирными концами. Поэтому, подставляя вместо в формулу Эйлера найдем:

– Эйлерова сила для стержня с

одним защемленным концом.

На рис. г) показана потеря устойчивости стержня с двумя защемленными концами. Видно, что она симметрична относительно середины стержня; точки перегиба изогнутой оси (в которых, как известно, изгибающие моменты равны нулю) расположены на четвертях длины стержня. Следовательно, здесь средняя часть стержня длиной находится в тех же условиях, что и шарнирно закрепленный по концам стержень. Поэтому, подставляя здесь вместо в формулу Эйлера найдем

–Эйлерова сила для стержня с двумя

защемленными концами

Полученные формулы Эйлера при различных закреплениях концов стержня можно записать в общем виде:

Здесь коэффициент приведения длины.

Приведенная длина стержня.

Для основных случаев закрепления стержней, показанных на рис. 8.3 коэффициент имеет следующие значения :

а) один конец защемлен, другой свободный ;

б) с шарнирными концами ;

в) один конец защемлен, другой шарнирный ;

г) с двумя заделанными концами .

Зная критическую силу, можно найти критическое напряжение, поделив силу на площадь. Так как на деформации стержня местные ослабления площади сечения (отверстиями) сказываются мало, то при расчетах на устойчивость принято использовать полную площадь сечения. Следовательно, в формуле Эйлера . Тогда

Окончательно

гибкость стержня . (8.9)

Гибкость стержня важная характеристика стержней при расчетах их на устойчивость. В (8.9) надо подставлять минимальный радиус инерции сечения, поэтому максимальная гибкость. Стержень теряет устойчивость в той плоскости, в которой его гибкость максимальная.

В неочевидных случаях надо вычислить отдельно: гибкость относительно (вокруг) оси и гибкость относительно оси , т.е. в плоскости . Если , то и расчет на продольный изгиб надо вести в плоскости изгиба , а если , то и расчет вести в плоскости . Это очень важно, т.к. в случае ошибки расчет ведут в одной плоскости, а стержень теряет устойчивость в другой плоскости.

Для цилиндрического шарнира (вдоль оси ) относительно оси считается шарнир, а относительно оси можно принять защемление. Однако, следует иметь ввиду, что на практике редко удается осуществить защемление. Достаточно возможности небольшого поворота опорного сечения в защемлении, чтобы оно оказалось в условиях близких к шарнирному опиранию. Поэтому обычно принимают .

Формула (8.8) тоже формула Эйлера для критических напряжений.

Пределы применимости формулы Эйлера. Потеря устойчивости за пределами пропорциональности

Формула Эйлера получена из интегрирования дифференциального уравнения упругой оси балки, т.е. предполагалось, что стержень работает в пределах упругих деформаций по закону Гука. Недаром в формуле Эйлера фигурирует модуль Юнга Е .

Следовательно, формулой Эйлера нельзя пользоваться для оценки устойчивости стержней, если критические напряжения, вычисленные по ней, получаются выше предела пропорциональности (где закон Гука не применим).

Итак, формула Эйлера применима при соблюдении условия

Или , откуда

Здесь правая часть представляет наименьшее (предельное) значение гибкости стержня, при котором можно пользоваться формулой Эйлера и обозначается

(8.10)

Условие применимости формулы Эйлера тогда примет вид:

Для Ст.3 и .

Для Ст.5 и .

Для чугуна .

Для дерева .

При гибкости стержня, меньше предельной, критическое напряжение, определенное по формуле Эйлера, получается значительно выше .

Например, при (Ст.3) , т.е. величина оказывается значительно больше предела прочности.

Ошибочное использование формулы Эйлера для вычисления и проверки устойчивости при малых гибкостях, приводили иногда к серьезным катастрофам сооружений. Итак, решение Эйлера применимо на практике лишь для тонких и длинных стержней с большой гибкостью. Между тем на практике часто встречаются стержни с малой гибкостью.

Опыты показали, что если по Эйлеру , то действительные критические напряжения значительно ниже определенных по Эйлеру.

Важнейшим источником для установления действительных критических напряжений за пределом пропорциональности, т.е. при малых и средних гибкостях, явились результаты эксперимента.

Стержни, для расчета на устойчивость которых нельзя пользоваться формулой Эйлера, можно разбить на две большие группы:

1) Стержни с малой гибкостью

Для таких стержней нельзя говорить о явлении потери устойчивости прямолинейной формы стержня в том смысле, как это имеет место для тонких и длинных стержней. Эти короткие стержни будут выходить из строя главным образом от потери прочности, т.е. напряжения сжатия в них достигнут (для пластичных) или (для хрупких) материалов.

Поэтому для коротких толстых стержней , за критические напряжения принимают:

2) Стержни средней гибкости

Для конструкционной Ст.3 . С подобными значениями гибкости инженер чаще всего встречается на практике.

Эти стержни при сжатии теряют свою прямолинейную форму и разрушаются от продольного изгиба. В опытах для них можно отметить наличие ясно выраженной критической силы в Эйлеровом смысле . Для таких стержней критические напряжения получаются выше предела пропорциональности и ниже предела текучести материалов.

На основании обширного опытного материала, собранного профессором Ф. Ясинским, им была предложена эмпирическая формула для определения критических напряжений подобных стержней

– формула Ясинского (8.13)

На основании всего вышесказанного можно построить график критических напряжений (в зависимости от гибкости) для любого материала.

Для конструкционной Ст.3 с кг/см 2 и кг/см 2 этот график (диаграмма) имеет вид, показанной на рис. 8.4. На этом графике четко выделяется три зоны.

x A = 0,5 м, y A = 0,5 м, z A = 0.

F x = − F cosβcos 45D = − 40 0,87 0,707= − 24,5 Н;

F y = − F cosβcos 45D = − 24,5 Н;F z = F sin β= 20 Н.

M ox (F ) = 0,5 20− 0(− 24,5) = 10 Н м;

M oy (F ) = 0(− 24,5)− 0,5 20= − 10 Н м;

M oz (F ) = 0,5(− 24,5)− 0,5(24,5) = 0;

M o (F ) = (M ox (F ))2 +(M oy (F ))2 =14,14 Н м.

II способ. Определим моменты силыF относительно осей координат по формуле (9).

СпроектируемсилуF наплоскость, перпендикулярноосямX ,Y ,Z :

F xy = F cosβ= 17,32Η , F xy OZ ,

Fzy = Fsinβ = 20 Н, Fzy OY, Fzy OX.

M x (F ) = 0,5F zy = 10 Н м,

M y (F ) = − 0,5F zy = − 10 Н м,

М Z (F )= OF XY = 0 (так какF XY пересекает осьZ , то момент силыF относительно осиZ равен нулю).

Результаты, полученные обоими способами, совпадают.

M x (F) = Mox (F) = 10 Н м, My (F) = Moy (F) = − 10 Н м,

МZ (F) = МOZ (F) = 0 ,

M o (F ) = 14,14 Н м.

Вопросы для самоконтроля

1. Сформулируйте определение алгебраического момента силы относительно точки.

2. Как определить плечо силы относительно точки?

3. В каком случае момент силы считают положительным, а в каком – отрицательным?

4. Сформулируйте определение момента силы относительно оси.

5. В каких случаях момент силы относительно оси равен нулю?

Система cходящихcя сил

Приведение системы сходящихся сил к равнодействующей

Силы, линии действия которых пересекаются в одной точке, на-

зываются сходящимися силами.

Исследование систем сходящихся сил выполняется при решении ряда практических задач, в числе которых расчет ферм.

Теорема о равнодействующей системы сходящихся сил. Сис-

тема сходящихся сил эквивалентна одной силе, которая равна геометрической сумме всех этих сил и проходит через точку пересечения их линий действия.

Теорема о равновесии тела , находящегося под действием системы сходящихся сил.

Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая, а, следовательно, и главный вектор этих сил были равны нулю.

Воспользовавшись выражением проекций равнодействующей через проекции сил системы, получаем аналитические условия равновесия:

∑ F kx= 0, ∑ F ky= 0, ∑ F kz= 0.

Равенства (3) выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

Теорема о трех силах . Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

При решении задач на равновесие несвободного твердого тела под действием сходящейся системы сил необходимо придерживаться следующей последовательности.

1. Изобразить исследуемые тела с наложенными на них механическими связями.

2. Показать все действующие на тело активные силы и реакции связей.

3. Выбрать систему координат так, чтобы они составляли известные или легко определяемые углы со всеми векторами рассматриваемых сил.

4. Записать условие равновесия, соответствующее полученной системе сил, то есть спроектировать на оси координат активные силы и реакции связей и приравнять их к нулю.

Пример решения задач

Задача 1. Груз 1 весаP подвешен на гибком нерастяжимом тросеOB , отклоненном от вертикали на угол α, и удерживается в равновесии с помощью другого гибкого нерастяжимого тросаBAC , обхватывающего идеальный блокA и несущего на свободном конце груз 2 (рисунок 21). Считая, что при рав

Рисунок 21 новесии участок тросаAB горизонтален, определить весQ груза 2 и натяжение тросаOB . Размерами груза 1 и весом тросов пренебречь.

Решение. Поскольку заданные и искомые силы действуют на груз 1, это тело является узловым. Поэтому на рисунке показыва-

ются силы, действующие на него: активная сила Р и силы реакции

нити Т ОВ иТ АВ .

Tg30 D ,

По условию трение на блоке отсутствует, поэтому T AB = Q . На тело 1 действует система сходящихся сил, лежащих в одной плоскости, поэтому составляем два уравнения равновесия:

Σ F kx = 0;Т АВ − Т ОВ sin α= 0;Σ F ky = 0;Т ОВ cos α− Р = 0.

Из них находим: Т ОВ = cos Р α иТ АВ = Q = Р tgα.

Задача 2. На середину балкиAB действует силаP . В точкеA балка имеет шарнирно-неподвижную опору, а в точкеB – шарнир- но-подвижную опору (рисунок 22). Определить линию действия реакции в точкеA .

		Рисунок 22

Решение. РеакцияR В шарнирно-неподвижной опоры перпендикулярна опорной поверхности и пересекается с линией действия силыP в точкеC . По теореме о трех непараллельных силах реакция опорыA должна пройти через эту точку:

tgα =		AD = l ,CD = l tg30D ;

tgα = l tg30 l D

α = 30D .

Ответ. Реакция R A образует угол30 D с осью балкиAB .

Вопросы для самоконтроля

1. Дайте определение системы сходящихся сил.

2. Как найти равнодействующую системы сходящихся сил графическим методом?

3. Сформулируйте условие равновесия системы сходящихся сил.

4. Сформулируйте геометрическое условие равновесия системы сходящихся сил.

5. Сформулируйте аналитическое условие равновесия системы сходящихся сил.

6. Сформулируйте теорему о трех непараллельных силах.

Задачи для самостоятельного решения Равновесие плоской системы сходящихся сил

Задача 1. СилыF 1 =F 2 = 10 H иF 3 находятся в равновесии. Линии действия сил между собой образуют углы по 120°.

Определить модуль силы F 3 . (10)

2. Определить модуль силыF 3 на-

тяжение троса BC , если известно, что

натяжение троса AC равноF 2 = 15 H. В положении равновесия углы

α = 30° и β = 75°. (7,76)

3. Определить вес балки AB, если известны силы натяжения веревокF 1

120 H и F 2 = 80 H. Заданы углы α = 45° и β = 30° между вертикалью и веревкамиAC иBC соответственно. (154)

4. Груз удерживается в равновесии стержнямиAC иВС, шарнирно соединенными в точкахА, В иС . СтерженьВС растянут силойF 2 = 45 H, а стерженьАС сжат силойF 1 = 17 H. Определить вес груза, если заданы углы α = 15° иβ = 60°. (18,1)

5. Шарнирный трехзвенник АВС удерживает в равновесии груз, подвешенный к шарнирному болтуС. Под действием груза стерженьАС

сжат силой F 2 = 25 H. Заданы углы α = 60° и β = 45°. Считая стержниАС иВС невесомыми, определить усилия в стержнеВС. (48,3)

6. Груз 1 весом 2 Н удерживается

в равновесии двумя веревками AC иВС , расположенными в вертикальной плоскости. Определить натяжение веревкиВС , если угол α = 30°. (2,31)

7. Два невесомых стержняАС иВС соединены в точкеС и шарнирно прикреплены к полу. К шарнируС подвешен груз1 . Определить реакцию стержняВС , если усилие в стержнеАС равно 43 Н, углы α = 60° и β = 30°. (–24,8)

8. Определить реакцию стержняАС, удерживающего в равновесии груз1 весом 14 Н с помощью цепи, намотанной на барабанD и перекинутой через блокС , еслиуголα = 30°. (–24,2)

9. Груз1 весом 20 Н, подвешенный на канате, удерживается в равновесии стержнямиАО иВО , расположенными в вертикальной плоскости. Другой конец каната закреплен в точкеС. Определить реакцию стержняОА , если углы α = 40° и β = 45°.

							10. Груз		весом 10 Н	подвешен
							с помощью каната, перекинутого че-
							рез блок С и намотанного на барабан
									Определить
							в стержне	АС , если углы
							и β = 60°. (–26,4)

11. Шар1 весом 16 Н и шар2 связа-

ны нитью, перекинутой через блок D , и удерживаются в равновесии. Определить вес шара2 , если угол α = 30°.

12. Пластина весомG = 8 Н удерживается в равновесии двумя канатамиАВ иCD, расположенными в вертикальной плоскости. Определить натяжение канатаCD , если угол

13. Два стержняАС иВС соединены шарнирно в точкеС , к которой через блокD подвешен груз1 весом 12 Н. Определить реакцию стержняВС,

если угол α = 60°. (–6)

14. Груз1 весом 6 Н удерживается

шарнирно в точке С. Определить реакциюстержняАС , еслиуголα= 60°, усилиевстержнеВС равно6,94 Н. (–3,45)

15. Однородный шар весом 12 Н удерживается в равновесии на гладкой наклонной плоскости с помощью веревки АВ. Определить давление шара на плоскость, если угол α = 60°. (10,4)

16. Однородный шар 2 весом 36 Н опирается на ролики1 и3 . Определить давление шара на ролик1 , если угол α = 45°. (25,5)

17. Однородный шар весом 40 Н опирается на две плоскости, пересекающиеся под углом α = 60°. Определить давление шара на наклонную плос-

кость. (46,2)

18. Цилиндр весомG удерживается

в равновесии с помощью веревки АВ.

Нормальная

опорной по-

верхности

40 H.

Определить

натяжение веревки

Если известны

углы α = 45°, β = 30°. (56,6)

19. Грузы весом

дятся в равновесии. Известны вес груза G = 55 H и углы α = 45°,

β = 30°. Определить вес груза G 3 . (61,3)

20. Два груза весомG 1 иG 2 находятся в равновесии. Определить натяжение веревкиВС, если известны вес грузаG 2 = 90 H и углы α = 45°,

β = 30°. (73,5)

21. Горизонтальный брус весом

200 Н удерживается в равновесии с помощью шарнира В и веревкиDE , образующей угол α = 150° со сторонойBD . Определить реакцию шарнираB , если известно соотношение линейных размеров – 4АВ = АС . (200)

22. Один конец стержня АВ закреплен шарнирно в точкеА. К другому концуB привязан груз1 весом 50 Н. Стержень удерживается в равновесииВС. Определить реакцию веревкиВС,

если угол α = 30°. (86,6)

23. Вес однородной горизонтальной балки АВ равен 180 Н. Задан угол α = 45°. Определить реакцию шарни-

ра А. (127)

24. Изогнутый стержень АВС прикреплен к полу посредством шарнираА , а другой его конецС свободно опирается на гладкую поверхность, образующую угол α = 45°. Определить реакцию шарнираА, если на стержень действует силаF = 10 Н. (7,07)

			25. Один конецА криволинейного
			бруса АВ весом 5 Н закреплен в шар-
			нире А, а к другому концуВ привяза-
			на веревка ВС . Определить реакцию
			шарнира А, если угол α = 45°. (3,54)

Сложение и разложение сходящихся сил в пространстве

1. По заданным проекциям силы F на оси координат:F x = 20 H,F y = 25 H иF z = 30 H, определить модуль этой силы. (43,9)

2. Определить косинус угла между вектором силы F и осью ко-

ординат O z , если сила (Н)F = 3 i + 4 j + 5 k . (0,707)

4. Определить косинус угла между вектором силы (Н) F = 3 i + 2,45 j + 7 k и осью координатOx . (0.375)

4. Модуль равнодействующей

силы R пространственной системы сходящихся сил равен 150 Н. Определить ее проекцию на координатную

ось O y , если даны углы

α = 30°, β = 60°. (65)

5. Определить модуль равнодействующей силF 1 = 12 Н,

F 2 = 10 Н иF 3 = 9 Н, приложенных в точкеА , как пока-

зано на рисунке. (18,0)

6. Определить модуль равнодействующей силF 1 = 15 Н,

F 2 = 20 Н иF 3 = 25 Н. Углы,

образованные линиямиG действия силF 1 иF 3 с осями

координат, заданы: α = 60°,

β = 45°. (50,5)

7. Направление равнодействующей трех силR = 33,8 Н задано косинусами направляющих углов:cos (R x ) = 0,325; cos (R y ) = 0;

cos (R z ) = 0,946. Проекции силF 1 иF 2 на координатные оси соответственно равны:F 1 x = 7 Н;F 1 y = 10 Н;F 1 z = 0;F 2 x = – 5 H;

F 2 y = 15 Н;F 2 z = 12 Н. Определить модуль силыF 3 . (32,6)

8. Определить модуль равнодействующей трех сходящихся сил, если заданы их проекции на оси координат:F 1 x = 7 Н;F 1 y = 10 Н;

F 1 z = 0;F 2 x = – 5 Н;F 2 y = 15 Н;F 2 z = 12 Н;F 3 x = 6 Н;F 3 y = 0;F 3 z = – 6 Н. (26,9)= 12 кН,F 3 = 9 кН и угол β = 60°. (20,9)

Равновесие пространственной системы сходящихся сил

1. СилыF 1 =F 2 =F 3 = 30 H направлены по трем взаимно перпендикулярным осям координат. Могут ли они быть уравновешены

силой F 4 = 51,96 Н? (Да)

2. Груз1 весом 60 Н удержива-

ется в равновесии стержнями АС,

ВС иDC, шарнирно соединенны-

ми в точке С , и веревкой, пере-

брошенной через блок Е под

углом α = 60°. Определить усилие в стержне DC, если угол

β = 45°. (–73,5)

3. Три стержняАС, ВС иDC соединены шарнирно в точкеC . ОпределитьусилиевстержнеDC , если заданы силаF АО, ВО иСО соединены в шарниреО . Определить реакцию стержняСО , возникающую под действием силыF = 12 H, приложенной

к шарниру О , если расстояния

AB = AO= AD .(13,9)

9. Тристержня АО, ВО иСО шар- нирно-стержневой конструкции соединены в точкеО, к которой приложена силаF = 18 H. Определить усилие в стержнеАО,

если углы α = 60°, β = 45°. (–25,5)

10. Определить усилие в невесомом стержне CD , если дан вес

груза G = 200 Н, известны длины сторон шарнирно-стержневой конструкцииCE = BE = 2 м

иAB =BD = 4 м. (–127)

38KL+ F2 (KL+ h) = F2 h.

Из полученного выражения видно, что результат не зависит от расстояния KL (следовательно, от положения точкиK ), а определяется только расстояниемh . Расстояниеh между линиями действия сил пары называютплечом пары .

Момент пары считается положительным, если она стремится повернуть тело при действии на него против хода часовой стрелки, иотрицательным – еслиповоротпроисходитпоходучасовойстрелки.

На расчетных схемах для обозначения пар сил применяются символы:

Свойства пары сил

1. Не нарушая действия пары сил на абсолютно твердое тело, ее можно повернуть в своей плоскости на произвольный угол.

2. Не изменяя действия пары на твердое тело, можно менять величину входящей в нее силы и длину плеча, но так, чтобы момент пары оставался неизменным.

3. Не изменяя действия пары на абсолютно твердое тело, можно менять плоскость пары на любую параллельную ей плоскость.

4. Совокупность пар, как угодно расположенных в пространстве, статически эквивалентна одной паре с моментом, равным векторной сумме моментов слагаемых пар.

Условия равновесия пар

Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы момент эквивалентной (результирующей) пары был равен нулю.

	= ∑		k = 0.

Задача 1. Найти результирующую пару, которая уравновесила бы две пары сил с моментамиM 1 = 14 H·м,M 2 = 40 H·м, приложенные к балкеAB длиной2 м (рисунок 24).

Рисунок 24

Формула Эйлера была получена путем интегрирования приближенного дифференциального уравнения изогнутой оси стержня при определенном закреплении его концов (шарнирно-опертых). Значит, найденное выражение критической силы справедливо лишь для стержня с шарнирно-опертыми концами и изменится при изменении условий закрепления концов стержня.

Закрепление сжатого стержня с шарнирно-опертыми концами мы будем называть основным случаем закрепления. Другие виды закрепления будем приводить" к основному случаю.

Если повторить весь ход вывода для стержня, жестко защемленного одним концом и нагруженного осевой сжимающей силой на другом конце (Рис.2), то мы получим другое выражение для критической силы, а следовательно, и для критических напряжений.

Рис.2. Расчетная схема стержня с жесткозакрепленным одним концом.

Предоставляя право студентам проделать это во всех подробностях самостоятельно, подойдем к выяснению критической силы для этого случая путем следующих простых рассуждений.

Пусть при достижении силой Р критического значения колонна будет сохранять равновесие при слабом выпучивании по кривой АВ . Сравнивая два варианта изгиба видим, что изогнутая ось стержня, защемленного одним концом, находится совершенно в тех же условиях, что и верхняя часть стержня двойной длины с шарнирно-закрепленными концами.

Значит, критическая сила для стойки длиной с одним защемленным, а другим свободным концами будет та,же, что для стойки с шарнирно-опертыми концами при длине :

Если мы обратимся к случаю стойки, у которой оба конца защемлены и не могут поворачиваться (Рис.3), то заметим, что при выпучивании, по симметрии, средняя часть стержня, длиной , будет работать в тех же условиях, что и стержень при шарнирно-опертых концах (так как в точках перегиба С и D изгибающие моменты равны нулю, то эти точки можно рассматривать как шарниры).

Рис.3. Расчетная схема с жесткозакреплеными торцами.

Поэтому критическая сила для стержня с защемленными концами, длиной , равна критической силе для стержня основного случая длиной :

Полученные выражения можно объединить с формулой для критической силы основного случая и записать:

здесь - так называемый коэффициент длины, равный:

Для стержня, изображенного на рис.4, с одним защемленным, а другим шарнирно-опертым концами, коэффициент оказывается примерно равным , а критическая сила:

Рис.4. Потеря устойчивости стержня с одним жесткозакрепленным и другим шарнирно-опорным торцом

Величина называется приведенной (свободной) длиной, при помощи коэффициента длины любой случай устройства опор стержня можно свести к основному; надо лишь при вычислении гибкости вместо действительной длины стержня ввести в расчет приведенную длину . Понятие о приведенной длине было впервые введено профессором Петербургского института инженеров путей сообщения Ф. Ясинским).

На практике, однако, почти никогда не встречаются в чистом виде те закрепления концов стержня, которые мы имеем на наших расчетных схемах.

Вместо шаровых опор обычно применяются цилиндрические шарниры. Подобные стержни следует считать шарнирно-опертыми при выпучивании их в плоскости, перпендикулярной к оси шарниров; при искривлении же в плоскости этих осей концы стержней следует считать защемленными (с учетом оговорок, приведенных ниже для защемленных концов).

В конструкциях очень часто встречаются сжатые стержни, концы которых приклепаны или приварены к другим элементам, часто еще с добавлением в месте прикрепления фасонных листов. Такое закрепление, однако, трудно считать защемлением, так как части конструкции, к которым прикреплены эти стержни, не являются абсолютно жесткими.

Между тем, достаточно возможности уже небольшого поворота опорного сечения в защемлении, чтобы оно оказалось в условиях, очень близких к шарнирному опиранию. Поэтому на практике недопустимо рассчитывать такие стержни, как стойки с абсолютно защемленными концами. Лишь в тех случаях, Когда имеет место очень надежное защемление концов, допускается небольшое (процентов на 10-20) уменьшение свободной длины стержня.

Наконец, на практике встречаются стержни, опирающиеся на соседние элементы по всей плоскости опорных поперечных сечений. Сюда относятся деревянные стойки, отдельно стоящие металлические колонны, притянутые болтами к фундаменту, и т. д. При тщательном конструировании опорного башмака и соединения его с фундаментом можно считать эти стержни имеющими защемленный конец. Сюда же относятся мощные колонны с цилиндрическим шарниром при расчете их на выпучивание в плоскости оси шарнира. Обычно же трудно рассчитывать на надежное и равномерное прилегание плоского концевого сечения сжатого стержня к опоре. Поэтому грузоподъемность таких стоек обычно мало превышает грузоподъемность стержней с шарнирно-опертыми концами.

Значения критических нагрузок могут быть получены в виде формул типа эйлеровой и для стержней переменного сечения, а также при действии нескольких сжимающих сил.

Лекция № 44. Пределы применимости формулы Эйлера

Казалось бы, что полученные в предыдущих параграфах результаты решают задачу проверки сжатого стержня на устойчивость; остается выбрать лишь коэффициент запаса . Однако это далеко не так. Ближайшее же изучение числовых величин, получаемых по формуле Эйлера, показывает, что она дает правильные результаты лишь в известных пределах.

На рис.1 приведена зависимость величины критических напряжений, вычисленных при различных значениях гибкости для стали 3, обычно применяемой в металлических конструкциях. Эта зависимость представляется гиперболической кривой, так называемой «гиперболой Эйлеpa»:

При пользовании этой кривой надо вспомнить, что представляемая ею формула получена при помощи интегрирования дифференциального уравнения изогнутой оси, т. е. в предположении, что напряжения в стержне в момент потери устойчивости не превосходят предела пропорциональности .

Рис.1. Гиперболическая зависимость критического напряжения от гибкости стержня

Следовательно, мы не имеем права пользоваться величинами критических напряжений, вычисленных по формуле Эйлера, если они получаются выше этого предела для данного материала. Иначе говоря, формула Эйлера применима лишь при соблюдении условия:

Если из этого неравенства выразить гибкость , то условие применимости формул Эйлера получит иной вид:

Подставляя соответствующие значения модуля упругости и предела пропорциональности для данного материала, находим наименьшее значение гибкости, при которой еще можно пользоваться формулой Эйлера. Для стали 3 предел пропорциональности может быть принят равным , поэтому, для стержней из этого материала можно пользоваться формулой Эйлера лишь при гибкости

т. е. большей, чем 100 %

Для стали 5 при формула Эйлера применима при гибкости ; для чугуна - при , для сосны - при и т. д. Если мы на Рис.1 проведем горизонтальную линию с ординатой, равной , то она рассечет гиперболу Эйлера на две части; пользоваться можно лишь нижней частью графика, относящейся к сравнительно тонким и длинным стержням, потеря устойчивости которых происходит при напряжениях, лежащих не выше предела пропорциональности.

Теоретическое решение, полученное Эйлером, оказалось применимым на практике лишь для очень ограниченной категории стержней, а именно, тонких и длинных, с большой гибкостью. Между тем, в конструкциях очень часто встречаются стержни с малой гибкостью. Попытки использовать формулу Эйлера для вычисления критических напряжений и проверки устойчивости при малых гибкостях вели иногда к весьма серьезным катастрофам, да и опыты над сжатием стержней показывают, что при критических напряжениях, больших предела пропорциональности, действительные критические силы значительно ниже определенных по формуле Эйлера.

Таким образом, надо найти способ вычисления критических напряжений и для тех случаев, когда они превышают предел пропорциональности материалов, например, для стержней из мягкой стали при гибкостях от 0 до 100.

Необходимо сразу же отметить, что в настоящее время важнейшим источником для установления критических напряжений за пределом пропорциональности, т. е. при малых и средних гибкостях, являются результаты экспериментов. Имеются попытки и теоретического решения этой задачи, но они скорее указывают путь к дальнейшим исследованиям, чем дают основания для практических расчетов.

Прежде всего надо выделить стержни с малой гибкостью, от 0 примерно до 30-40; у них длина сравнительно невелика по отношению к размерам поперечного сечения. Например, для стержня круглого сечения гибкости 20 соответствует отношение длины к диаметру, равное 5. Для таких стержней трудно говорить о явлении потери устойчивости прямолинейной формы всего стержня в целом в том смысле, как это имеет место для тонких и длинных стержней.

Эти короткие стержни будут выходить из строя главным образом за счет того, что напряжения сжатия в них будут достигать предела текучести (при пластичном материале) или предела прочности (при хрупких материалах). Поэтому для коротких стержней, до гибкости примерно 30 40, критические напряжения «будут равны, или немного ниже (за счет наблюдающегося все же некоторого искривления оси стержня), соответственно или (сталь), или (чугун, дерево).

Таким образом, мы имеем два предельных случая работы сжатых стержней: короткие стержни, которые теряют грузоподъемность в основном за счет разрушения материала от сжатия, и длинные, для которых потеря грузоподъемности вызывается нарушением устойчивости прямолинейной формы стержня. Количественное изменение соотношения длины и поперечных размеров стержня меняет и весь характер явления разрушения. Общим остается лишь внезапность наступления критического состояния в смысле внезапного резкого возрастания деформаций.

В сжатых стержнях большой гибкости, для которых применима формула Эйлера, после достижения силой Р критического значения обычно наблюдается резкий рост деформаций. До этого момента прогибы, как правило, растут с ростом нагрузки, но остаются незначительными. Теоретически можно было бы ожидать, что до критической силы стержень будет оставаться прямым; однако ряд неизбежных на практике обстоятельств - начальная кривизна стержня, некоторый эксцентриситет приложения нагрузки, местные перенапряжения, неоднородность материала - вызывают небольшие прогибы и при сжимающих силах, меньших критических.

Подобный же характер имеет и зависимость укорочений от напряжения при сжатии коротких стержней; мы имеет ту же внезапность роста деформаций при определенной величине напряжений (когда ).

Нам остается теперь рассмотреть поведение сжатых стержней при средних величинах гибкости, например для стальных стержней при гибкостях от 40 до 100; с подобными значениями гибкостей инженер чаще всего встречается на практике.

По характеру разрушения эти стержни приближаются к категории ^ тонких и длинных стержней; они теряют свою прямолинейную форму и разрушаются при явлениях значительного бокового выпучивания. При опытах для них можно отметить наличие ясно выраженной критической силы в «эйлеровом» смысле; критические напряжения получаются выше предела пропорциональности и ниже предела текучести для пластичных и предела прочности для хрупких материалов.

Однако потеря прямолинейной формы и понижение критических напряжений по сравнению с короткими стержнями для этих стержней «средней» гибкости связаны с такими же явлениями нарушения прочности материала, какие вызывают потерю грузоподъемности в коротких стержнях. Здесь комбинируются и влияние длины, понижающее величину критических напряжений, и влияние значительного роста деформаций материала при напряжениях за пределом пропорциональности.

Экспериментальное определение критических сил для сжатых стержней производилось неоднократно как у нас, так и заграницей. Особенно обширный опытный материал собрал проф. Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в. зависимости от гибкости для целого ряда материалов и положивший начало современным методам расчета сжатых стержней на устойчивость.

На основании полученного опытного материала можно считать, что при критических напряжениях, меньших предела пропорциональности, все эксперименты подтверждают формулу Эйлера для любого материала.

Для стержней средней и малой гибкости были предложены различные эмпирические формулы, показывающие, что критические напряжения при таких гибкостях меняются по закону, близкому к линейному:

где а и b - коэффициенты, зависящие от материала, a - гибкость стержня. Для литого железа Ясинский получил: а = 338,7МПа , b = 1,483 МПа . Для стали 3 при гибкостях от = 40 до = 100 коэффициенты а и b могут быть приняты: а = 336 МПа ; b = 1,47МПа . Для дерева (сосна): а = 29,3 МПа ; b = 0,194 МПа.

Иногда удобны эмпирические формулы, дающие для неупругой области изменение критических напряжений по закону квадратной параболы; к ним относится формула

График состоит из трех частей: гиперболы Эйлера при , наклонной прямой при и горизонтальной, или слабо наклонной, прямой при . Подобные же графики можно построить, комбинируя формулу Эйлера с результатами экспериментов, и для других материалов.