Плоские рамы. Расчет статически определимых рам
Как отмечалось выше, рамы на двух шарнирно-неподвижных опорах с одним промежуточным шарниром также являются статически определимыми.
Пример 10. Рассмотрим построение эпюрдля рамы с промежуточным шарниром (рис.14,а)
В дополнение к условиям равновесия,
рассмотренным в примерах 8 и 9, здесь
для определения неизвестных реакций
 используются еще два условия:
используются еще два условия: и
и , каждое из которых по своей сути выражает
факт равенства нулю изгибающего момента
, каждое из которых по своей сути выражает
факт равенства нулю изгибающего момента в промежуточном шарнире С (рис.14,а).
в промежуточном шарнире С (рис.14,а).
Для определения четырех неизвестных реакций возможно использование различных комбинаций уравнений равновесия, но чаще всего используются следующие уравнения:

При этом для проверки вычисленных реакций служат уравнения:

При заданных нагрузках (рис.14,а) уравнения равновесия принимают вид:

Знак "-", полученный при вычислении
реакции
 ,
говорит о необходимости изменить
принятое для нее направление на
противоположное (перечеркнутая стрелка
на рис.15,а).
,
говорит о необходимости изменить
принятое для нее направление на
противоположное (перечеркнутая стрелка
на рис.15,а).

Рис 14.
Проверяем правильность вычисления опорных реакций.
Теперь вычисляем значения
 в характерных сечениях, выбирая для
сечений 1-8 левую отсеченную часть, а
для сечений 9-14 - правую.
в характерных сечениях, выбирая для
сечений 1-8 левую отсеченную часть, а
для сечений 9-14 - правую.
Из рассмотрения левой отсеченной части:

(сжаты правые волокна стойки);

(сжаты нижние волокна ригеля);
Вновь подчеркнем, что знаки "+" и
"-" для изгибающих моментов
 принимаются относительно, то есть для
разграничения противоположно направленных
моментов, а эпюра
принимаются относительно, то есть для
разграничения противоположно направленных
моментов, а эпюра строится со стороны сжатых волокон.
строится со стороны сжатых волокон.
Из рассмотрения правой отсеченной части:

(сжаты верхние волокна ригеля)
(сжаты правые волокна стойки)

Эпюры
 ,
построенные по вычисленным значениям,
приведены на рис.14,б,в,г.
,
построенные по вычисленным значениям,
приведены на рис.14,б,в,г.
1.17 Построение эпюр в плоско-пространственных системах
Систему, состоящую из прямолинейных стержней, жестко соединенных между собой, расположенных в одной плоскости и нагруженных перпендикулярно к этой плоскости, будем называть плоско-пространственной.
В настоящем пособии будем рассматривать только жесткозащемленые плоско-пространственные системы (далее сокращенно: ППС). При этом возможны два основных варианта:
система располагается горизонтально, нагрузки приложены в вертикальных плоскостях (рис.15,а.,б),
система располагается в вертикальной плоскости, нагрузки приложены горизонтально (рис.15,в,г)
В первом случае (рис.15,а,б) в поперечных
сечениях стержней системы могут
возникать поперечная сила
 ,
изгибающий момент
,
изгибающий момент и крутящий момент
и крутящий момент ;
во втором случае -
;
во втором случае - .
Очевидно, что поворотом на 90 градусов
системы второго вида (рис.15,в,г) приводятся
к системам первого вида, при этом
.
Очевидно, что поворотом на 90 градусов
системы второго вида (рис.15,в,г) приводятся
к системам первого вида, при этом переходит в
переходит в - в
- в ,
поэтому в дальнейшем ограничимся
рассмотрением систем первого вида.
,
поэтому в дальнейшем ограничимся
рассмотрением систем первого вида.
Известно, что при одновременном наличии
в сечениях изгибаемой стержневой
системы внутренних моментов и внутренних
сил влияние последних на
напряженно-деформированное состояние
системы незначительно (исключение
составляет "короткие" стержни),
поэтому исключим из рассмотрения
поперечную силу
 .
.
Итак, остановимся на правилах построения
эпюр
 и
и для плоско-пространственных систем.
для плоско-пространственных систем.

Рис.15
Пример 11.
Рассмотрим ППС (рис.16,а).
Прежде чем строить для этой системы
эпюры и
и ,
построим эпюры
,
построим эпюры и
и для каждой из четырех возможных нагрузок
(они представлены на схеме), так как
вообще говоря, любые эпюры
для каждой из четырех возможных нагрузок
(они представлены на схеме), так как
вообще говоря, любые эпюры и
и в силу принципа независимости действия
сил будут представлять собой алгебраическую
сумму этих простейших эпюр, построенных
от каждой нагрузки в отдельности, но,
разумеется, с учетом места приложения
нагрузок, их направлений и геометрической
конфигурации системы.
в силу принципа независимости действия
сил будут представлять собой алгебраическую
сумму этих простейших эпюр, построенных
от каждой нагрузки в отдельности, но,
разумеется, с учетом места приложения
нагрузок, их направлений и геометрической
конфигурации системы.
Для достижения максимальной общности
будем считать, что сила
 ,
момент типа
,
момент типа и момент типа
и момент типа (имеется в виду плоскость действия
каждого из них) приложены к концевому
сечению (т.А на рис.16,а), а распределенная
нагрузка приложена к первому от
свободного конца участку стержня
(стержень АВ на рис.16,а). Причем, все
построения будем выполнять в общем
виде, полагая, для наглядности, что a<
l.
(имеется в виду плоскость действия
каждого из них) приложены к концевому
сечению (т.А на рис.16,а), а распределенная
нагрузка приложена к первому от
свободного конца участку стержня
(стержень АВ на рис.16,а). Причем, все
построения будем выполнять в общем
виде, полагая, для наглядности, что a<
l.
Пусть к плоско-пространственной
системе (рис.16,в) приложена только сила
 .
Построим эпюры
.
Построим эпюры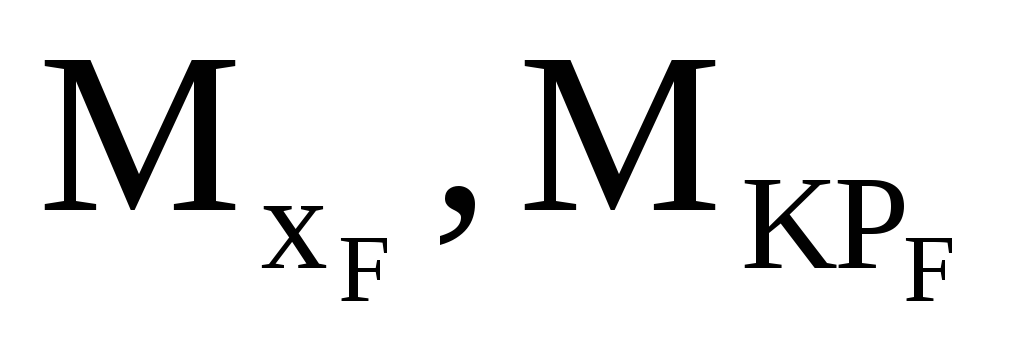 для заданной системы. Здесь, как и при
любой другой внешней нагрузке, более
сложным является построение эпюры
изгибающих моментов
для заданной системы. Здесь, как и при
любой другой внешней нагрузке, более
сложным является построение эпюры
изгибающих моментов .
В соответствии с ранее оговоренными
принципами, для построения эпюры
.
В соответствии с ранее оговоренными
принципами, для построения эпюры в заданной ППС выделим 6 характерных
сечений. Так как имеется жесткая заделка,
то расчет ведем от свободного конца.
При вычислении изгибающего момента
очень важно правильно определить
плоскость изгиба стержня, которому
принадлежит рассматриваемое характерное
сечение, т.к. плечо действующей нагрузки
необходимо определить именно в плоскости
изгиба.
в заданной ППС выделим 6 характерных
сечений. Так как имеется жесткая заделка,
то расчет ведем от свободного конца.
При вычислении изгибающего момента
очень важно правильно определить
плоскость изгиба стержня, которому
принадлежит рассматриваемое характерное
сечение, т.к. плечо действующей нагрузки
необходимо определить именно в плоскости
изгиба.



Рис.16
Стержень АВ изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа;
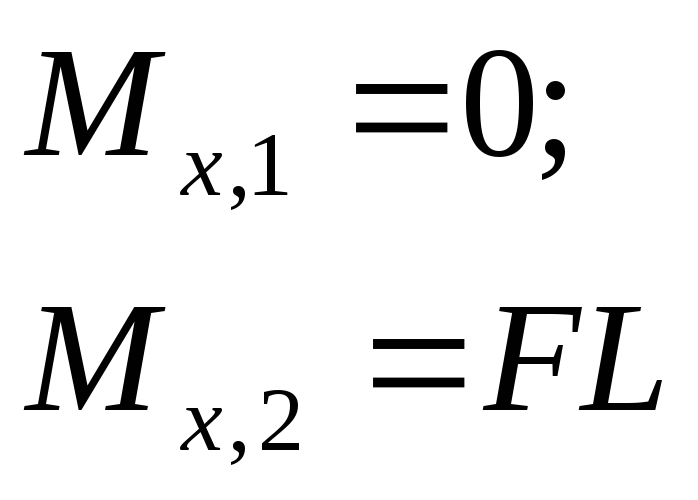 (сжаты верхние волокна).
(сжаты верхние волокна).
Стержень ВС изгибается в вертикальной плоскости, параллельной плоскости чертежа:
 (сила
(сила не имеет плеча в плоскости изгиба!);
не имеет плеча в плоскости изгиба!);
 (сжаты верхние волокна).
(сжаты верхние волокна).
Стержень СД , как и стержень АВ, изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа.
 (сжаты нижние волокна).
(сжаты нижние волокна).
 (сила
(сила не имеет плеча в плоскости изгиба).
не имеет плеча в плоскости изгиба).
Остановимся подробнее на определении
изгибающего момента
 .
Как видно из приведенных выше значений:
.
Как видно из приведенных выше значений: ,
то есть моменты в сечениях 2 и 5 (обратим
внимание на их расположение, а не на
нумерацию, которая, естественно, может
быть совершенно произвольной) одинаковы
по величине, но противоположны по
направлению. Это утверждение можно
доказать.
,
то есть моменты в сечениях 2 и 5 (обратим
внимание на их расположение, а не на
нумерацию, которая, естественно, может
быть совершенно произвольной) одинаковы
по величине, но противоположны по
направлению. Это утверждение можно
доказать.
Причем, возможно как строгое
доказательство, так и некоторые
"нестрогие" рассуждения, приводящие
к тому же факту. Начнем с последних. Под
действием приложенной силы
 (рис.16,в) происходит "перекос"
системы: точка В смещается вверх, а
точка С - вниз; при этом обе точки
располагаются на одинаковом расстоянии
(в вертикальной плоскости, перпендикулярной
плоскости чертежа) от линии действия
силы
(рис.16,в) происходит "перекос"
системы: точка В смещается вверх, а
точка С - вниз; при этом обе точки
располагаются на одинаковом расстоянии
(в вертикальной плоскости, перпендикулярной
плоскости чертежа) от линии действия
силы ,
следовательно, моменты в сечениях 2 и
5 одинаковы, но противоположны по знаку.
,
следовательно, моменты в сечениях 2 и
5 одинаковы, но противоположны по знаку.
Для иллюстрации другого подхода к
"нестрогому" доказательству
утверждения о том, что
 введем в рассмотрение так называемую
скользящую систему координат (рис.16,в).
Такое название связано с тем, что
координатные оси как бы скользят вдоль
ломаной продольной оси системы, не
поворачиваясь вокруг нее. При этом на
каждом участке плоско-пространственной
системы ось z направлена вдоль продольной
оси соответствующего стержня, ось y-
вверх (или вниз) при расположении системы
в горизонтальной плоскости, а ось x
остается перпендикулярной к плоскости
yoz. Как следует из чертежа, на участках
АВ и СД ось x имеет противоположное
направление, следовательно, моменты
введем в рассмотрение так называемую
скользящую систему координат (рис.16,в).
Такое название связано с тем, что
координатные оси как бы скользят вдоль
ломаной продольной оси системы, не
поворачиваясь вокруг нее. При этом на
каждом участке плоско-пространственной
системы ось z направлена вдоль продольной
оси соответствующего стержня, ось y-
вверх (или вниз) при расположении системы
в горизонтальной плоскости, а ось x
остается перпендикулярной к плоскости
yoz. Как следует из чертежа, на участках
АВ и СД ось x имеет противоположное
направление, следовательно, моменты имеют на этих участках разные знаки, а
так как сечения 2 и 5 равноудалены от
линии действия силы
имеют на этих участках разные знаки, а
так как сечения 2 и 5 равноудалены от
линии действия силы ,
то очевидно равенство моментов в этих
сечениях по абсолютной величине.
,
то очевидно равенство моментов в этих
сечениях по абсолютной величине.
И, наконец, рассмотрим более строгое
доказательство. Двигаясь от свободного
конца при выборе отсеченной части, мы
получили:
 (сжаты верхние волокна). Определим
момент
(сжаты верхние волокна). Определим
момент в сечении 5, двигаясь при выборе отсеченной
части со стороны жесткой заделки. Для
определения момента таким способом
необходимо знать реакции заделки. При
действии на систему силы
в сечении 5, двигаясь при выборе отсеченной
части со стороны жесткой заделки. Для
определения момента таким способом
необходимо знать реакции заделки. При
действии на систему силы из всех возможных в общем случае
нагружения реакций в жесткой заделке
возникают реакция
из всех возможных в общем случае
нагружения реакций в жесткой заделке
возникают реакция и опорный момент
и опорный момент ,
определяемые из условий равновесия:
,
определяемые из условий равновесия:

Теперь, двигаясь со стороны жесткой заделки, для сечения 5 получим:
 (сжаты нижние волокна), то есть
(сжаты нижние волокна), то есть (момент
(момент не влияет на величину
не влияет на величину ,
так как его плоскость действия
перпендикулярна плоскости изгиба).
,
так как его плоскость действия
перпендикулярна плоскости изгиба).
Очевидно, что подобные рассуждения
можно провести при любой внешней
нагрузке, поэтому в дальнейшем при
построении эпюры
 всегда будем руководствоваться правилом:
изгибающий момент в сечении 5 равен
изгибающему моменту в сечении 2
(опять-таки, имеется в виду положение
сечений, а не их порядковые номера) и
противоположен ему по знаку, при условии,
что на участке 2-5 не приложен сосредоточенный
момент, который для сечения 5 является
изгибающим, то есть момент типа
всегда будем руководствоваться правилом:
изгибающий момент в сечении 5 равен
изгибающему моменту в сечении 2
(опять-таки, имеется в виду положение
сечений, а не их порядковые номера) и
противоположен ему по знаку, при условии,
что на участке 2-5 не приложен сосредоточенный
момент, который для сечения 5 является
изгибающим, то есть момент типа (рис.16,а).
При наличии на участке 2-5 такого момента
равенство ординат по модулю в сечениях
2 и 5 "искажается" на величину
(рис.16,а).
При наличии на участке 2-5 такого момента
равенство ординат по модулю в сечениях
2 и 5 "искажается" на величину в соответствующую направлению
в соответствующую направлению сторону.
сторону.
Теперь построим эпюру
 .
.
Участок АВ не подвержен кручению, так
как сила
 приложена к продольной оси стержня АВ.
Участок ВС закручивается силой
приложена к продольной оси стержня АВ.
Участок ВС закручивается силой с плечом
с плечом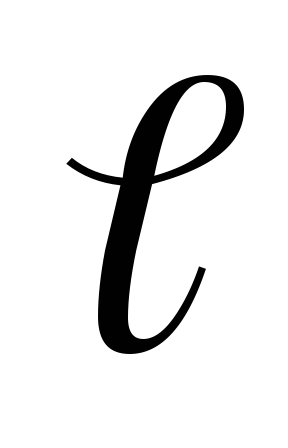 ,
следовательно:
,
следовательно:
 .
.
Участок СД также закручивается силой
 ,
но с плечом
,
но с плечом ,
то есть:
,
то есть:
 .
.
Эпюры
 и
и представлены на рис.16,г.
представлены на рис.16,г.
Аналогичным образом строятся эпюры
изгибающих и крутящих моментов от
распределенной нагрузки
 (рис.16,д),
сосредоточенного момента типа
(рис.16,д),
сосредоточенного момента типа (рис.16,ж)
и сосредоточенного момента типа
(рис.16,ж)
и сосредоточенного момента типа (рис.16,и).
(рис.16,и).
Не останавливаясь детально на построении
этих эпюр, отметим некоторые особенности.
Эпюра
 на участке под распределенной нагрузкой
(и только на этом участке!)- квадратная
парабола, направленная выпуклостью
навстречу нагрузке. На участке СД -
противоположном тому, где приложена
нагрузка
на участке под распределенной нагрузкой
(и только на этом участке!)- квадратная
парабола, направленная выпуклостью
навстречу нагрузке. На участке СД -
противоположном тому, где приложена
нагрузка -
эпюра
-
эпюра пересекает ось в точке, расположенной
напротив равнодействующей распределенной
нагрузки (рис.16,д).
пересекает ось в точке, расположенной
напротив равнодействующей распределенной
нагрузки (рис.16,д).
Анализ эпюр от сосредоточенных моментов
 (рис.16,з)
и
(рис.16,з)
и (рис.16,к)
позволяет сделать очевидный вывод о
том, что если момент приводит к изгибу
какого-либо стержня, то кручение на
этом участке отсутствует и наоборот.
(рис.16,к)
позволяет сделать очевидный вывод о
том, что если момент приводит к изгибу
какого-либо стержня, то кручение на
этом участке отсутствует и наоборот.
Теперь, учитывая накопленный опыт при построении эпюр от раздельного действия каждой из четырех нагрузок, рассмотрим более сложное нагружение (рис.16,а).
При указанных на этом рисунке нагрузках
для построения эпюры
 необходимо выделить 8 характерных
сечений. Двигаясь от свободного конца,
получим по участкам:
необходимо выделить 8 характерных
сечений. Двигаясь от свободного конца,
получим по участкам:
Участок АВ изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа:

(сжаты нижние волокна).
Кручение на участке АВ отсутствует,
так как сила
 и нагрузка
и нагрузка имеют нулевые плечи относительно
продольной оси участка АВ.
имеют нулевые плечи относительно
продольной оси участка АВ.
Участок ВС изгибается в вертикальной плоскости, параллельной плоскости чертежа.
 (сжаты верхние волокна);
(сжаты верхние волокна);
(сжаты нижние волокна);
 ,
так как момент
,
так как момент ,
приложенный к отсеченной части для
сечения 5, действует в плоскости,
перпендикулярной ВС и на изгиб участка
ВС не влияет;
,
приложенный к отсеченной части для
сечения 5, действует в плоскости,
перпендикулярной ВС и на изгиб участка
ВС не влияет;
(сжаты нижние волокна).
Для построения эпюры крутящих моментов
на участке ВС рассмотрим отдельно
участки 3-4 и 5-6, так как между сечениями
4 и 5 приложен момент
 .
Участок 3-4 закручивается силой
.
Участок 3-4 закручивается силой с плечом 3м и в противоположную сторону
- нагрузкой
с плечом 3м и в противоположную сторону
- нагрузкой с плечом 1,5м:
с плечом 1,5м:
(здесь знак "-" носит сугубо условный
характер и может служить только для
обозначения направления кручения).
Участок 5-6 помимо силы и нагрузки
и нагрузки закручивается еще и моментом
закручивается еще и моментом ,
причем, в том же направлении, что и
нагрузкой
,
причем, в том же направлении, что и
нагрузкой ,
поэтому:
,
поэтому:
Участок 7-8 закручивается нагрузкой
 с плечом 2м и в противоположную сторону
- силой
с плечом 2м и в противоположную сторону
- силой с плечом 2м и моментом
с плечом 2м и моментом ,
следовательно:
,
следовательно:
По вычисленным значениям строим эпюры
 и
и (рис.16,б).
(рис.16,б).
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 2 (§ 2.6), гл. 8 (§ 8.9).
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 11 (§ 11.4, 11.5).
Основные определения
Статически определимая рама – конструкция, состоящая из нескольких изгибаемых стержней, закрепленных так, что опорные реакции и внутренние усилия можно найти с помощью уравнений статики. Чаще всего стержни рамы соединены между собой жестким образом, так, что в процессе деформации угол между стержнями не меняется. Мы будем рассматривать только плоские рамы, стержни которых расположены под углом 90°. Вертикальные стержни рамы принято называть стойками, горизонтальные – ригелями. В стержнях плоских рам возникают три внутренних усилия: продольная и поперечная силы и изгибающий момент.
Внутренние усилия в рамах определяются методом сечений, и порядок их нахождения тот же, что и для балок. Напомним, что согласно методу сечений:
·* продольная сила N равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось стержня;
·* поперечная сила Q равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось, перпендикулярную оси стержня;
·* изгибающий момент M равен сумме моментов всех сил, действующих с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения.
Правила знаков для продольной и поперечной сил те же, что и раньше: растягивающая продольная сила положительна, поперечная сила положительна, если она обходит сечение по ходу часовой стрелки. Правило знаков для изгибающего момента в рамах следующее: момент считается положительным, если он изгибает стержень рамы выпуклостью вовнутрь. На эпюрах N и Q положительные значения принято откладывать снаружи, на эпюре М – внутри – со стороны растянутых волокон.
От действия трех внутренних усилий в стержнях рамы возникают напряжения: нормальные и касательные. Нормальные напряжения определяются как сумма напряжений от продольной силы () и от изгибающего момента по формуле (4.1). Касательные напряжения находят по формуле Журавского (4.2).
Перемещения точек оси рамы определяются, как правило, методом Максвелла – Мора по формуле (4.21). Заметим, что произвольная точка оси рамы в отличие от точки оси балки может перемещаться не только по вертикали, но и по горизонтали. Будем обозначать линейные перемещения точек оси рамы буквой d, отмечая направление перемещения индексом сверху: d верт и d гор. Углы поворота сечений рамы, как и балок, обозначаем буквой j.
Примеры решения задач
Определение внутренних усилий в рамах
(задачи № 21, 22)
Условие задачи
Рассмотрим раму, показанную на рис. 4.26, и определим в ней внутренние усилия, то есть построим эпюры N , Q и М .
Решение
Найдем три опорные реакции, используя три уравнения статики. Желательно составлять такие уравнения, чтобы в каждое из них входила бы только одна неизвестная реакция. В данном примере это такие уравнения (предполагаемые направления реакций показаны на рис. 4.27, а ):
проекций сил на вертикальную ось равна 0; ; кН;
Для проверки используем уравнение "сумма проекций сил на горизонталь- ную ось равна нулю":
Находим внутренние усилия, используя метод сечений. Рама имеет три участка. Заметим, что если для балки границей между участками считалось сечение, где появлялся новый силовой фактор, то для рам границей между участками является также и узел, где соединяются соседние стержни рамы (стойка и ригель). Рассечем стержни рамы на трех участках и выберем начало отсчета х на каждом участке (удобно начало отсчета выбирать в начале участка – рис. 4.27, а ). Запишем выражения для продольной, поперечной сил и изгибающего момента на каждом участке, используя вышеприведенные определения этих усилий и правила знаков для них:
участок 1: м;
участок 2: м;
участок 3: м;
Строим эпюры усилий, используя написанные выражения (рис. 4.27, б , в , г ). Значение максимального момента определяем так же, как в балках.
Проверку правильности построения эпюр в рамах производим, проверяя равновесие узлов. Для этого вырезаем узлы (в рассматриваемой раме их два: D и E ) и прикладываем к сечениям, примыкающим к узлам, все внутренние усилия согласно построенным эпюрам. Направление усилий должно соответствовать их знакам. На рис. 4.28 показаны вырезанные из рамы узлы D и E вместе с действующими в сечениях, примыкающих к узлам, внутренними усилиями. Видно, что узлы находятся в равновесии. Из условия равновесия узлов следует, что, если в узле не приложена внешняя пара сил (узел D ), то изгибающие моменты в сечениях, примыкающих к узлу, обязательно одинаковы. То есть, зная изгибающий момент в угловой точке для стойки, можно получить графически ординату М в угловой точке для ригеля, проведя циркулем дугу из вершины угла, как из центра. Если в узле действует сосредоточенная пара сил, то значения изгибающих моментов в примыкающих сечениях отличаются на величину этой пары.
4.2.2. Определение перемещений в рамах (задачи № 21, 22)
Условие задачи
Для рамы, показанной на рис. 4.26, найдем вертикальное перемещение точки В и угол поворота сечения А . Жесткость стержней рамы будем считать одинаковой (). Перемещения ищем методом Максвелла – Мора, интегрируя формулу Максвелла – Мора аналитически и графически (с помощью правила Верещагина).
Решение
Будем искать первое обобщенное перемещение – вертикальное перемещение точки В . В соответствии с методом Максвелла – Мора для определения этого перемещения приложим в точке В единичную вертикальную сосредоточенную силу (рис. 4.29, а ) и найдем изгибающий момент, вызванный этой нагрузкой (координаты , , должны отсчитываться так же, как при определении момента от заданной нагрузки):
участок 1: м;
участок 2: м;
участок 3: м;
Аналогично для определения второго обобщенного перемещения – угла поворота сечения А – приложим в точке А сосредоточенную пару сил, равную единице (рис. 4.29, б ), и определим изгибающий момент от этой пары:
участок 1: м;
участок 2: м;
участок 3: м;
Вариант 1 . Аналитическое интегрирование формулы
Максвелла – Мора
Подставим в формулу Максвелла – Мора (4.21) выражения для изгибающих моментов от заданной нагрузки, найденные ранее при определении внутренних усилий в рассматриваемой раме, умножим их на выражения для изгибающих моментов от единичных обобщенных сил на всех трех участках и выполним интегрирование. Тогда, учтя, что , проинтегрируем формулу (4.21):
250 кН·м 3 ;
–63,3 кН·м 2 .
В соответствии с правилом знаков метода Максвелла – Мора положительный знак вертикального перемещения говорит о том, что точка В перемещается по направлению обобщенной силы, то есть вверх. Сечение А поворачивается по часовой стрелке (в сторону, противоположную направлению единичной пары сил, так как знак угла поворота отрицательный).
Вариант 2 . Интегрирование формулы Максвелла – Мора с помощью правила Верещагина
Построим эпюры моментов от заданной нагрузки М и от единичных обобщенных сил, соответствующих искомым перемещениям, М 1 и М 2 (рис. 4.30). Для перемножения эпюр разобьем эпюру М на 4 простые фигуры: два треугольника w 1 и w 3 , сегмент w 2 и трапецию w 4 . Найдем ординаты под центрами тяжести этих фигур на эпюре М 1 (h 1 , h 2 и h 3 на рис. 4.30, б ). Эпюру М на ригеле, имеющую форму трапеции w 4 с основаниями разного знака, умножаем на трапецию эпюры М 1 по правилу трапеций (4.24). Согласно правилу Верещагина
Аналогично находим угол поворота сечения А , перемножая эпюры М и М 2 . Ординаты под центрами тяжести площадей w 1 , w 2 и w 3 показаны на рис. 4.30, в (h¢ 1 , h¢ 2 и h¢ 3). Для перемножения трапеции w 4 на прямоугольник эпюры М 2 нет необходимости пользоваться правилом трапеций, так как, где бы ни находился центр тяжести трапеции, значение h¢ 4 известно (ординаты на эпюре М 2 на этом участке постоянны).
| Рис. 4.31. Изогнутая ось рамы |
Результаты, полученные по двум вариантам использования формулы Максвелла – Мора, совпадают.
В заключение построим деформированную ось рамы так, чтобы она удовлетворяла эпюре изгибающих моментов и условиям закрепления рамы (рис. 4.31). На рис. 4.31 показаны полученные перемещения – , в соответствии с их направлениями. Точка перегиба (крестик) изогнутой оси ригеля имеет место в сечении, где меняет знак изгибающий момент. Углы рамы в процессе деформации не меняются.
.
4.3. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК И РАМ
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 9 (§ 9.1–9.3).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 9.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 12 (§ 12.1–12.6).
Основные определения
Статически неопределимые балки и рамы – конструкции, в которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему,больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции. Такими связями могут быть как опорные связи, так и стержни самой конструкции. Будем рассматривать балки и простые рамы , то есть такие конструкции, в которых связями, обеспечивающими геометрическую неизменяемость, являются опорные закрепления (опорные связи). Для обеспечения геометрической неизменяемости балки (рамы) в плоскости достаточно трех связей. Каждая связь запрещает какое-то перемещение. Шарнирно-подвижная опора запрещает перемещение по направлению, перпендикулярному плоскости опирания, и является одной связью. Шарнирно-неподвижная опора делает невозможными линейные перемещения по двум взаимно-перпендикулярным направлениям (вертикальному и горизонтальному) и соответствует двум связям, наложенным на конструкцию. Наконец, при наличии жесткого защемления на конце стержня становятся невозможными все перемещения: и вертикальное, и горизонтальное, и угол поворота, поэтому жесткое защемление представляет собой три связи, обеспечивающие геометрическую неизменяемость балки (рамы). Каждая дополнительная связь сверх трех для плоских систем превращает конструкцию в статически неопределимую. Такие дополнительные связи, которые не являются необходимыми для обеспечения геометрической неизменяемости конструкции, называются лишними .
Перед расчетом статически неопределимой конструкции необходимо сначала определить степень статической неопределимости рассматриваемойсистемы. Для балок и простых рам степень статической неопределимости равна числу лишних опорных связей. В каждой связи возникает опорная реакция, поэтому степень статической неопределимости можно найти, сосчитав разность между количеством неизвестных опорных реакций и числом независимых уравнений статики. Например, балка на рис. 4.32, а является один раз статически неопределимой, так как имеет 4 связи и 4 неизвестные опорные реакции, а количество независимых уравнений равновесия – 3. В раме, показанной на рис. 4.34, а , число наложенных связей и опорных реакций в них равно 5, и эта рама является дважды статически неопределимой (в ней две лишние связи). Если в один из стержней балки (рамы) врезан шарнир, то количество связей уменьшается на единицу, так как становится возможным взаимный поворот сечений, примыкающих к шарниру. Появляется дополнительное уравнение для определения опорных реакций: "изгибающий момент в шарнире равен нулю" или можно сказать по-другому: "сумма моментов всех сил, расположенных слева (или справа) от шарнира, равна нулю". Так, балка с врезанным в точке Е шарниром, показанная на рис. 4.33, а , является один раз статически неопределимой: от 5 опорных связей надо вычесть одну связь, связанную с наличием дополнительного шарнира в точке Е . Из четырех оставшихся связей одна является лишней. Можно сосчитать степень статической неопределимости этой балки и иначе: для определения пяти опорных реакций можно составить четыре уравнения статики (дополнительное уравнение "изгибающий момент в шарнире Е равен нулю"). Разность между числом реакций и количеством уравнений статики равна единице, то есть балка один раз статически неопределима.
Рассмотрим один из способов расчета статически неопределимых балок и рам, а именно тот, который основан на том же принципе, что и расчет рассмотренных ранее статически неопределимых стержневых конструкций, работающих на растяжение-сжатие, кручение. Согласно этому способу для определения всех неизвестных к необходимым уравнениям равновесия добавляются уравнения совместности деформаций. При определении деформаций в уравнениях совместности деформаций используются физические уравнения (закон Гука). Из решения полученной системы уравнений можно найти все неизвестные реакции и определить внутренние усилия.
Для уменьшения в системе уравнений количества неизвестных, которые определяются в первую очередь, при расчете балок и рам чаще всего используют прием, связанный с выбором основной системы. Основная система – это статически определимая конструкция, полученная из заданной системы путем отбрасывания лишних связей. Реакции в отброшенных связях принято называть лишними неизвестными и обозначать Х i . Решение задачи (раскрытие статической неопределимости) сводится сначала к определению лишних неизвестных. Для их нахождения используются уравнения совместности деформаций – это условия кинематической эквивалентности основной и заданной систем, то есть равенства, приравнивающие нулю деформации по направлению отброшенных в основной системе связей. Количество уравнений совместности деформаций равно степени статической неопределимости. Зная величины лишних неизвестных, можно найти из уравнений равновесия остальные реакции. Обсудим подробно, как выбирать основную систему и записывать уравнения совместности деформаций.
На рис. 4.32, б , в – 4.34, б , в показаны по два варианта основных систем, выбранных для заданных систем, изображенных на рис. 4.32, а – 4.34, а . Балка на рис. 4.32, а один раз статически неопределима, для выбора основной системы необходимо отбросить одну связь. В первом варианте основной системы, изображенном на рис. 4.32, б , отброшена подвижная опора в точке В . Вертикальная реакция в отброшенной связи (лишняя неизвестная) обозначена буквой Х. Условие совместности деформаций для этого варианта основной системы: – это условие, приравнивающее нулю вертикальное перемещение (прогиб) в точке В балки, так как в заданной системе этот прогиб был невозможен. Во втором варианте на рис. 4.32, в жесткое защемление заменено шарнирно-неподвижной опорой. Лишней неизвестной является реактивный момент. Посколькув точке А стал возможным поворот сечения, то условие совместности деформаций полагает этот угол поворота равным нулю: .
Для выбора основной системы в дважды статически неопределимой раме на рис. 4.34, а требуется отбросить две связи. На рис. 4.34, б , в лишние неизвестные обозначеныХ 1 и Х 2 . В основной системе, показанной на рис. 4.34, б , стали возможны по сравнению с заданной системой горизонтальное перемещение в точке В – и вертикальное перемещение в точке С – , поэтому эти перемещения необходимо приравнять нулю. Это и есть условия совместности деформаций для варианта основной системы, показанной на рис. 4.34, б :
Аналогично для основной системы, изображенной на рис. 4.34, в , условия совместности деформаций следующие: .
Обсудим еще вариант 2 основной системы, показанный на рис. 4.33, в . В точке С сделан разрез стержня и между соседними сечениями вставлен шарнир. Лишней неизвестной в этом случае является изгибающий момент, возникающий в сечении С при отсутствии шарнира. Этот изгибающий момент изображен на рис. 4.33, в в виде двух одинаковых пар сил Х . Чтобы записать уравнение совместности деформаций, надо понять, чем отличается деформация заданной системы от деформации рассматриваемой основной системы. В заданной системе поворот соседних сечений, расположенных бесконечно близко слева и справа от точки С , возможен на один и тот же угол (сечения "склеены"). После разреза и добавления шарнира соседние сечения могут поворачиваться относительно друг друга на угол (рис. 4.35). Этот взаимный угол поворота соседних сечений в точке С мы и должны положить равным нулю при записи условия совместности деформаций: .
Для определения лишних неизвестных необходимо найти деформации в условиях совместности деформаций любым способом. Как правило, деформации находят методом Максвелла – Мора с использованием правила Верещагина. Удобно искать деформации отдельно от заданной нагрузки и от лишних неизвестных . Например, условия совместности деформаций (4.26) можно записать так:
Таким образом, для дважды статически неопределимой системы получаем систему уравнений из двух уравнений с двумя неизвестными, из которых и находим лишние неизвестные. После определения и находим остальные неизвестные реакции и строим окончательные эпюры внутренних усилий N , Q и М , используя уравнения статики.
Окончательную эпюру изгибающих моментов для один раз статически неопределимой системы можно проверить, перемножив ее с эпюрой моментов от единичной силы. Результатом этого перемножения должен быть ноль, то есть
. (4.29)
Условие (4.29) – это условие совместности деформаций, подтверждающее равенство нулю деформаций по направлению лишней неизвестной.
Примеры решения задач
При построении эпюр Q, M и N условимся придерживаться следующих правил:
1. Опорные реакции необходимо показать на схеме всей рамы или отдельных ее частей. Желательно предугадать действительное направление опорных реакций.
Если это не получится и опорные реакции имеют отрицательное значение, то следует изменить их направление на обратное и в последующем учитывать со знаком плюс.
2. При определении составляющих опорных реакций необходимо выбирать рациональный порядок составления уравнений, стремясь к тому, чтобы в каждое уравнение входило возможно меньше неизвестных (лучше по одному).
3. Построение эпюр следует начинать с эпюры изгибающих моментов М .
Ø Изгибающий момент в сечении рамы вычисляется как алгебраическая сумма моментов, относительно центра тяжести сечения, всех сил, приложенных к отсеченной части. Ординаты эпюры изгибающих моментов откладываются со стороны растянутого волокна.
Ø Поперечная сила в сечении рамы вычисляется как алгебраическая сумма проекций сил, приложенных к отсеченной части, на нормаль к оси элемента в рассматриваемом сечении.
Ø Продольная сила в сечении рамы вычисляется как алгебраическая сумма проекций сил, приложенных к отсеченной части, на ось стержня.
Поперечная сила Q считается положительной, если проекция на нормаль к оси стержня равнодействующих сил, приложенных к левой отсеченной части стержня, направлена вверх (по часовой стрелке относительно сечения) (рис.4.2.).
Рис. 4.2. Правило знаков для Q
Ø Продольная сила считается положительной в случае растяжения (рис. 4.3.).
Рис. 4.3. Правило знаков для N
Штриховая линия, проводимая вдоль одной из сторон стержня рамы, условно обозначает низ стержня. Эта линия может быть проведена с любой стороны стержня. Для горизонтальных и наклонных стержней удобно проводить штриховую линию снизу.
Положительные ординаты эпюры М откладываются со стороны штриховой линии, положительные ординаты эпюр Q и N – со стороны, противоположной низу стержня (штриховой линии).
Усилия в стержнях, вплотную примыкающих к узлам рамы, следует обозначать принятыми буквами (М, Q, N ), сопровождая их индексами в соответствии с названием узла и номера стержня.
Например:
M c 2 = –32 кН – изгибающий момент во втором стержне в сечении, примыкающем к узлу С (рис.4.4.).
Рис. 4.4. Эпюра моментов
Q с2 – поперечная сила во втором стержне в сечении, примыкающем к узлу С .
Построение эпюры необходимо проверить как с точки зрения соответствия всех эпюр характеру нагрузок, так и с точки зрения равновесия всех узлов, отдельных частей и всей рамы в целом.
При проверке соответствия всех эпюр характеру нагрузок необходимо руководствоваться следующим:
Для эпюры М :
ü в пределах незагруженного участка прямолинейного стержня эпюра должна изменяться по линейному закону;
ü в месте приложения сосредоточенной силы эпюра имеет излом по направлению действия этой силы;
ü в месте приложения сосредоточенного момента эпюра имеет скачок, равный по величине этому моменту;
ü на участках воздействия равномерной нагрузки эпюра изображается параболой, выпуклость которой обращена в сторону действия нагрузки;
ü в шарнирах изгибающие моменты должны быть равны нулю.
Для эпюры Q :
ü в пределах незагруженного прямолинейного участка стержня значение Q должно быть постоянным;
ü в местах приложения сосредоточенной силы эпюра имеет скачок, равный проекции силы на нормаль к оси стержня;
ü на прямолинейной участке, загруженном равномерной нагрузкой, эпюра меняется по линейному закону;
ü в тех сечениях стержня, где Q равна нулю или меняет знак, изгибающий момент должен иметь максимальное или минимальное значение.
Для эпюры N :
ü в пределах незагруженного прямолинейного участка стержня или при нагрузке, действующей к оси стержня по нормали, значение N должно быть постоянным;
ü в месте приложения сосредоточенной силы, направленной не по нормали к оси стержня, эпюра имеет скачок, равный проекции силы на ось стержня;
ü на прямолинейном участке, загруженном равномерной нагрузкой, если она действует не по нормали к оси стержня, эпюра меняется по линейному закону.
4. При проверке равновесия узлов рамы следует выразить каждый ее узел сечениями, бесконечно близко расположенными к центру узла, приложить к узлу действующие на него сосредоточенные силы, сосредоточенные моменты и усилия М, Q и N, возникающие в поперечных сечениях.
Рекомендуется векторы усилий, действующих на узел, показать с учетом их знаков и с указанием численного значения этих усилий. При этом следует учесть, что направление положительного момента должно быть таким, чтобы вызывать растяжение волокон стержня, отмеченных штриховой линией, положительное значение Q стремится вращать узел по часовой стрелке, а положительное значение N вызывает растяжение.
При равновесии узла уравнения проекций на горизонтальную ось, уравнения проекций на вертикальную ось и уравнения моментов относительно центра узла при подстановке найденных значений усилий должны обращаться в тождества.
5. Эпюры М, Q и N должны быть выполнены с обязательным численным обозначением характерных ординат на концах всех стержней, под сосредоточенными силами и моментами, в середине участка с распределенной нагрузкой.
6. Ось стержня принимается за ось абсцисс. Вычисленные ординаты эпюр откладываются перпендикулярно к оси рассматриваемого стержня. Положительные ординаты эпюры Q откладываются вверх от оси ригеля и влево от оси стойки. Знак на эпюре ставится.
Ординаты эпюры М откладываются со стороны растянутых волокон. Знак на эпюре не ставится.
Ординаты эпюры N откладываются симметрично по обе стороны от оси рассматриваемого стержня. Знак на эпюре N обязателен.
7. Штриховка эпюр производится перпендикулярно к оси стержня.
3. Пример 4.1.
Определить внутренние усилия и построить эпюры М, Q и N в простейшей статически определимой раме, расчетная схема которой представлена на рис.4.5.
l 1 = 6 м; l 2 = 3 м; h 1 = 6 м; h 2 = 6 м;
F = 30 кН q = 2 кН/м
Рис. 4.5. Расчетная схема рамы
1. Проверка статической определимости и геометрической неизменяемости рамы.
Определяем степень свободы системы по формуле:
n = 3Д – 2Ш – С о n , (15)
где n – степень свободы системы;
Д – число дисков;
Ш – число простых шарниров, не считая опорных;
C on – число опорных стержней.
n = 3 · 1 – 2 · 0 – 3 = 0
Степень свободы системы равна нулю. А так как рама представляет собой жёсткий диск, который прикреплен к земле с помощью трех стержней, оси которых не пересекаются в одной точке и не параллельны друг другу, то данная рама является системой статически определимой и геометрически неизменяемой.
2.Определение опорных реакций.
Освобождаем раму от опорных связей, а их действие заменяем реакциями отброшенных связей. Направление реакции шарнирно-неподвижной опоры А заранее указать нельзя, поэтому изображаем две взаимно перпендикулярные составляющие этой реакции Н А и V В.
Реакция шарнирно-подвижной опоры «В» действует по вертикали вверх (рис.4.6.).
Рис. 4.6. Схема определения опорных реакций
Теперь раму можно рассматривать как свободное твердое тело, находящееся в равновесии под действием заданной нагрузки и трех неизвестных, составляющих реакции опор Н А, V A и V В.
Для определения неизвестных необходимо составить три уравнения статики, из совместного решения которых найдутся искомые величины.
Правильным выбором условий равновесия иногда удается уйти от решения системы уравнений, свести задачу к решению независимых уравнений. Так в нашем примере правильным выбором условий равновесия можно добиться того, чтобы в каждое уравнение вошла лишь одна неизвестная величина. Это в значительной степени упростит решение задачи.
1. ∑Х = 0 –Н А = 0 Н А = F = 30 кН
2. ∑М А = 0
3. ∑М В = 0
Проверка. Для проверки правильности найденных значений реакций опор составим уравнения проекций на вертикальную ось:
∑У = 0 –V A – q(l 1 + l 2) + V В = –10,5 – 2(6 + 3) + 28,5 = 0
Произведенная проверка показывает, что реакции опор определены верно. При подстановке в уравнение найденных значений усилий получено тождество.
3. Определение изгибающих моментов и построение эпюры М .
При построении эпюры изгибающих моментов раму необходимо разбить на участки, в пределах которых выражения для изгибающего момента остается неизменным. Выражения для изгибающего момента будут меняться в сечениях, где:
а) приложена сосредоточенная сила или сосредоточенный момент;
б) начинается или заканчивается участок с распределенной нагрузкой;
в) происходит излом оси рамы.
Разбивка рамы на участки показана на рис. 4.7.
Рис. 4.7. Разбивка рамы на участки
Номера участков обозначены цифрами. Штриховыми линиями показаны «нижние» волокна стержней.
Знак изгибающего момента определяется по его воздействию на «нижнее» волокно стержня в пределах рассматриваемого участка. Если «нижнее» волокно под действием изгибающего момента растянуто, то знак плюс, если сжато – минус.
Ординаты эпюры изгибающих моментов откладываются со стороны растянутого волокна.
Рассмотрим определение изгибающих моментов в раме по участкам.
Рис. 4.9. Участок II
М 2 = Н А · У 2 – F(У 2 – 3)
У 2 = 3 м М К2 = 30 · 0 – 30 ·(3 – 3) = 90 кНм
У 2 = 6 м М С2 = 30 · 6 – 30(6 – 3) = 90 кНм
Сила Н А создает положительный момент, сила F – отрицательный.
Характер эпюры – прямая линия.
III участок (рис. 4.10.). 0 м ≤ Х 3 ≤ 6 м;
Рис. 4.10. Участок III
Характер эпюры – кривая второго порядка, так как переменная Х 3 входит в выражение для М 3 во второй степени.
Х 3 = 0 м М С3 = 30 · 8 – 10,5 · 0 – 30 · 3 – 2 · = 90 кН·м
Х 3 = 6м М ДЗ = 30 · 6 – 10,5 · 6 – 30 · 3 – 2 · 6 · = –9 кН·м
Определим значение Х 3 , при котором изгибающий момент М 3 имеет экстремальное значение. Для этого возьмем первую производную от выражения для изгибающего момента М 3 по Х 3 и приравняем ее нулю:
Полученное значение X 3 = –5,25 м лежит за пределами рассматриваемого интервала , поэтому на рассматриваемом участке функция экстремума не достигает. Изгибающий момент монотонно убывает со значения 90 кНм в точке С до – 9 кНм в точке Д.
IV участок (рис. 4.11.).
Рис. 4.11. Участок IV
0 м ≤ Х 4 ≤ 3 м;
Характер эпюры – кривая второго порядка.
Х 4 = 0 м; М Е4 = 0
От оси рамы откладываем найденные значения ординат и соединяем соответствующими линиями.
Рис. 4.13. Эпюра М
Статическая проверка правильности построения эпюры М .
Так как от действия моментов, вызываемых внешними силами, рама в целом находится в равновесии, то к каждая ее часть должна находиться в равновесии. Вырежем последовательно узлы рамы и проверим соблюдение условий их равновесия.
Узел С.
Рис. 4.14. Узел С
∑М С = 0
М С2 – М С3 = 0
90 – 90 = 0
Из эпюры М видно, что в узле С действуют положительные моменты, поэтому при рассмотрении равновесия этого узла векторы моментов прикладываем таким образом, чтобы они вызывали сжатие нижних волокон стержней (рис. 4.14.).
Условия равновесия узла выполнены.
Узел Д.
Рис. 4.15. Узел Д
∑Д = 0
–М Д3 – М Д4 = 0
–90 + 90 = 0
Условие равновесия узла выполнено.
Условия равновесия узлов выполнены, а это свидетельствует о том, что эпюра М построена верно.
4. Определение поперечных сил и построение эпюры Q
При построении эпюры Q раму необходимо разбить на участки. Число участков, которое нужно рассмотреть для построения эпюры поперечной силы, устанавливается так же, как и при построении эпюры изгибающего момента»
I участок
0 м ≤ У 1 ≤ 3 м
Повернув мысленно стержень I до горизонтального положения штриховой линией вниз и рассматривая равновесие левой отсеченной части, получим:
Q 1 = Н Д = 30 кН
Значение поперечной силы по всему участку постоянно, следовательно:
Q А1 = Q К1 = 30 кН
Знак поперечной силы Q 1 – плюс, так как проекция на нормаль к оси стержня силы Н Д , расположенной слева от сечения, направлена вверх.
II участок
3 м ≤ У 2 ≤ 6 м
Q 2 = Н А – F = 30 – 30 = 0
Значение поперечной силы по всему участку постоянно, поэтому:
Q К2 = Q С2 = 0
III участок
0 м ≤ Х 3 ≤ 6 м
Q 3 = –V A – q · X 3
X 3 = 0м; Q С3 = –10,5 – 2 · 0 = –10,5 кН
Х 3 = 6 м; Q Д3 = –10,5 – 2 · 6 = – 22,5 кН
IV участок
0 м ≤ Х 4 ≤ 3 м
Q 4 = q · X 4
Х 4 = 0 м; Q 4 = 0; Х 4 = 3 м; Q 4 = 2 · 3 = 6 кН
V участок
0 м ≤ У 5 ≤ 6 м
Q 5 = 0
По пятому стержню поперечная сила равна нулю, так как отсутствуют силы, которые проектировались бы на нормаль к оси стержня.
На основании полученных данных строим эпюру Q (рис.4.16.). Масштаб: в 1 см 20 кн.
Рис.4.16. Эпюра Q
Проверяем соответствие эпюры М и Q дифференциальной зависимости .
Если функция М возрастет, то первая производная должна быть положительной и наоборот.
I участок : М возрастает от 0 до 90 кнм. Q – положительная.
II участок : М постоянная. Q 2 равна нулю.
III участок : М убывает от 90 кнм до –9 кнм. Q – отрицательная.
IV участок : М возрастает от –9 кнм до 0. Q – положительная.
V участок : М равна нулю. Q 5 – равна нулю.
Вывод: Эпюры М и Q соответствуют дифференциальному соотношению между ними.
5. Определение продольных сил и построение эпюры N .
I участок
Проектируем силы, приложенные к первому участку на направление оси стержня АС.
N 1 = V A = 10,5 кН
Продольная сила N 1 положительная, так как под действием реакции V А стержень АС растянут.
III участок
Проектируем силы, приложенные к рассматриваемой части рамы на направление оси стержня СД .
N 3 = H A – F = 30 – 30 = 0
IV участок
V участок
N 5 = –V В = –28,5 кН
Узел С.
Рис. 4.18. Узел С
∑Fy = 0
Q С3 – N С1 = 0
10,5 – 50,5 = 0
Условие равновесия узла выполнено.
Узел Д.
Рис. 4.19. Узел Д
∑Fy = 0
–Q Д3 – Q Д4 + N Д5 = 0
–22,5 – 6 + 28,5 = 0
Условие равновесия узла выполнено. Эпюры Q и N построены верно.
Вопросы для самопроверки
1. Какие рамы следует отнести к сложным?
2. Каков порядок расчета сложных рам?
3. Как проверить статическую определимость и геометрическую неизменяемость рамы?
4. Как вычисляется изгибающий момент в сечении рамы?
5. Как проверяется правильность очертания эпюры М ?
6. Правило знаков при построении эпюры М .
7. Как вычисляется поперечная сила в сечении рамы?
8. Как проверяется правильность построения эпюры Q ?
9. Правило знаков при построении эпюры Q?
10. Как вычисляется продольная сила в сечении рамы?
11. Как проверяется правильность построения эпюры N ?
12. Правило знаков при построении эпюры N .
13. Дифференциальные зависимости между М и Q .
14. Как по эпюре М определить знак поперечной силы?
15. Как проверяется равновесие узлов рамы, отдельных ее частей и рамы в целом?


