Прогиб условие стыковки дифференциальное уравнение четвертого порядка. Непосредственное интегрирование – практически не имеет ограничений по использованию. возможном перемещении из предполагаемого положения равновесия равнялось нулю

Для определения уравнения оси изогнутой балки воспользуемся :

Выражение для кривизны некоторой кривой:

.

В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому (вторая производная от прогиба представляет собой кривизну изогнутой оси балки (уравнение изгиба ) в рассматриваемом месте балки:.

Продифференцировав полученное уравнение дважды по z, получим : .

Интегрирование дифференциального уравнения оси изогнутой балки

Интегрируя дифференциальное уравнение оси изогнутой балки первый раз, получим выражение, дающее закон изменения поперечной силы по длине балки.

Второе интегрирование определяет характер изменения изгибающего момента.

Третье интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения углов поворота поперечных сечений.

Четвертое интегрирование дифференциального уравнения оси изогнутой балки определяет закон изменения прогибов балки по ее длине.

Постоянные интегрирования определяются из условий закрепления балки.

Упругую линию балки можно рассматривать как график не­которой функции, определяемой характером нагружения балки, ее размерами и материалом. Сама функция представляет собой текущую ординату упругой линии, а ее аргументом является абсцисса центра тяжести произвольного поперечного сечения балки, т. е.

v =Ф(z ). (7.1)

Для определения этой функции воспользуемся зависи­мостью между кривизной К оси балки (кривизной нейтрального слоя) и изгибающим моментом М х и жесткостью сечения балки при изгибе EJ х

К = 1/ρ = M х /(EJ х ) . (7.2)

Из курса математики известно следующее выражение кри­визны некоторой кривой, которое для принятой на рис. 7.1 системы координат запишется в виде

К = , (7.3)

где = dv/dz ; =d 2 v/dz 2 .

Подставляя это значение К в выражение (7.2), получим точное дифференциальное уравнение изогнутой оси балки (упругой линии)

= M х /(EJ х ) . (7.4)

Первая производная от функции дает значение тангенса угла θ наклона касательной к графику этой функции и осью z (см. рис.7.1). В пределах упругих деформаций балки эти углы весьма малы – порядка тысячных долей радиана, поэтому квадратом величины по сравнению с единицей можно пренебречь и принять откуда

=d 2 v/dz 2 = M х /(EJ х ) . (7.5)

Данное выражение называется приближенным дифференциальным уравнением упругой линии. Для балокпостоянного сечения его обычно записывают в виде

EJ х = M х. (7.6)

Правая часть зависимости (7.6) представляет собой уравнение изгибающих моментов т.е. аналитическое выражение закона изменения изгибающего момента по длине балки.

Для вычисления углов поворота θ ≈ и прогибов v необходимо произвести интегрирование уравнения (7.6).

Проинтегрировав уравнение один раз, получим уравнение углов поворота

EJ х = , (7.7)

где С – постоянная интегрирования.

Интегрируя второй раз, получим уравнение прогибов

EJ х v= , (7.8)

где D – вторая постоянная интегрирования.

Постоянные интегрирования С и D определяются из условий опирания балки (граничных условий). Так, для балки, заделанной одним концом (см. рис. 7.1), в месте заделки должны быть равны нулю и прогиб, и угол поворота сечения. Для балки, опертой по концам, прогиб должен быть равен нулю и на левом, и на правом конце.

Определив постоянные интегрирования, можно из уравнений (7.7) и (7.8) определить угол поворота и прогиб любого сечения.

Пример. Двухопорная балка длиной l (рис. 7.2) нагружена силой F, расположенной на расстоянии а от левой опоры. Требуется составить уравнение упругой линии и найти перемещение в сечении на расстоянии z .

Решение. Начало координат располагаем на левой опоре. Опорные реакции R A и R B соответственно составят

R A = F ; R B = F .

Изгибающие моменты на первом и втором участках балки имеют выражения

M 1 = F z , (0 ≤ z ≤ a ); M 2 = F z –F(z –a ), (0 ≤ z ≤ l ).

Дифференциальное уравнение упругой лини балки имеет вид (7.4)

= M х /(EJ х ) .

После однократного интегрирования находим угол поворота сечения балки на опоре А

θ A = = .

Угол поворота на правой опоре B:

После двукратного интегрирования прогиб в сечении на расстоянии z от левой опоры:

при 0 ≤ z ≤ a

v = ;

при 0 ≤ z ≤ l

v = .

Так как поперечная сила Q имеет разрыв первого рода в точке z=a, то функции M , q , n не могут быть выражены аналитически одним выражением.

Постоянные интегрирования, вошедшие в приведенные выше выражения, определены из граничных условий (условий закрепления балки).

Оборудование, приборы и материалы: лабораторная установка,подвеска с набором грузов, индикаторы часового типа, штангенциркуль, линейка.

Описание установки

Схема установки приведена на рис. 7.2 . Как видно из схемы левая опора А балки 1 прямоугольного поперечного сечения является шарнирнонеподвижной, а правая В – шарнирноподвижной. Материал балки – сталь, Е= 2∙10 5 МПа, размеры поперечного сечения: ширина b 1 , толщина h.

Рис. 7.2. Схема лабораторной установки

С левым концом балки 1 жестко соединена планка АC длиной на балку 1 создается подвеской 2 с набором грузов 3. Подвеска может перемещаться вдоль балки и крепиться на ней в любом сечении. Прогиб балки фиксируется индикатором 4, корпус которого крепится к подвижной стойке, что позволяет перемещать его вдоль балки и производить измерения в любом ее сечении. Величина угла поворота θ сечения балки на опоре А после приложения нагрузки F приближенно определяется через смещение Δ С точки С, фиксируемое индикатором 5, корпус которого закреплен на опоре. Так как при изгибе балки в пределах упругих деформаций угол поворота сечения мал, можно с достаточной степенью точности считать длину дуги, описываемой при деформации балки точкой С, примерно равной ее хорде Δ С. Тогда центральный угол θ этой дуги составит

θ ≈ Δ С / r.

Порядок проведения работы

1. Ознакомиться с лабораторной установкой, зарисовать схему нагружения испытываемой балки, записать размеры длин участков (l , а, АС=r ) и поперечного сечения (h , b ).

2. В сечении балки, указанном преподавателем, закрепить подвеску 2 (см. рис. 7.2).

3. Установить стойку с индикатором 4 в одном из сечений, в которых будет замеряться прогиб балки (z 1 = l /4; z 2 = l / 2; z 3 =a ).

4. Поворотом ободков индикаторов 4 и 5 выставить их показания на ноль.

5. Установить на подвеску набор грузов 3, обеспечив заданную преподавателем нагрузку F. Записать показания соответствующих индикаторов (v эксп , Δ С) в таблицу 7.1.. Рассчитать значение θ.

6. Снять с подвески грузы, передвинуть стойку с индикатором 4 на следующее сечение балки; обнулить показания индикатора 4, затем установить снятые грузы на подвеску и записать показания индикатора в таблицу 7.1.

7. Выполнить действия в соответствии с п. 6 для всех сечений балки, где необходимо определить прогибы, и записать показания индикатора в таблицу 7.1.

9. Произвести теоретический расчет угла поворота сечения θ на опоре А и прогибов v теор для тех же сечений, что и при экспериментальном определении (т.е. при z 1 = l /4; z 2 = l /2; z 3 =a ).

10. Вычислить расхождение в процентах между расчетными и опытными значениями угла поворота и прогибов.

11. По данным теоретического расчета построить в масштабе упругую линию балки.

Таблица 7.1

z , мм	v эксп , мм	v теор , мм	Δ С, мм	θ экпп , рад	θ теор , рад
z 1 = l /4 =
z 2 = l /2 =
z 3 =a =

Вопросы для самопроверки

1. Что называется балкой?

2. Что такое прогиб, стрела прогиба?

3. Что понимается под упругой линией балки?

4. Что такое угол поворота сечения балки?

5. В каком случае изгиб балки считается прямым?

6. Что называется жесткостью балки при изгибе?

7. В какой точке расположен центр изгиба (центр инерции) однородной балки с поперечным сечением, показанным на рисунке?

8. Какая из балок имеет большую жесткость (материал одинаковый)?

9. Во сколько раз изменится прогиб балки в исследованной Вами точке, если балку развернуть вокруг своей оси на 90°?

10. Во сколько раз изменится прогиб балки в исследованной Вами точке, если все линейные размеры балки пропорционально увеличить в 2 раза, а вес груза и материал балки оставить неизменным?

11. Какие внутренние силовые факторы действуют в сечениях балки при чистом изгибе?

иографический список

1. Степин П.А. Сопротивление материалов: учебник для немашиностроительных специальностей вузов / П.А.Степин. – М.: Высш. школа, 1988.– 366 с.

2. Копнов В. А. Сопротивление материалов: руководство для решения задач и выполнения лабораторных и расчетно-графических работ / В. А. Копнов. – М. : Высш. школа, 2003. – 351 с.

3. Рубашкин А. Г. Лабораторные работы по сопротивлению материалов /А.Г. Рубашкин – М. : Высш. школа, 1982. – 240 с.

4. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев; отв. ред. Г. С.Писаренко. – 2-е изд., перераб. и доп. – Киев: Наукова думка, 1988. – 736 с.

5. Афанасьев А. М. Лабораторный практикум по сопротивлению материалов / А. М. Афанасьев, В. А. Марьин. – М. : Наука, 1975. – 284 с.

6. Кирносов В.Н. Измерение механических характеристик материалов. уч. пособие/ В.Н. Кирносов.– М.: Изд-во стандартов, 1976. – 240 с.

7. Феодосьев В. И. Сопротивление материалов / В. И. Феодосьев. – М. : Наука, 1999. – 456 с. (МГТУ им. Баумана, 2005. 591 с).

8. Электрические измерения электрических и неэлектрических величин / под ред. Е. С. Полищука. – Киев: Вища школа, 1984. – 359 с.

ПРИЛОЖЕНИЯ

Приложение 1.

Механические характеристики сталей (по ГОСТ 380–94)

Марка стали	Термообработка	Предел текучести s т, МПа	Предел прочности s в, МПа	Относительное удлинение e, %	Относительное сужение y, %
Ст0	-	-	³310	-	-
Ст1	-	-	310–500	-	-
Ст2	-	³200	330–420	-	-
Ст3	-	³220	370–470	-	-
Ст4	-	³240	410–520	-	-
Ст5	-	³270	500–640	-	-
Ст6	-	³300	³600	-	-
	Нормализация	³200	³330	³33	³60
	– ²–	³210	³340	³31	³55
	– ²–	³230	³380	³27	³55
	– ²–	³250	³420	³25	³55
	– ²–	³280	³460	³23	³50
	– ²–	³300	³500	³21	³50
	– ²–	³320	³540	³20	³45
	– ²–	³340	³580	³19	³45
	– ²–	³360	³610	³16	³40
	– ²–	³380	³640	³14	³40

• Лекция 1 . Перемещения при изгибе. Основные допущения. Дифференциальные уравнения изогнутой оси балки и его интегрирование.

• Лекция 2 . Метод начальных параметров. Универсальные формулы для определения прогибов и углов поворота поперечных сечений.

• Лекция 3 . Принцип возможных перемещений и его использование при расчете деформируемых систем. Формула Максвелла-Мора.

• Лекция 4 . Способы вычисления интеграла Мора: непосредственное интегрирование, способ Верещагина, формулы трапеций и Симпсона.

• Лекция 5 . Основы расчета статически неопределимых балок по методу сил. Степень статической неопределимости, основная система, уравнения совместности деформаций.

• Лекция 6. Сложное сопротивление. Построение эпюр внутренних усилий в пространственном ломанном стержне.

• Лекция 7. Одновременное действие продольной силы и изгибающих моментов. Определение нормальных напряжений и положения нулевой линии. Косой изгиб.

• Лекция 8. Внецентренное действие силы. Понятие о ядре сечения. Изгиб с кручением. Определение перемещений в пространственном стержне.

• Лекция 9. Общие понятия о теориях прочности. Критерий разрушения путем отрыва (хрупкое разрушение). Краткие сведения от первой и второй теориях прочности. Теория прочности Мора.

• Лекция 10. Критерий пластического состояния. Третья и четвертая теории прочности. Оценка прочности с применением теорий прочности. Понятия о новых теориях прочности и механики разрушения.

Перемещения при изгибе – dz dφ v = v (z ). Эта кривая называется упругой линией или линией прогибов .

Перемещения при изгибе – При изгибе ось балки искривляется (прогибается) в результате деформаций каждого элемента балки длиной dz , при которых смежные сечения поворачиваются относительно друг друга на угол dφ . При поперечном изгибе элемент испытывает дополнительные сдвиговые деформации, также изменяющие положение центра тяжести сечения относительно исходной осевой линии. В общем случае ось балки искривляется по кривой с уравнением v = v (z ). Эта кривая называется упругой линией или линией прогибов .

• Основные допущения –

• Прогибы малы.

• Влияние деформаций сдвига на величину прогиба пренебрежимо мало.

• При прогибе балки центр тяжести поперечного сечения перемещается перпендикулярно первоначальной оси балки в направлении главной оси сечения (y ).

• Поскольку влиянием деформаций сдвига пренебрегается, то каждое сечение согласно гипотезе плоских сечений при изгибе остается нормальным к оси изогнутого стержня (упругой линии). Отсюда угол наклона  сечения равен углу наклона θ касательной к упругой оси.

Метод начальных параметров – m m

Метод начальных параметров – Предыдущий пример показывает, что при двух участках приходится находить 4 константы интегрирования. Соответственно, при m участков число констант интегрирования равен 2m . С помощью специального выбора системы отсчета и использования некоторых приемов интегрирования можно добиться того, чтобы количество констант, подлежащих определению, оставалось равным двум при любом числе участков:

• Рассмотрим два соседних участка i и i +1, на границе между которыми приложен некоторый сосредоточенный силовой фактор, например, сила F. Начало координат общее для всех участков и совпадает с левым концом балки.

Лекция 2 (продолжение – 2.2)

• Таким образом получено у н и в е р с а л ь н о е уравнение упругой линии (прогибов) балки, называемое также, как

• уравнение метода начальных параметров:

• (запись слагаемых в порядке увеличения степени координаты

• и использование факториалов придает особенную изысканность

• и красоту или, лучше сказать, простоту)

• Принцип возможных перемещений – Для равновесия механической системы, подчиненной голономным (интегрируемым), стационарным, идеальным и двухсторонним связям, необходимо и достаточно, чтобы

• сумма элементарных работ всех приложенных активных сил на любом

• возможном перемещении из предполагаемого положения равновесия равнялось нулю :

• Способы вычисления интеграла Мора – Интеграл Мора, в котором подинтегральное выражение есть произведение двух функций, может быть вычислен различными методами в зависимости от вида этих функций. Заметим, одна из них, связанная с эпюрой внутренних усилий от единичного сосредоточенного воздействия, всегда линейная.

• 1. Непосредственное интегрирование – практически не имеет ограничений по использованию.

• 2. Способ Верещагина – удобен на тех участках, на которых легко можно определить центр тяжести одной из эпюр (обычно это относится к эпюре от грузового воздействия).

• 3. Формула Симпсона – применима в случае квадратичного закона изменения эпюры от грузового воздействия Формула трапеций – применяется в случае линейности обоих эпюр.

• 4. Формула трапеций – применяется в случае линейности обоих эпюр.

• ■ Основы расчета статически неопределимых систем методом сил – Напомним, что статически неопределимыми системами

• называются такие системы, в которых число неизвестных усилий (опорных реакций) превышает число независимых уравнений равновесия ,

• которые можно составить для рассматриваемой системы. Это означает, что статически неопределимая система имеет дополнительные связи ,

• которые с точки зрения обеспечения неизменяемости системы, рассматриваемой как совокупность абсолютно твердых (недеформируемых) тел,

• являются лишними .

Лекция 5 (продолжение – 5.2)

• ■ Система канонических уравнений метода сил – Уравнения деформаций могут быть записаны более подробно с выделением слагаемых от

• действия неизвестных сил и нагрузки:

Лекция 5 (продолжение – 5.3)

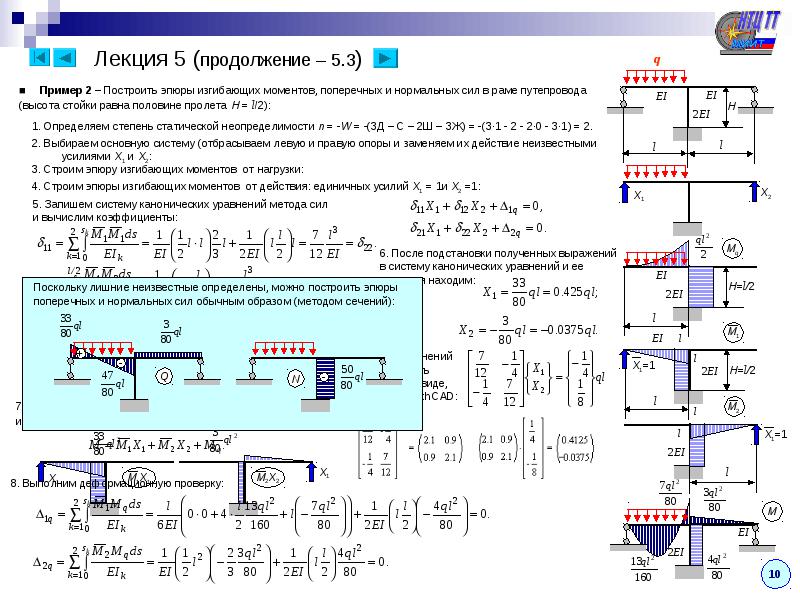
• ■ Пример 2 – Построить эпюры изгибающих моментов, поперечных и нормальных сил в раме путепровода

• (высота стойки равна половине пролета H = l /2):

■ Сложное сопротивление – N , Qx , Qy , Mx , My , Mz

■ Сложное сопротивление – Рассмотренные ранее случаи сопротивления прямого стержня, когда в сечении возникает лишь один вид внутреннего усилия, относятся к простым деформациям стержня: осевое растяжение-сжатие, чистый сдвиг, чистый (плоский) изгиб, чистое кручение. В реальных конструкциях стержни могут подвергаться более сложным видам сопротивления, представляющих собой сочетание нескольких простых деформаций, происходящих одновременно. Таким образом, возможно появление в поперечном сечении различных комбинаций ненулевых компонент из шести внутренних усилий: N , Qx , Qy , Mx , My , Mz . Такие комбинации, например, возникают в поперечных сечениях пространственного ломаного стержня (рычаги сложной конфигурации, коленчатые валы и т.п.) даже при нагрузке, лежащей в одной плоскости.

Лекция 6 (продолжение – 6.2)

• ■ Построение эпюр внутренних сил – Выполняется методом сечений так же, как и ранее:

• 1. Отбрасываются связи, заменяется их действие реакциями:

• Для статически определимого пространственного стержня число связей (и реакций) равно 6. В данном примере жесткая пространственная заделка

• должна быть заменена 3 реактивными силами RAx,RAy,RAz и 3 реактивными опорными моментами MAx, MAy , MAz :

• ■ Одновременное действие продольной силы и изгибающих моментов – Такая комбинация внутренних усилий характерна тем, что в поперечном сечении возникают нормальные напряжения, которые могут вычисляться по отдельности и складываться в соответствии с принципом независимости действия сил:

Лекция 7 (продолжение – 7.2)

• ■ Косой изгиб – В частном случае, при отсутствии продольной силы (N =0) и одновременном действии изгибающих моментов Mx и My сочетание двух прямых (плоских) изгибов вызывает косой изгиб .

• Нормальные напряжения в произвольной точке сечения теперь определяется выражением:

Лекция 8

■ Внецентренное растяжение-сжатие – Рассмотренная комбинация внутренних усилий может возникать при действии растягивающей или сжимающей силы F , не совпадающей с осью стержня и имеющей некоторые смещения относительно центральных осей (эксцентриситеты) xF и yF . При переносе силы параллельно самой себе в новый центр возникают моменты Mx и My присоединенных пар (метод Пуансо):

Лекция 8 (продолжение – 8.2)

• ■ Изгиб с кручением – При одновременном действии изгибающих моментов Mx и My и крутящего момента Mz в поперечном сечении возникают как нормальные напряжения (от изгиба), так и касательные напряжения (от кручения). Такое совместное действие испытывают оси редукторов, валы двигателей, ведущие оси колесных пар локомотивов.

• ■ Для определения опасного сечения в таких элементах должны быть построены эпюры указанных внутренних усилий, включая в определенных случаях эпюры поперечных сил.

■ В случае равенства моментов инерции относительно главных осей, что и имеет место для валов круглого сечения, при действии изгибающих моментов в двух плоскостях косой изгиб не возникает . Изгибающие моменты Mx и My могут быть заменены одним (полным) изгибающим моментом M и. Аналогично и поперечные силы Qy и Qx приводятся к равнодействующей силе Q . Таким образом, брус круглого сечения испытывает сочетание прямого (плоского) поперечного изгиба и кручения (при отсутствии продольной силы).

Лекция 8 (продолжение – 8.3)

• ■ Определение перемещений в пространственном стержне – В пространственном стержне в общем случае на каждом из участков могут возникать различные комбинации внутренних усилий. Техника построения эпюр для пространственных ломаных стержней рассматривалась в лекции 6.

Каждая точка оси бруса под действием приложенной нагрузки может иметь в общем случае три перемещения в пространстве (u, v и w). Кроме того, поперечное сечения бруса может иметь три угла поворота относительно центральных осей. Таким образом, необходим общий метод определения указанных перемещений. Таким методом является метод Максвелла-Мора, основанный на использовании вспомогательных состояний, в которых задается единичное усилие (сила или момент-пара сил) по направлению искомого перемещения.

• В самой общей форме перемещения с использованием интегралов Мора имеет вид:

Ранее было установлено дифференциальное уравнение изгиба (уравнение (237)), которое запишем в следующей форме:

После интегрирования уравнения (237) или (252) были получены значения прогиба и угла поворота (соотношения (238) и (239)). Одиако во многих случаях более удобно определить в результате интегрирования все основные параметры задачи: прогибы, углы поворота, изгибающие хмоменты и перерезывающие силы. Для эгого следует перейти к другой, эквивалентной форме дифференциального уравнения изгиба.

Дифференцируя равенство (252) по z и используя уравнение равновесия (82), получим

Рис. 8.67. Виды закрепления конца стержня: а - заделка; б - шарнирное закрепление; в - свободный конец; г - загруженный конец

Снова повторяя дифференцирование и ссылаясь на соотношение (81), приходим к следующему дифференциальному уравнению:

Это и есть основная форма дифференциального уравнения плоского изгиба стержня.

Для стержня постоянного сечения уравнение (254) будет таким:

Дифференциальное уравнение определяет широкий класс функций.

Из него должна быть выбрана функция, удовлетворяющая краевым условиям задачи (т. е. условиям закрепления концов стержня). Разберем эти условия при (рис. 8.67); при они имеют точно такой же вид.

Конец заделан:

Шарнирное закрепление:

Свободный конец:

Загруженный конец:

Если производная ограничена при то второе условие для свободного конца может быть принято в более простом виде:

Условия на загруженном конце согласованы с правилами знаков для и условиями (252) и (253) (рис. 8.3).

Уравнение (254) представляет дифференциальное уравнение четвертого порядка, и для однозначности решения должны быть заданы четыре краевых условия (по двана каждом конце). При наличии сосредоточенных моментов и сил должны быть заданы скачки производных в соответствующих сечениях.

Замечание. Уравнение (254) называется основным, так как объединяет основные уравнения изгиба: геометрические, физические и статические. Уравнение (252) включает уравнения равновесия только косвенно (при определении изгибающего момента).

В форме (254) уравнение изгиба используется в задачах колебания и устойчивости стержней и других задачах, где требуется более полный анализ. Уравнение изгиба в основной форме является разрешающим, т. е. позволяет по заданной функции найти основные параметры задачи без предварительного определения изгибающего момента в сечении.