Расчет ветровой нагрузки на стойку. Расчет деревянной стойки на сжатие. Общие положения

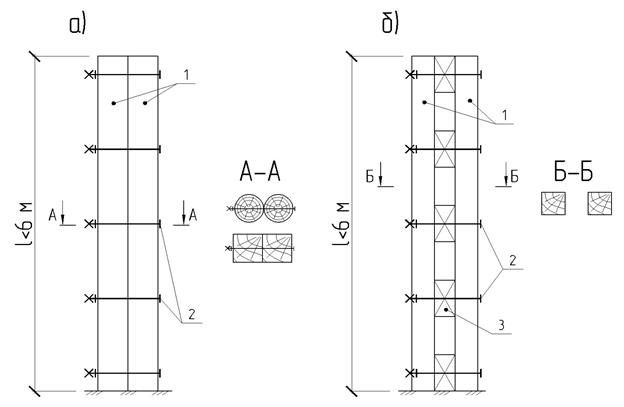
Элементами деревянных конструкций называют доски, бруски, брусья и бревна цельного сечения с размерами, указанными в сортаментах пилёных и круглых материалов. Они могут являться самостоятельными конструкциями, например, балками или стойками, а также стержнями более сложных конструкций.

Стойки из цельных элементов подразделяются на следующие виды:

1) в виде одиночного бруса или бревна

Такие стойки обладают сравнительно небольшой несущей способностью. Их высота и размер поперечного сечения ограничено сортаментом лесоматериалов. В этих стойках применяют обычно шарнирное опирание на фундамент.

2) Стойки в виде элементов составного сечения набранного из двух или нескольких брусьев, досок или бревен, соединенных болтами или другими податливыми связями

Стойки составного сечения так же имеют высоту, ограниченную сортаментом, однако, их несущая способность может быть существенно выше по сравнению со стойками из одиночного сечения.

Соединения, применяемые для сплачивания этих стоек (болты, гвозди, шпонки) являются податливыми, что увеличивает гибкость стоек и должно быть учтено при расчете

На сжатие работают стойки, подкосы, верхние пояса и некоторые стержни ферм. Пороки меньше снижают прочность древесины, чем при растяжении, поэтому расчетное сопротивление реальной древесины при сжатии выше и составляет для древесины 1 сорта R с = 14÷16 МПа.

Усилия в элементах определяют общими методами строительной механики. Проверка прочности элемента заключается в определении напряжений в сечениях, которые не должны превышать расчетных сопротивлений древесины, установленных нормами проектирования. Деревянные элементы рассчитывают в соответствии со СНиП II-25-80.

В этом СНиП ряд обозначений не соответствует принятым в других нормах. Так площадь обозначается F, радиус инерции – r .

Расчет на прочность сжатых элементов производится по формуле:

σ = N / F нетто ≤ R c ,

где R с – расчетное сопротивление сжатию.

Сжатые стержни, имеющие большую длину и не закрепленные в поперечном направлении должны быть, помимо расчета на прочность, рассчитаны на продольный изгиб. Явление продольного изгиба заключается в том, что гибкий центрально-сжатый прямой стержень теряет свою прямолинейную форму (теряет устойчивость) и начинает выпучиваться при напряжениях, значительно меньших предела прочности. Проверку сжатого элемента с учетом его устойчивости производят по формуле:

σ = N / φ F расч ,

где – расчетная площадь поперечного сечения,

φ – коэффициент продольного изгиба.

Принимается равной:

1. При отсутствии ослаблений = ,

2. При ослаблениях, не выходящих на кромки (а), если площадь ослаблений не превышает 25% , = ,

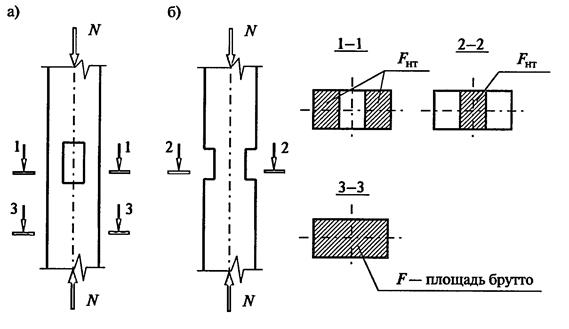
3. То же, если площадь ослаблений превышает 25% , =4/3 ,

4. При симметричных ослаблениях, выходящих на кромки (б) = ,

В случае наличия ослаблений (отверстий под болты, врезки для прикрепления подкосов, связей) кроме расчета на устойчивость, обязателен расчет на прочность

σ = N / F нетто ≤ R c , кн/см 2 .

Коэффициент продольного изгиба φ всегда меньше 1, учитывает влияние устойчивости на снижение несущей способности сжатого элемента в зависимости от его расчетной максимальной гибкости λ .

Гибкость элемента равна отношению расчетной длины l 0 к радиусу инерции сечения элемента:

r = √I бр / F бр, см

Расчетную длину элемента l 0 следует определять умножением его свободной длины l на коэффициент μ 0:

l 0 =l μ 0 ,

где коэффициент μ 0 принимается в зависимости от типа закрепления концов элемента:

При шарнирно закрепленных концах μ 0 =1;

При одном шарнирно закрепленном, а другом защемленном μ 0 =0,8;

При одном защемленном, а другом свободном нагруженном конце μ 0 =2,2;

При обоих защемленных концах μ 0 =0,65.

Гибкость сжатых элементов ограничивается с тем, чтобы они не получились недопустимо гибкими и недостаточно надежными. Отдельные элементы конструкций (отдельные стойки, пояса, опорные раскосы ферм и т.п.) должны иметь гибкость не более 120. Прочие сжатые элементы основных конструкций – не более 150, элементы связей – 200.

При гибкости более 70 (λ >70) сжатый элемент теряет устойчивость, когда напряжения сжатия в древесине еще невелики и она работает упруго.

При гибкостях, равных и меньших 70 (λ ≤70) элемент теряет устойчивость, когда напряжения сжатия достигают упругопластической стадии и φ = 1 – 0,8(λ /100) 2

Общий порядок расчета деревянных стоек при подборе поперечного сечения:

1. Определяют нагрузку

2. Устанавливают расчетную схему стойки

3. Определяют расчетную длину стойки l 0 =l μ 0

4. Принимают породу древесины и её сорт

5. Определяют расчетное сопротивление древесины на сжатие

6. Задаются коэффициентом продольного изгиба φ= 0,6 ÷0,7

7. Определяется требуемая площадь сечения стойки

F расч ≥ N / φR y

8. По найденной площади назначают размеры поперечного сечения:

· Для квадратного сечения

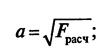
· Для круглого сечения

Полученные размеры округляют в большую сторону с учетом сортамента пиломатериалов

9. Определяют радиусы инерции

10. Находят гибкость и проверяют условия, ограничивающие гибкость

λ пред = 120 для стоек, если условие не удовлетворено, то размеры сечения увеличивают и снова поверяют гибкость.

11. Проверяют устойчивость принятого сечения для этого:

· Определяют фактическое значение расчетной площади F расч

· Определяют коэффициент продольного изгиба φ

· Находят напряжения и сравнивают с расчетным сопротивлением σ = N /φ F расч ≤ R c , кн/см 2 .

12. Если есть ослабления, проверяют прочность деревянной стойки

σ = N / F нетто ≤ R c , кн/см 2 .

13. Если устойчивость или прочность стойки не обеспечена, то увеличивают размеры сечения и снова проводят проверку на устойчивость или прочность.

Литература: В.И. Сетков «Строительные конструкции»,М.,

ИНФРА-М,2009, с. 107-112

На практике часто возникает необходимость расчета стойки или колони на максимальную осевую (продольную) нагрузку. Усилие, при котором стойка теряет устойчивое состояние (несущую способность) является критическим. На устойчивость стойки оказывает влияние способ закрепления концов стойки. В строительной механике рассматривают семь способов закрепления концов стойки. Ми рассмотрим три основных способа:

Для обеспечения определенного запаса устойчивости необходимо чтобы соблюдалось условие:

Где: Р - действующее усилие;

Устанавливается определенный коэффициент запаса устойчивости

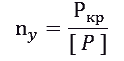
Таким образом, при расчете упругих систем необходимо уметь определять величину критической силы Ркр. Если иметь введу что усилие Р приложено к стойке вызывает только малые отклонения от прямолинейной формы стойки длиной ι то его можно определить из уравнения

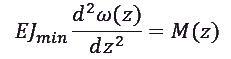
где: E - модуль упругости;
J_min- минимальный момент инерции сечения;
M(z) - изгибающий момент, равный M(z) = -P ω;
ω - величина отклонения от прямолинейной формы стойки;
Решая это дифференциальное уравнение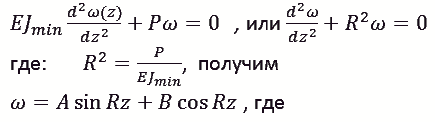

А и В постоянные интегрирования, определяются по граничным условиям.
Произведя определенные действия и подстановки получим конечное выражение для критической силы Р

Наименьшее значение критической силы будет при n = 1 (целое число) и

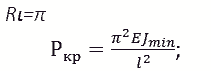
Уравнение упругой линии стойки будет иметь вид:

где: z - текущая ордината, при максимальном значении z=l;
Допустимое выражение для критической силы называется формулой Л.Эйлера. Видно, что величина критической силы зависит от жесткости стойки EJ min прямо пропорционально и от длины стойки l - обратно пропорционально.
Как было сказано, устойчивость упругой стойки зависит от способа ее закрепления.
Рекомендуемая величина запаса прочности для стальных стоек ровна
n y =1,5÷3,0; для деревянных n y =2,5÷3,5 ; для чугунных n y =4,5÷5,5
Для учета способа закрепления концов стойки вводиться коэффициент концов приведенной гибкости стойки.

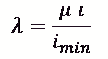
где: μ - коэффициент приведенной длины (Таблица) ;
i min - наименьший радиус инерции поперечного сечения стойки (таблица);
ι - длина стойки;
Вводиться коэффициент критической нагрузки:

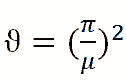
, (таблица);
Таким образом, при расчете поперечного сечения стойки необходимо учитывать коэффициенты μ и ϑ величина которых зависит от способа закрепления концов стойки и приведена в таблицах справочника по сопромату (Г.С. Писаренко и С.П.Фесик)
Приведем пример расчета критической силы для стержня сплошного сечения прямоугольной формы - 6×1 см., длина стержня ι = 2м. Закрепления концов по схеме III.
Расчет:
По таблице находим коэффициент ϑ=9,97, μ = 1. Момент инерции сечения будет:

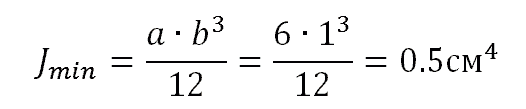
а критическое напряжение будет:

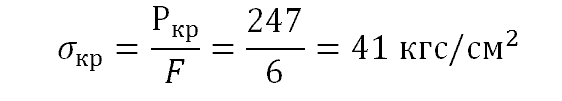
Очевидно, что критическая сила Р кр =247 кгс вызовет в стержне напряжение всего 41кгс/см 2 , что значительно меньше предела проточности (1600кгс/см 2), однако эта сила вызовет искривление стержня, а значит потерю устойчивости.
Рассмотрим другой пример расчета деревянной стойки круглого сечения защемленной в нижнем конце и шарнирно закрепленной на верхнем (С.П. Фесик) . Длина стойки 4м, сила сжатия N=6тс. Допускаемое напряжение [σ]=100кгс/см 2 . Принимаем коэффициент понижения допускаемого напряжения на сжатие φ=0.5. Вычисляем площадь сечения стойки:

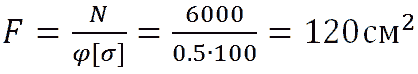
Определяем диаметр стойки: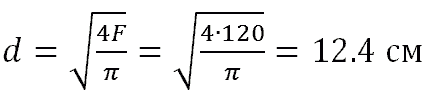

Момент инерции сечения

Вычисляем гибкость стойки: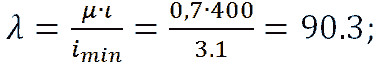
где: μ=0.7, исходя из способа защемления концов стойки;
Определяем напряжение в стойке: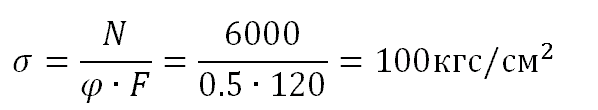

Очевидно, что напряжение в стойке составляет 100кгс/см 2 и оно ровно допустимому напряжению [σ]=100кгс/см 2
Рассмотрим третий пример расчета стальной стойки из двутаврового профиля, длиной 1.5м, сила сжатия 50тс, допускаемое напряжение [σ]=1600кгс/см 2 . Нижний конец стойки защемлен, а верхний свободный (I способ).
Для подбора сечения используем формулу и задаемся коэффициентом ϕ=0.5, тогда:

Подбираем из сортамента двутавр №36 и его данные: F=61.9см 2 , i min =2.89см.
Определяем гибкость стойки:

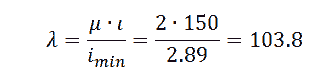
где: μ из таблицы, ровное 2, учитывая способ защемления стойки;
Расчетное напряжение в стойке будет: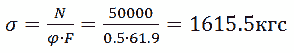

5кгс,что примерно ровно допустимому напряжению, и на 0.97% больше, что допустимо в инженерных расчетах.
Поперечное сечение стержней работающих на сжатие будет рациональным при наибольшем радиусе инерции. При расчете удельного радиуса инерции
наиболее оптимальным является трубчатые сечения, тонкостенные; для которых величина ξ=1÷2.25, а для сплошных или прокатных профилей ξ=0.204÷0.5

Выводы
При расчете на прочность и устойчивость стоек, колон необходимо учитывать способ закрепления концов стоек, применять рекомендуемый запас прочности.
Значение критической силы получено из дифференциального уравнения изогнутой осевой линии стойки (Л.Эйлера).
Для учета всех факторов, характеризующих нагруженную стойку введено понятие гибкости стойки - λ, коэффициент провиденной длины - μ, коэффициент понижения напряжения - ϕ, коэффициент критической нагрузки - ϑ. Их значения берут из таблиц справочников (Г.С.Писарентко и С.П.Фесик).
Приведены примерные расчеты стоек, на определение критической силы - Ркр, критического напряжения - σкр, диаметра стоек - d, гибкости стоек - λ и другие характеристики.
Оптимальным сечением для стоек и колон является трубчатые тонкостенные профиля с одинаковыми главными моментами инерции.

Используемая литература:
Г.С Писаренко «Справочник по сопротивлению материалов».
С.П.Фесик «Справочник по сопротивлению материалов».
В.И. Анурьев «Справочник конструктора-машиностроителя».
СНиП II-6-74 «Нагрузки и воздействия, нормы проектирования».

Отличие колонн, стоек или подкосов от балок в том, что колонны, стойки и подкосы работают как правило только на сжатие, в то время как балки должны стойко сопротивляться изгибающему моменту, хотя и сжатие при этом также могут испытывать. С точки зрения строительной механики не имеет значения, из какого материала изготовлен элемент, работающий на сжатие, из металла, железобетона, пластика, стекла или древесины. Любой такой элемент, назовем его стержнем, должен выдерживать прикладываемую к нему нагрузку:

σ = N/F ≤ R с (1.1)

где σ - внутренние нормальные напряжения, возникающие в поперечном сечении сжимаемого элемента, кг/см 2 ;

F - площадь поперечного сечения колонны, стойки или любого другого элемента, работающего на сжатие, см 2 ;

R с - расчетное сопротивление древесины сжатию по пределу текучести, кг/см 2 . Для сосны первого сорта относительно небольшого сечения расчетное сопротивление составляет 140 кгс/см 2 . Чем ниже сорт, тем меньше расчетное сопротивление. При сечениях элемента более 11х11 см, а также для других пород древесины расчетное сопротивление можно определить по соответствующей таблице .

Суть данной формулы проста -

внутренние нормальные напряжения возникающие в сжимаемых элементах, должны быть меньше или равны расчетному сопротивлению. Это обеспечивает необходимую прочность элемента

Таким образом расчет на прочность по формуле (1.1) можно отнести к расчету по первой группе предельных состояний.

Как видим, по уровню сложности задача относится ко второму, максимум к третьему классу общеобразовательной школы. Однако с точки зрения теории сопротивления материалов все далеко не так просто по ряду причин:

1. Древесина - неоднородный природный материал, к тому же анизотропный. На несущую способность деревянных элементов влияют сучки, трещины, влажность и множество других факторов. В частности влияние размеров сечения учитывается, как мы уже видели разным значением расчетного сопротивления, чем меньше размеры сечения, тем больше влияние возможных дефектов древесины на несущую способность и потому для таких элементов расчетное сопротивление меньше.

2. Формула (1.1) предполагает, что сосредоточенная нагрузка N прикладывается точно к центру тяжести О поперечного сечения сжимаемого элемента. В действительности нагрузка практически всегда будет распределенной, причем далеко не всегда равномерно распределенной, так как идеально выдержать геометрические размеры деревянных элементов конструкции - нереально. Если торец (опорная площадка) колонны или стройки получен в результате распила ручной пилой по дереву - это одно, а если циркулярной пилой, то это совсем другое. В первом случае из-за возможных отклонений в перпендикулярности распила, а также в зависимости от размера зубьев пилы, нагрузка на колонну или стойку будет передаваться не по всей площади сечения, а только там где древесина различных элементов контактирует между собой. Помимо уменьшения площади контакта это также приводит и к появлению эксцентриситета приложения нагрузки. А если есть эксцентриситет, то есть и продольный изгибающий момент, действующий в поперечном сечении колонны или стойки.

3. С точки зрения строительной механики рассчитываемые элементы в данном случае прямолинейны, это означает что все центры тяжести О поперечных сечений рассчитываемых элементов расположены на одной прямой - центральной оси. Но древесина - неоднородный материал, имеющий разную плотность в зависимости от процентного содержания сердцевины, ядра и заболони в поперечном сечении, а кроме того, в результате сушки пиломатериалы часто изменяют свою форму, проще говоря, выгибаются, иногда так, что вообще использование сильно поведенных элементов ставится под вопрос. А это означает, что центры тяжести поперечных сечений по длине колонны или стойки будут смещены относительно центральной оси, что опять же можно рассматривать как эксцентриситет приложения нагрузки.

4. Под действием приложенной нагрузки колонна или стойка очень редко равномерно сжимается подобно пружине по вышеуказанным причинам, но очень часто выгибается в ту или иную сторону, напоминая при этом обычную балку, и такое поведение деревянных элементов следует учитывать при расчетах.

Конечно же, учесть все вышеуказанные отклонения и дефекты для стоек, колон или подкосов, которые в процессе проектирования существуют только на бумаге или в голове проектировщика - нереально. А вот добавить в формулу (1.1) некий поправочный коэффициент, максимально учитывающий вышеизложенные факторы - реально вполне. Таким коэффициентом является коэффициент продольного изгиба φ :

σ = N/φF ≤ R c (1.2)

Таким образом мы получили формулу для проверки сжимаемых элементов на устойчивость .

Значение коэффициента продольного изгиба φ зависит от гибкости сжимаемого элемента λ . А гибкость элемента в свою очередь зависит от соотношения длины сжимаемого элемента к радиусу инерции поперечного сечения. Физический смысл понятия гибкость сжимаемого элемента приблизительно следующий:

чем больше длина сжимаемого элемента и чем меньше при этом высота и ширина рассчитываемого поперечного сечения элемента, тем больше вероятность того, что действующая на колонну, стойку или подкос нагрузка будет вызывать не равномерное сжатие, но еще и смещение центра тяжести относительно оси х

проще говоря продольный изгиб, а это значит, что сжимающие напряжения в различных точках поперечного сечения будут неодинаковыми.

Например, куб (рисунок 250.1. а) при действии некоторой равномерно распределенной нагрузки по всему сечению будет деформироваться (сжиматься) достаточно равномерно, соответственно гибкость куба будет близка к 0 и потому значение коэффициента продольного изгиба будет близко к 1. Согнуть куб практически не возможно. А если это будет не куб, а стойка квадратного сечения (рисунок 250.1. б), имеющая точно такие же размеры поперечного сечения, то чем больше будет длина стойки, тем больше будет гибкость стойки и значит вероятность того, что стойка не просто сожмется, а еще и выгнется, будет выше. Например, металлический пруток квадратного сечения имеет достаточно большую расчетную прочность и при сечении 2х2 см может выдерживать нагрузки на растяжение до 8-10 тонн (в зависимости от класса стали) вне зависимости от длины. В то же время чем больше будет длина прутка, тем меньше будет прикладываемая нагрузка, при которой центр тяжести поперечного сечения прутка посредине длины начнет смещаться относительно оси y или z , увеличивая таким образом величину эксцентриситета для данного сечения, а чем больше эксцентриситет, тем больше будут нормальные напряжения в этом поперечном сечении, и в итоге пруток согнется (потеряет устойчивость). При достаточно большой длине это может произойти даже под действием собственного веса. А стойка прямоугольного сечения (рисунок 250.1. в) скорее всего выгнется относительно той оси, относительно которой прочностные характеристики стойки меньше:

Рисунок 250.1 . Эпюры внутренних напряжений в поперечных сечениях элементов с различными геометрическими параметрами.

На рисунке 250.1 достаточно условно (для большей наглядности) показаны эпюры внутренних сжимающих напряжений σ относительно главных осей z и у , при действии одинаковой по значению распределенной нагрузки на стержни (стойки) из одного материала но с различными геометрическими параметрами. Если посмотреть на деформации, которые возникают в сжимаемых элементах под действием этой нагрузки, то мы увидим, что эпюры сжимающих напряжений очень похожи на величину деформации сжимаемых элементов и в этом нет ничего удивительного, так как эти самые деформации и возникают в результате действия сжимающих напряжений. Более подробно это рассматривалось в статье: "Основы сопромата. Расчет прогиба балки ", но сейчас нас интересует другое, а именно:

Так как на куб и два стержня действует одинаковая нагрузка, то и суммарное значение возникающих сжимающих напряжений для всех трех поперечных сечений одинаковое. Однако для куба эти напряжения равномерны (условно, неоднородность материала и прочие факторы конечно влияют, но будем считать влияние этих факторов незначительным), нет ни максимальных ни минимальных значений. В этом случае гибкость куба λ = 0 , а коэффициент продольного изгиба φ = 1 .

Для стержня (стойки) квадратного сечения по перечисленным выше причинам распределение сжимающих напряжений в плоскости поперечного сечения будет уже не таким равномерным. В результате даже небольшого продольного изгиба в поперечном сечении стойки будут возникать как сжимающие так и растягивающие напряжения , при этом эпюра сжимающих напряжений от действующей нагрузки будет точно такой же, как и для куба, однако суммарная эпюра будет выглядеть приблизительно так, как показано на рисунке 250.1. б. А это означает что максимальные сжимающие напряжения (на рисунке показаны красным цветом), возникающие ближе к граням сечения, будут больше среднего значения (показано синим цветом), которое используется при расчете на прочность.

Для стержня (стойки) прямоугольного сечения прогиб произойдет только вдоль оси z , так как момент сопротивления, да и момент инерции относительно оси у для такого сечения будет минимальным. При этом в поперечном сечении могут возникать не только сжимающие но и растягивающие напряжения, от чего это зависит мы узнаем чуть позже. А пока еще раз посмотрим на эпюры напряжений.

Если бы мы прикладывали к кубу и стержням максимально допустимые по несущей способности нагрузки, то очевидно, что для соблюдения условий формулы (1.1) максимальные значения сжимающих напряжений (обозначены красным цветом) должны быть одинаковыми для куба и двух стержней, а это означает, что среднее значение сжимающих напряжений (обозначено синим цветом) для стержня квадратного сечения будет меньше, чем для куба, а для стержня прямоугольного сечения еще меньше, чем для стержня квадратного сечения. Таким образом эти эпюры можно рассматривать как графическое отображение коэффициента продольного изгиба. Если бы эпюры были построены точно, то приблизительное значение коэффициента продольного изгиба для стержня квадратного сечения, показанного на рисунке 250.1. б) составило φ ≈ 0.75-0.8 . А для стержня прямоугольной формы, показанного на рисунке 250.1. в) φ ≈ 0.4-0.45 .

Однако картинки - картинками, но для расчета конструкций нужны более точные цифры. СНиП II-25-80(1988) предлагает следующие формулы для расчета коэффициента продольного изгиба в зависимости от значения гибкости:

При λ ≤ 70

φ = 1 - a(λ/100) 2 (1.3)

где коэффициент а = 0,8 - для древесины или а = 1 - для фанеры;

при λ > 70

φ = A/λ 2 (1.4)

где коэффициент А = 3000 - для древесины или А = 2500 - для фанеры.

Раньше для определения этого соотношения использовались таблицы или графики, в принципе ими можно пользоваться и сейчас, например полученные по графику 250.1 значения будут достаточно близкими к определенным по формулам:

250.2 График зависимости коэффициента продольного изгиба от гибкости.

Удобство данного графика еще и в том, что для определения гибкости необязательно сначала находить радиус инерции, а можно сразу определить коэффициент продольного изгиба по соотношению расчетной длины к высоте или ширине поперечного сечения или по отношению расчетной длины к диаметру, если рассчитываемый стержень имеет круглое сечение. Тем не менее знать, что же такое расчетная длина и почему она бывает разной и что такое радиус инерции, все-таки надо.

Математически гибкость элемента выражается так:

λ = l o /i или λ = l o /r u (1.5)

где l o - расчетная длина стойки (стержня, колонны, подкоса или любого другого сжимаемого элемента).

Расчетная и реальная длина колонны - разные понятия .

Расчетная длина сжимаемого элемента зависит от способа закрепления концов сжимаемого элемента. Варианты значений расчетной длины показаны на графике 250.1 справа. Почему расчетная длина при разных способах закрепления имеет различные значения описывается отдельно .

i или r u - радиус инерции сечения, еще его называют радиусом ядра сечения. Постараюсь объяснить, что такое радиус инерции, как можно более просто и кратко.

Понятие радиус инерции или радиус ядра сечения

полностью справедливо только для круглых сечений. У сечений круглой формы ядро сечения действительно представляет собой круг (рис.250.3. а), у сечений сложной геометрической формы ядро сечения как правило представляет собой эллипс (рис.250.3. г), а у сечений прямоугольной формы ядро сечения представляет собой ромб (рис.250.3. в) или квадрат - для сечений квадратной формы (рис.250.3. б):

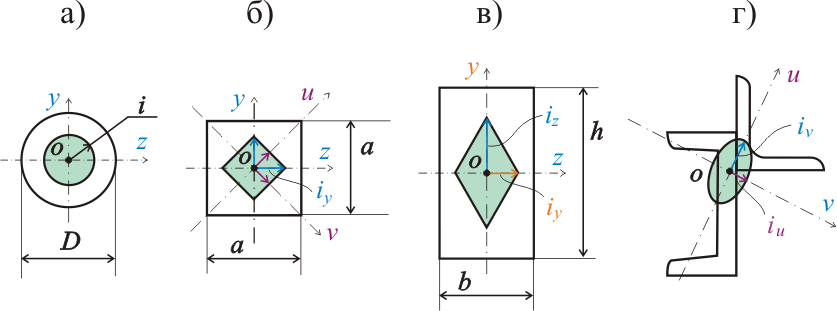
Рисунок 250.3. Ядра сечения и радиусы инерции для сечений различных геометрических форм.

Физический смысл ядра сечения следующий

нагрузка к сжимаемому элементу далеко не всегда прикладывается к центру тяжести поперечного сечения. На рисунке 250.1 показана равномерно распределенная нагрузка, равнодействующая которой приложена именно к центру тяжести О . Но если бы к кубу (рис.250.1 а) была приложена неравномерно распределенная нагрузка или некая сосредоточенная нагрузка N , то суммарная эпюра сжимающих напряжений зависела бы от точки приложения сосредоточенной нагрузки или равнодействующей неравномерно распределенной нагрузки. Если бы сосредоточенная нагрузка прикладывалась относительно недалеко от центра тяжести поперечного сечения, то эпюра сжимающих напряжений выглядела бы, как на рис.250.1 б. А при значительном значении эксцентриситета приложения нагрузки эпюра сжимающих напряжений выглядела бы как на рис.250.1. в), т.е. в поперечном сечении действовали не только сжимающие, но и растягивающие напряжения. А при некотором (не показанном на рисунке 250.1) значении эксцентриситета эпюра сжимающих напряжений представляла бы собой треугольник.

Так вот, радиус ядра сечения - это и есть эксцентриситет, при котором эпюра напряжений представляет собой треугольник

Таким образом радиус ядра круглого сечения - это действительно радиус некоей окружности, на которой расположены эксцентриситеты нагрузки, при которых эпюра сжимающих напряжений представляет собой треугольник. И получается, что если сосредоточенная нагрузка или равнодействующая неравномерно распределенной нагрузки будет приложена в любой точке внутри этой окружности, то в поперечном сечении будут действовать только сжимающие напряжения.

Область внутри окружности, описываемой радиусом инерции, называется ядром сечения

На рисунке 250.3 ядра сечений обозначены зеленым цветом, для наглядности размеры ядер изменены.

Понятие ядра настолько универсально, что его используют даже такие далекие от сопромата люди, как seo-оптимизаторы, обильно насыщающие свою речь выражениями типа: составление семантического ядра, или анализ семантического ядра. На seo-слэнге под семантическим ядром подразумевается набор ключевых слов сайта и эти ключевые слова должны подбираться, а затем и использоваться так, чтобы реакция поисковиков была только положительной. Все остальные слова - это просто текст. Но не будем отвлекаться и вернемся к радиусу ядра сечения. Почему радиус ядра сечения называется также радиусом инерции? Оказывается, если умножить площадь поперечного сечения на квадрат радиуса ядра сечения, то мы получим момент инерции.