Напряжение сдвига это. Какие напряжения возникают в поперечных сечениях стержня при сдвиге

Касательное напряжение — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы касательное напряжение EN shear stress …

У этого термина существуют и другие значения, см. Напряжение. Напряжённому состоянию чистого сдвига, при котором по двум взаимно перпендикулярным площадкам действуют только касательные напряжения, соответствует модуль сдвига. Модуль сдвига… … Википедия

напряжение сдвига - 2.1.5 напряжение сдвига: Отношение движущей силы к единице площади потока жидкости. Для ротационного вискозиметра поверхность ротора является площадью сдвига. Крутящий момент, приложенный к ротору, Тr, Н×м, вычисляют по формуле Тr = 9,81m(R0 +… …

напряжение сдвига, параллельное оси сварки - — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции EN shear stress parallel to weld axis … Справочник технического переводчика

напряжение сдвига, перпендикулярное оси сварки - — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции EN shear stress perpendicular to weld axis … Справочник технического переводчика

предельное напряжение сдвига - — Тематики нефтегазовая промышленность EN yield strength … Справочник технического переводчика

Напряжение: В Викисловаре есть статья «напряжение» Электрическое напряжение между точками A и B отношение работы электрического поля при переносе пробного заряда из точки A в B к величине этого пробного заряда. Номинальное напряжение… … Википедия

напряжение - 3.10 напряжение: Отношение растягивающего усилия к площади поперечного сечения звена при его номинальных размерах. Источник: ГОСТ 30188 97: Цепи грузоподъемные калиброванные высокопрочные. Технические условия … Словарь-справочник терминов нормативно-технической документации

НАПРЯЖЕНИЕ МЕХАНИЧЕСКОЕ, сила на единицу площади, прилагаемая к объекту. Различают напряжение растяжения, сжатия и сдвига (деформирующее объект в направлениях по касательной). В текучих средах напряжение по касательной невозможно, так как этим… … Научно-технический энциклопедический словарь

переходное восстанавливающееся напряжение - 3.63 переходное восстанавливающееся напряжение; ПВН: Восстанавливающееся напряжение в период времени, когда оно имеет заметно выраженный переходный характер. Примечания 1 Переходное восстанавливающееся напряжение может быть колебательным или… … Словарь-справочник терминов нормативно-технической документации

Сдвиг элементов конструкций. Определение внутренних усилий, напряжений и деформаций при сдвиге. Понятие о чистом сдвиге. Закон Гука для сдвига. Удельная потенциальная энергия деформации при чистом сдвиге. Расчеты на прочность.

8. ПРОСТЫЕ ВИДЫ СОПРОТИВЛЕНИЯ. СДВИГ

8.1. Определение внутренних усилий при сдвиге

Кроме деформации растяжения или сжатия (см. лекцию № 3) материал нагруженного элемента конструкции может испытывать деформацию сдвига.

Сдвиг – вид сопротивления, при котором стержень нагружен двумя равными силами (на малом расстоянии друг от друга), перпендикулярными к оси бруса и направленными в противоположные стороны.

Примером такого действия сил на брус может быть разрезание ножницами прутьев, деформация заклепок, болтов, сварных швов между металлическими листами и т. п. Вообще же на практике сдвиг в чистом виде получить трудно, так как обычно деформация сдвига сопровождается другими видами деформаций и чаще всего изгибом.

Установим формулы для внутренних усилий, напряжений и деформаций, необходимые при расчете на сдвиг элементов конструкций, имеющих форму бруса. Пусть известна внешняя нагрузка F , вызывающая сдвиг одной части бруса относительно другой. Используя метод мысленных сечений (см. рисунок), находим величину внутренних усилий, действующих в сечении бруса. Очевидно, что в данном случае нагружения из шести уравнений равновесия лишь одно не обращается тождественно в ноль:

∑ Fy = 0 Qy = F.

Таким образом, при сдвиге из шести внутренних

усилий (N ,Q y ,Q z ,M x ,M y ,M z ) в сечении элемента конструкции возникают только одно – поперечная

сила (Q y илиQ z ).

8.2. Определение напряжений при сдвиге. Понятие о чистом сдвиге

Так как поперечная сила Q y (илиQ z ) является единственным внутренним усилием, возникающим в сечении стержня при сдвиге, и при этом она лежит в плоскости этого сечения, то и напряжения, возникающие здесь, должны лежать в плоскости сечения стержня. То есть при сдвиге в точках поперечного сечения стержня возникают только касательные напряженияτ .

В соответствии с определением (см. лекцию № 1), касательные напряжения τ , действующие в поперечном сечении (A ) бруса, представляют собой интенсивность внутренних поперечных сил

τ= dQ dA ,

исходя из чего можем записать (опуская соответствующие индексы):

Q = ∫ τ dA.

При сдвиге условно считают, что касательные напряжения равномерно рас-

пределены по площади поперечного сечения (τ =const ), поэтому

Q = τ A.

Тогда касательные напряжения при сдвиге определяются так:

					.	(8.1)

Рассмотрим характер напряженно-деформированного состояния, которое возникает в точках стержня при сдвиге.

По закону парности касательных напряжений в продольных сечениях бруса, так же как и в его поперечных сечениях будут возникать только касательные напряжения. Тогда на гранях (параллельных соответствующим осям координат) бесконечно малого элемента, «вырезанного» в окрестности любой точки стержня при сдвиге, будут действовать только касательные напряжения τ . Такой случай напряженного состояния называют чистым сдвигом.

Чистый сдвиг – частный случай плоского напряженного состояния, при котором по граням прямоугольного элемента действуют только касательные напряжения.

Определим величину и направление главных напряжений при чистом сдвиге:

	σ 1,3		σx +σy				(σ x−σ y) 2 + 4 τ 2 xy,

учитывая, что σ x =σ y =0,

tg2 α= −∞	2 α= −				π .

Как видим, при чистом сдвиге главные напряжения одинаковы по величине, противоположны по знаку (σ 1 =–σ 3 =τ xy ) и направлены под углом 45о к оси стержня (третья главная площадка элемента совпадает с ненагруженной фасадной гранью элемента, следовательноσ 2 =0).

8.3. Определение деформаций и закон Гука при чистом сдвиге

Рассмотрим деформацию квадратного элемента при чистом сдвиге (см. рисунок).

Поскольку по граням элемента не действуют нормальные напряжения, то вдоль граней нет и удлинений. В то же время диагональ, совпадающая с направлением σ 1 , удлинится, а другая диагональ, совпадающая с направлением сжимающего напряженияσ 3 , укоротится. В результате квадрат трансформируется в ромб без изменения длины граней. Таким образом, деформация чистого сдвига характеризуется изменением первоначально прямых углов.

Более наглядное представление о деформации элемента при сдвиге можно получить, закрепив одну из граней (см. рисунок).

Малый угол γ xy , на который изменяется первоначально прямой угол элемента

при сдвиге, называется углом сдвигаили относительным сдвигом:

γxy =BAB 1 .

Величину абсолютного смещения грани обозначают ∆ s и называютабсолют-

ным сдвигом.

Из треугольника BAB 1 следует, что

tgγ xy = ∆ a s .

Учитывая малость угла, можно считать, что

tg γ xy≈γ xy,

тогда окончательно запишем взаимосвязь между относительным и абсолютным сдвигом элемента

γ xy=	∆ s .

Зависимость между нагрузкой и деформацией при сдвиге можно проследить по так называемой диаграмме сдвига, которую получают обычно из опытов на кручение тонкостенных трубчатых образцов (в стенках которых, как увидим далее, также возникает напряженное состояние чистого сдвига). Для пластичных материалов диаграмма сдвига аналогична диаграмме растяжения и имеет с ней одинаковые характерные участки, в том числе и участок упругости.

Рассматривая деформацию сдвига в пределах упругости, найдем, что между углом сдвига γ xy и касательными напряжениямиτ xy существует линейная зависимость, которая носит названиезакона Гука при сдвиге и может быть выражена следующими формулами:

где G – коэффициент пропорциональности, который называется модулем упругости при сдвиге или модулем упругости второго рода и является константой для данного материала. Модуль сдвига может быть определен аналитически, если известны величины модуля Юнга и коэффициента Пуассона:

Заметим, что все рассмотренные характеристики упругости материала E ,µ ,G ,K взаимосвязаны, однако в сопротивлении материалов и в теории упругости только две из них (чаще всегоE иµ ) принимаются независимыми.

Подставляя выражения (8.1) и (8.2) в формулы (8.3), можно записать закон Гука при сдвиге и во «внешних формах» (через абсолютные деформации и внутренние усилия):

∆ s =G Q a A ,

где a – расстояние между сдвигаемыми гранями;A – площадь грани.

Как уже отмечалось во введении, при смещении одного поперечного сечения относительно другого возникают касательные напряжения.

Тогда, если в поперечном сечении стержня площадью F возникает перерезывающая сила , то касательные напряжения в любой точке этого сечения будут равны

Касательные напряжения измеряются в тех же единицах, что и нормальные напряжения : мегапаскалях, килоньютонах на квадратный сантиметр (МПа, кН/см 2), а также в килограммах силы на квадратный сантиметр или миллиметр (кгс/см 2 , кгс/мм 2).

3.4. Как записывается закон Гука при сдвиге? Что называется модулем сдвига и в каких единицах он измеряется?

Опытным путем установлено, что в пределах упругой сдвиговой деформации касательные напряжения пропорциональны углу сдвига :

Соотношение (3.1) представляет собой закон Гука при сдвиге .

Коэффициент пропорциональности G в этой формуле называется модулем сдвига . Видно, что он измеряется в тех же единицах, что и касательное напряжение .

Модуль сдвига G является физической постоянной для материала, характеризующей его жесткость при сдвиге . Значение модуля сдвига G может быть определено экспериментально.

3.5. Какая зависимость существует между модулем сдвига и модулем Юнга ?

Для изотропных материалов эта зависимость имеет вид:

.

Как уже отмечалось ранее, значение коэффициент Пуассона лежит в пределах . Следовательно,

.

Например, для стали любой марки:

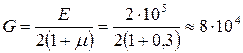МПа.

Аналогичное значение модуля сдвига для стали может быть получено в результате проведения эксперимента на сдвиг (или на кручение).

3.6. Как выглядит диаграмма – при сдвиге?

Вид диаграммы – аналогичен диаграмме – при растяжении, которую мы рассматривали выше. Так, для пластичного материала на ней, в частности, имеются точки, характеризующие предел пропорциональности при сдвиге , предел текучести , а также предел прочности . Последний соответствует срезу образца. Для многих материалов между пределом текучести при сдвиге и пределом текучести при растяжении существует следующая зависимость:

3.7. Чему равна потенциальная энергия деформации при сдвиге?

Если участок стержня длиной испытывает чистый сдвиг, то накапливаемая в нем потенциальная энергия деформации определяется по формуле (подробнее см. беседу 15)

.

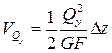3.8. Как записывается условие прочности при сдвиге?

Касательное напряжение, отвечающее безопасной работе материала при сдвиге, называется допускаемым напряжением и обозначается . Для пластичных материалов оно должно быть меньше предела текучести :

а для хрупких материалов – меньше предела прочности :

Тогда условие прочности при сдвиге имеет вид:

. (3.2)

По формуле (3.2) осуществляется проверочный расчет соединений, работающих на срез.

Для определения требуемой площади поперечного сечения (проектировочный расчет ) необходимо воспользоваться следующим неравенством, вытекающим из формулы (3.2):

.

3.9. Что такое срез ? И как правильнее говорить «расчет на сдвиг » или же «расчет на срез »?

Под срезом обычно понимается непосредственное разрушение материала стержня, происходящее в результате деформации сдвига.

Под сдвигом понимается, собственно, угловая деформация или же вид напряженного состояния – чистый сдвиг.

Нам представляется, что, например, при проверке прочности соединений предпочтительнее говорить: «расчет на срез ». Если же мы изучаем напряженное состояние, то правильнее говорить: «напряженное состояние при сдвиге ».

3.10. В некоторых учебниках по сопротивлению материалов для модуля сдвига G встречаются и другие наименования, например, модуль упругости второго рода . Стоит ли использовать этот термин?

Употребление этого термина, как и другого термина «модуль упругости при сдвиге », которые, действительно, иногда можно встретить как в учебной литературе, так и в практике преподавания, мы бы не рекомендовали .

4. Геометрические характеристики
плоских сечений

Ранее мы установили, что прочность и жесткость стержня при растяжении и сжатии определяются площадью его поперечного сечения F :

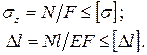
То есть, чем больше площадь поперечного сечения стержня, тем меньше возникающее в нем напряжение и меньше удлинение стержня.

Аналогично в условии прочности при сдвиге мы опять встречаемся с площадью поперечного сечения F :

.

Однако при других видах деформации, в чем мы убедимся в последующих наших беседах, площадь поперечного сечения уже не является той геометрической характеристикой, которая исчерпывающе определяет способность стержня сопротивляться внешней нагрузке.

Возьмем, например, обычную ученическую линейку и начнем ее изгибать . Мы легко убедимся в том, что если расположить линейку «ребром» , то ее изгиб будет значительно меньше, чем в том случае, когда она будет расположена «плашмя» .

Почему? Попробуем ответить на этот вопрос уже сейчас. При изгибе стержня его поперечные сечения поворачиваются вокруг некоторой оси (в дальнейшем мы узнаем, что эта ось называется нейтральной ). И мерой сопротивления этому вращению, как нам известно из теоретической механики, является уже не площадь, а момент инерции поперечного сечения, который существенно зависит от высоты поперечного сечения.

Поэтому в настоящей беседе мы, отвлекаясь от физических свойств материала, и изучим некоторые геометрические характеристики поперечного сечения стержня, которые определяют его способность сопротивляться другим видам деформации, в частности, изгибу и кручению.

4.1. Что называется статическим моментом площади поперечного сечения относительно некоторой оси?

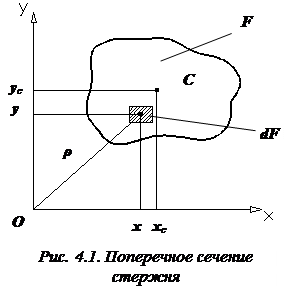Рассмотрим произвольную плоскую фигуру (поперечное сечение стержня) площадью F . Проведем через произвольную точку О оси координат x и y .Выделим элемент площади с координатами x и y (рис. 4.1).

По аналогии с понятием момента силы относительно оси введем понятие статического момента (или просто момента ) площади фигуры относительно оси.

Величину, равную произведению площади на расстояние y до оси x (иными словами, произведение элементарной площади на плечо ), назовем статическим моментом элемента площади относительно оси x :

По аналогии статический момент элемента площади относительно оси y будет равен:

Просуммировав такие произведения по всей площади F , мы получим статические моменты площади всей фигуры относительно осей x и y соответственно:

Статический момент площади фигуры относительно оси измеряется в единицах длины в кубе (как правило, в см 3). Он может быть положительным, отрицательным и, как мы увидим в дальнейшем, равным нулю.

Пусть – координаты центра тяжести фигуры. Продолжая аналогию с моментом силы, можно записать следующие выражения:

Таким образом, статическим моментом площади фигуры относительно оси называется произведение площади фигуры на расстояние от ее центра тяжести до этой оси.

4.2. Как определить координаты центра тяжести поперечного
сечения стержня?

Из формул (4.2) следует, что статический момент площади фигуры относительно центральной оси (то есть оси, проходящей через центр тяжести фигуры) равен нулю .

Сопоставляя (4.1) и (4.2), мы легко получим формулы, позволяющие определить положение центра тяжести поперечного сечения стержня:

Если площадь всей фигуры можно разбить на n простых частей, для которых известны и площадь , и положение центра тяжести и , то вместо формул (4.3) мы получим:

4.3. Что называется осевым , полярным и центробежным моментами инерции фигуры? В каких единицах они измеряются?

Осевым моментом инерции площади фигурыназываетсяинтеграл произведений элементарных площадей на квадраты их расстояний до
рассматриваемой оси. Так, моменты инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y соответственно равны:

Полярным моментом инерции площади фигуры относительно данной точки (полюса) называется интеграл произведений элементарных площадей на квадраты их расстояний до полюса:

Если через полюс проходят две взаимно перпендикулярные оси x и y, то . И тогда

Из формул (4.4) и (4.5) видно, что значения осевых и полярного моментов инерции всегда положительны, поскольку координаты и расстояние входят в них в квадрате.

Центробежным моментом инерции площади фигуры называетсяинтеграл произведений элементарных площадей на их расстояния до осей x и y:

Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см 4).

Понятие о моменте инерции впервые ввел в науку в 1673 г. французский ученый Христиан Гюйгенс (Huygens, 1629 – 1695 гг.).

4.4. Какие оси называются главными осями ?

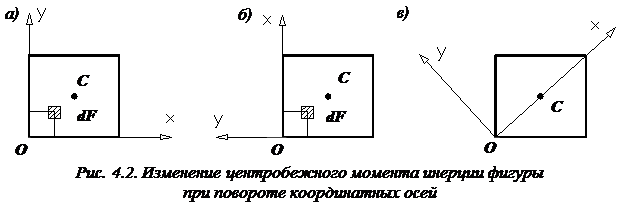
В зависимости от положения координатных осей центробежный момент инерции может быть положительным, отрицательным, а также равным нулю. Рассмотрим, например, квадрат (рис. 4.2, а).

Центробежный момент инерции квадрата относительно осей положителен, так как координаты у всех элементов площади положительные. При повороте осей вокруг начала координат на угол 90 0
(рис. 4.2, б) знак центробежного момента инерции становится отрицательным, так как в этом случае координаты x всех элементарных площадей положительны, а координаты y – отрицательны.

Очевидно, что можно найти такое положение двух взаимно перпендикулярных осей , при котором . Такие оси называются главными осями . Для квадрата такие оси изображены на рис. 4.2, в.

Если фигура имеет ось симметрии , то эта ось является одной из главных осей (другая ось перпендикулярна ей).

Главные оси, проходящие черезцентр тяжести поперечного сечения стержня, называются главными центральными осями .

Понятие о главных осях впервые введено в 1755 г. Яношем Сегнером (Segner, 1704 – 1777 гг.) и, независимо от него, в 1758 г. Леонардом Эйлером (Euler, 1707 – 1783 гг.).

Заметим, что иногда главные оси называют главными осями инерции. Автор рекомендует пользоваться первым определением, поскольку термин инерция к осям не имеет никакого отношения.

4.5. Какие моменты инерции называются собственными
Тогда осевые и центробежный моменты инерции фигуры относительно новых осей и будут определяться по следующим формулам:

Очень часто эти формулы необоснованно приписывают немецкому ученому Якобу Штейнеру (Steiner, 1796 – 1863 гг.). Однако на самом деле они были доказаны еще в 1749 г. Эйлером.

Первые слагаемые в формулах (4.6) ранее нами были названы собственными моментами инерции. Вторые (подчеркнутые) слагаемые в этих формулах называются переносными моментами инерции.

Отметим, что координаты a и b подставляются в формулы (4.6) с учетом их знаков, что является крайне важным, в частности, для третьей из этих формул.