Напряжения от изгибающего момента
Изгиб балки, при котором в сечении возникает только изгибающий момент Мизг, а перерезывающая сила равна нулю, называется чистым изгибом. Чистый изгиб можно осуществить, нагружая брус в концевых сечениях равными по величине и противоположно направленными парами сил, действующими в плоскости симметрии бруса или так, как показано на рис. 6.9.
Равенство нулю перерезывающей силы говорит о том, что при чистом изгибе в поперечных сечениях бруса возникают только нормальные внутренние силы. Изгибающий момент численное значение которого определяется из уравнения (6.2), представляет собой сумму моментов всех элементарных нормальных внутренних сил относительно оси сечения;
![]()
Чтобы с помошью равенства (6.10) определить величину напряжений о в точках сечения, необходимо, как и в случаях растяжения и кручения, определить закон распределения о по плоскости сечения.
Опыт показывает, что при чистом изгибе продольные линии, нанесенные на поверхности бруса, искривляются, а поперечные поворачиваются, но остаются прямыми и перпендикулярными к изогнутым продольным линиям (рис. 6.10). Следовательно, и в данном случае можно применить гипотезу плоских сечений, т. е. считать, что сечения, плоские до деформации, остаются плоскими и после деформации.
Опытным путем также установлено, что волокна на выпуклой стороне бруса испытывают растяжение, а на вогнутой - сжатие.
Поэтому должен существовать слой, волокна которого, искривляясь, сохраняют свою первоначальную длину. Такой слой называется нейтральным, а линия пересечения этого слоя с плоскостью сечения - нейтральной линией сечения.



К заключению о существовании нейтрального слоя приводит и уравнение (6.3). Действительно, при наличии в сечении напряжений разных знаков и непрерывном их распределении по сечению должны существовать точки, где Следовательно, должен существовать слой, волокна которого не испытывают действия ни растягивающих, ни сжимающих сил.
Нейтральная линия делит сечение на две части, в одной из которых действуют растягивающие внутренние силы, а в другой - сжимающие. Вокруг нейтральной линии поворачивается сечение при изгибе. При изгибе в плоскости симметрии бруса нейтральная линия перпендикулярна оси симметрии сечения.
Выделим двумя поперечными сечениями элемент бруса длиной (см. рис. 6.10). При нагружении бруса торцевые сечения этого элемента, оставаясь плоскими, повернутся друг относительно друга вокруг своих нейтральных линий на угол а нейтральный слой искривится, и его радиус кривизны станет равным (рис. 6.11).
Сечение может поворачиваться вокруг нейтральной линии и оставаться при этом плоским только при одинаковых удлинениях продольных волокон, расположенных в слоях, параллельных нейтральному.
Определим относительное удлинение волокна находящегося на расстоянии у от нейтрального слоя. Длина этого волокна до деформации была равна длине нейтрального слоя (нейтральный слой искривляется, но длины не меняет), а после деформации станет равной Тогда
т. е. по высоте сечения удлинения продольных волокон изменяются по линейному закону. Полученный линейный закон распределения деформаций по ширине и высоте сечения является прямым следствием гипотезы плоских сечений.
Введем второе допущение, весьма упрощающее решение задачи о напряжениях при изгибе. Предположим, что продольные волокна при изгибе друг на друга не давят и находятся таким образом в
состоянии одноосного растяжения или сжатия Согласно этому допущению связь между удлинениями волокон и напряжениями а в поперечных сечениях бруса описывается законом Гука для одноосного нагружения: Без такого допущения надо было бы применить закон Гука для трехосного нагружения (см. выражения 2.33).
Подставляя формулу (6.11) в равенство получаем
Итак, напряжения а, как и деформации по ширине сечения постоянны, а по высоте сечения изменяются пропорционально расстоянию точки от нейтральной линии. Эпюра а приведена на рис. 6.11.
Положение нейтральной линии определим из условия равенства нулю нормальной силы в сечениях бруса при поперечном изгибе:
Этот последний интеграл представляет собой статический момент всего сечения относительно нейтральной линии. Он может быть равен нулю только относительно центральной оси. Следовательно, нейтральная линия проходит через центр тяжести сечения и поэтому является его нейтральной осью. Кроме того, она перпендикулярна оси симметрии сечения и является поэтому главной осью инерции сечения. Таким образом, при прямом поперечном изгибе нейтральная линия совпадает с главной центральной осью инерции сечения, перпендикулярной плоскости действия нагрузки.
Подставляя закон распределения напряжений (6.12) в уравнение (6.10), получаем
![]()
Отсюда находим формулу для определения кривизны нейтрального слоя балки
Последнее уравнение аналогично выражениям и является, в сущности, уравнением деформаций при изгибе.
Исключая из уравнений (6.12) и (6.13) радиус кривизны, находим расчетное уравнение для нормальных напряжений при изгибе


Здесь - момент инерции сечения относительно его нейтральной оси, а у - расстояние от этой оси до точки, в которой определяется напряжение.
Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной оси,
![]()
Частное от деления главного момента инерции сечения на расстояние от нейтральной оси до наиболее удаленной от нее точки сечения называется моментом сопротивления изгибу и обозначается или
![]()
Таким образом,
![]()
Понятие момента сопротивления вводится обычно лишь для сечений, симметричных относительно нейтральной оси. Момент сопротивления изгибу прямоугольника а кольца с внутренним диаметром и внешним
Для сечения, представленного на рис. 6.12, момент сопротивления вычисляется так:
![]()
Следует иметь в виду, что сложной фигуры не равен сумме моментов сопротивления изгибу ее частей.
В предыдущих выводах предполагалось, что брус имеет продольную плоскость симметрии и в этой плоскости действует внешняя нагрузка. Распространим теперь полученные результаты на случай несимметричных сечений (рис. 6.13). Для этого обратимся к уравнениям равновесия отсеченной части бруса (см. разд. 6.2). При чистом изгибе бруса в одной из координатных плоскостей, например нормальные напряжения о, определяемые формулой (6.14),
Рассмотрим балку, испытывающую чистый изгиб парами (Рис.5.3).

Разрежем балку
сечением
 не две части и рассмотрим условия
равновесия одной из них, например, левой,
показанной на рис.5.3 внизу. Для простоты
чертежа балка взята прямоугольного
сечения. Так как практически искривления
балки ничтожны по сравнению с ее
размерами, то отсеченная часть изображена
недеформированной.
не две части и рассмотрим условия
равновесия одной из них, например, левой,
показанной на рис.5.3 внизу. Для простоты
чертежа балка взята прямоугольного
сечения. Так как практически искривления
балки ничтожны по сравнению с ее
размерами, то отсеченная часть изображена
недеформированной.
Линия пересечения
плоскости симметрии балки с плоскостью
сечения принята за ось
 .
Нейтральная линия сечения принята за
ось
.
Нейтральная линия сечения принята за
ось ,
причем положение ее по высоте балки
пока неизвестно. Ось
,
причем положение ее по высоте балки
пока неизвестно. Ось взята вдоль нейтрального слоя
перпендикулярно осям
взята вдоль нейтрального слоя
перпендикулярно осям и
и .
.
В каждой точке
поперечного сечения действуют нормальные
напряжения
 .
Выделив вокруг любой точки с координатами
.
Выделив вокруг любой точки с координатами и
и элементарную площадку
элементарную площадку ,
обозначим действующую на ней силу
,
обозначим действующую на ней силу .
.
Отсеченная часть
балки находится в равновесии под
действием внешних сил, образующих пару
 ,
и нормальных усилий
,
и нормальных усилий ,
заменяющих отброшенную часть балки.
Для равновесия эта система должна
удовлетворять шести уравнениям статики.
Составим сначала уравнения равновесия
проекций сил на три координатные оси
,
заменяющих отброшенную часть балки.
Для равновесия эта система должна
удовлетворять шести уравнениям статики.
Составим сначала уравнения равновесия
проекций сил на три координатные оси ,
, и
и .
.
Так как проекция
пары
 на любую ось равна нулю, то эти уравнения
дают равенство суммы проекций нормальных
усилий
на любую ось равна нулю, то эти уравнения
дают равенство суммы проекций нормальных
усилий на оси. Заменяя суммирование этих усилий
по всей площади сечения интегрированием,
получим:
на оси. Заменяя суммирование этих усилий
по всей площади сечения интегрированием,
получим:
 .
(5.3)
.
(5.3)
 и
и
![]() обращаются в тождества 0
обращаются в тождества 0 0, так как усилия
0, так как усилия
 проектируются
на эти оси в точку.
проектируются
на эти оси в точку.
Составим теперь
уравнения моментов относительно осей
 ,
, и
и .
Заметим при этом, что пара
.
Заметим при этом, что пара лежит в плоскости
лежит в плоскости и поэтому моментов относительно осей
и поэтому моментов относительно осей и
и не дает.
не дает.
 обращается в
тождества, так как усилия
обращается в
тождества, так как усилия
 параллельны оси
параллельны оси .
.
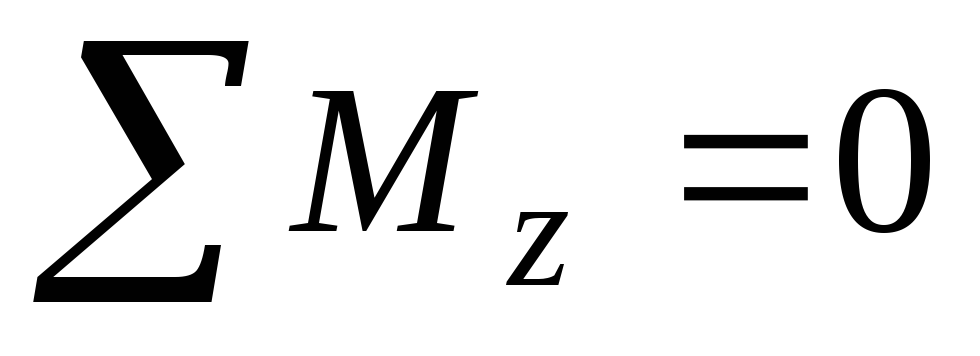 ;
;
 ,
,
 ,
(5.4)
,
(5.4)
 ;
;
 .
(5.5)
.
(5.5)
Таким образом, из шести уравнений равновесия можно использовать только три:
 или
или
 ,
(5.6)
,
(5.6)
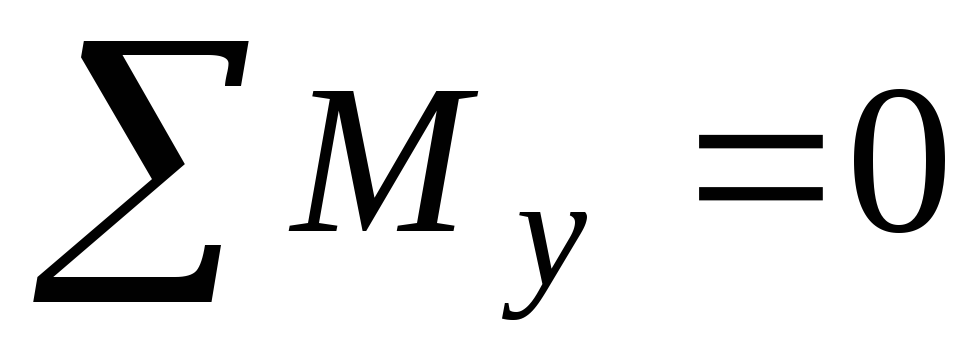 ;
или
;
или
 ,
(5.7)
,
(5.7)
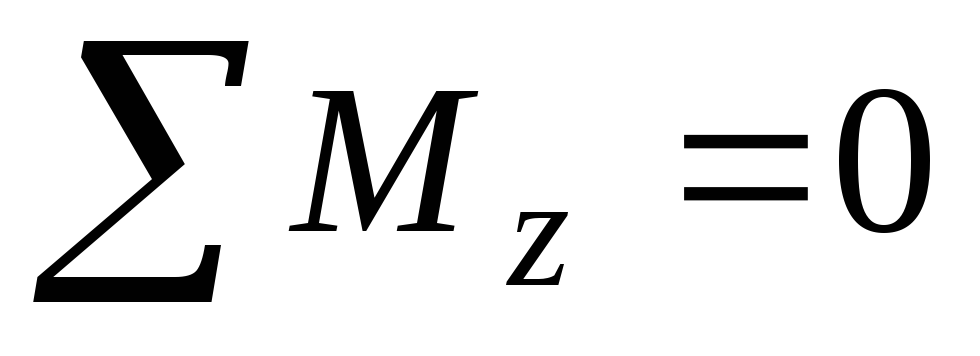 ;
или
;
или
 .
(5.8)
.
(5.8)
Полученных трех
уравнений статики недостаточно для
определения величины нормальных
напряжений, так как
 изменяется в зависимости от расстояния
изменяется в зависимости от расстояния площадки
площадки до нейтральной линии по неизвестному
пока закону. Это расстояние
до нейтральной линии по неизвестному
пока закону. Это расстояние тоже пока неизвестно, так как неизвестно
положение нейтральной линии
тоже пока неизвестно, так как неизвестно
положение нейтральной линии .
.
Задача оказывается
статически неопределимой, поэтому
рассмотрим деформации балки. Для этого
двумя бесконечно близкими сечениями
 и
и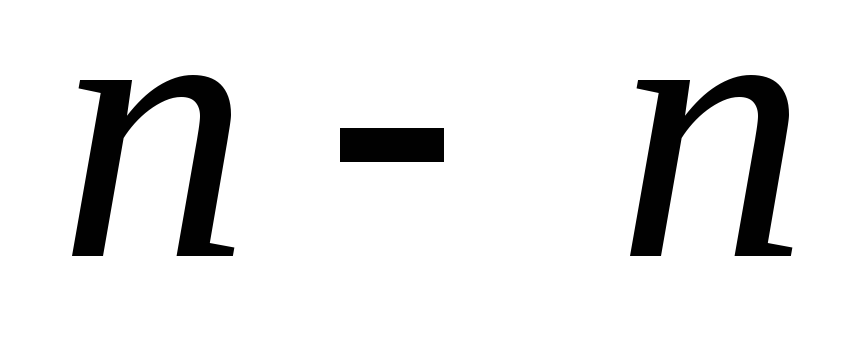 выделим из балки элемент длиной
выделим из балки элемент длиной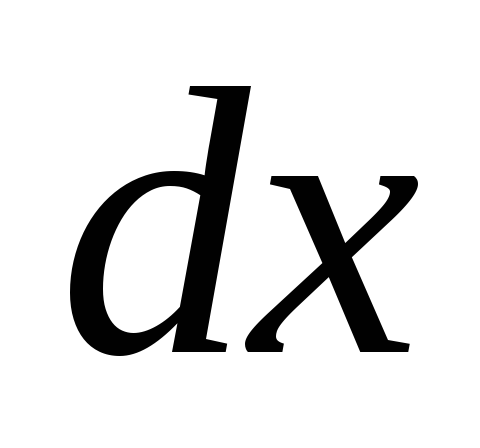 .
Вид этого элемента до и после деформации
приведен на рис 5.4.
.
Вид этого элемента до и после деформации
приведен на рис 5.4.

Оба поперечных
сечения, оставаясь плоскими, повернулись
вокруг нейтральной линий (на рисунке
точки
 и
и )
и образуют угол
)
и образуют угол .
Нейтральный слой показан пунктиром.
Линия
.
Нейтральный слой показан пунктиром.
Линия ,
принадлежащее нейтральному слою, после
деформации сохраняет свою первоначальную
длину
,
принадлежащее нейтральному слою, после
деформации сохраняет свою первоначальную
длину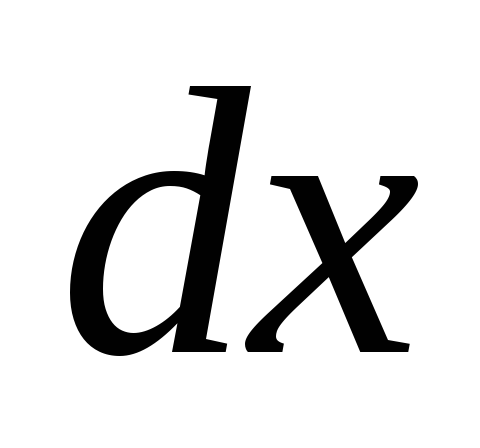 .
Все волокна, лежащие выше нейтрального
слоя, укорачиваются, а ниже
удлиняются.
.
Все волокна, лежащие выше нейтрального
слоя, укорачиваются, а ниже
удлиняются.
Найдем удлинение
какого-либо волокна АB,
расположенного на расстоянии
 от нейтрального слоя и растянутого
напряжениями
от нейтрального слоя и растянутого
напряжениями .
Первоначальная длина этого волокна
.
Первоначальная длина этого волокна .
После деформации его длина стала
.
После деформации его длина стала .
Абсолютное удлинение рассматриваемого
волокна.
Относительное удлинение равно
.
Абсолютное удлинение рассматриваемого
волокна.
Относительное удлинение равно
 ,
,
т.е. удлинения волокон пропорциональны их расстояниям до нейтрального слоя.
Здесь

радиус кривизны нейтрального слоя,
величину которого для выделенного
(бесконечно малого по длине) элемента
можно считать постоянной. Допустив, что
при изгибе волокна друг на друга не
давят, и что каждое волокно испытывает
простое растяжение или сжатие, для
вычисления напряжений можем воспользоваться
законом Гука при растяжении:
радиус кривизны нейтрального слоя,
величину которого для выделенного
(бесконечно малого по длине) элемента
можно считать постоянной. Допустив, что
при изгибе волокна друг на друга не
давят, и что каждое волокно испытывает
простое растяжение или сжатие, для
вычисления напряжений можем воспользоваться
законом Гука при растяжении:
 или
или
 .
(5.9)
.
(5.9)
Уравнение (5.9)
показывает, что величина нормальных
напряжений при изгибе меняется прямо
пропорционально расстоянию
 рассматриваемой точки сечения от
нейтрального слоя. Значит, напряжения
распределены по высоте сечения по
линейному закону. В нейтральном слое
при
рассматриваемой точки сечения от
нейтрального слоя. Значит, напряжения
распределены по высоте сечения по
линейному закону. В нейтральном слое
при напряжения
напряжения ,
в сжатой зоне (при
,
в сжатой зоне (при )
напряжения становятся отрицательными,
в растянутой зоне (при
)
напряжения становятся отрицательными,
в растянутой зоне (при )
напряжения становятся положительными.
По мере удаления от нейтрального слоя
напряжения растут по абсолютной величине
и достигают максимальных значений при
)
напряжения становятся положительными.
По мере удаления от нейтрального слоя
напряжения растут по абсолютной величине
и достигают максимальных значений при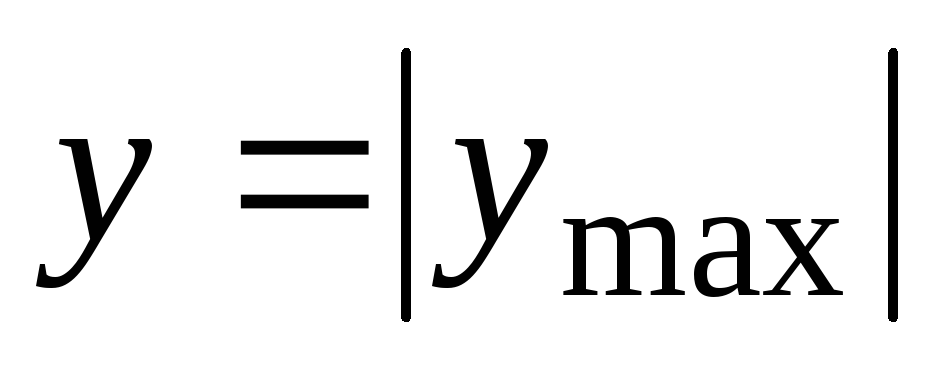 ,
т.е. в самых удаленных от нейтрального
слоя волокнах.
,
т.е. в самых удаленных от нейтрального
слоя волокнах.
Формула (5.9) дает
характер распределения нормальных
напряжений по высоте сечения (Рис.5.5),
но ею нельзя воспользоваться для
вычисления величины напряжений, так
как ни
 ,
ни
,
ни неизвестны, поскольку неизвестно
расположение нейтрального слоя по
высоте сечения.
неизвестны, поскольку неизвестно
расположение нейтрального слоя по
высоте сечения.

Для определения величины нормальных напряжений в зависимости от величины изгибающего момента обратимся к совместному решению полученного из рассмотрения деформаций уравнения (5.9) и уравнений статики (5.6)(5.8).
Подставляя значение
 из выражения (5.9) в уравнение (5.6), получим:
из выражения (5.9) в уравнение (5.6), получим:
 или
или
 .
.
Так как
 ,
то
,
то
 .
.
Этот интеграл
представляет собой статический момент
площади относительно нейтральной линии
сечения. Так как он равен нулю, то,
следовательно, нейтральная линия сечения
проходит через центр тяжести сечения.
Так как центр тяжести лежит и на оси
симметрии
 ,
то точка пересечения этих двух осей
,
то точка пересечения этих двух осей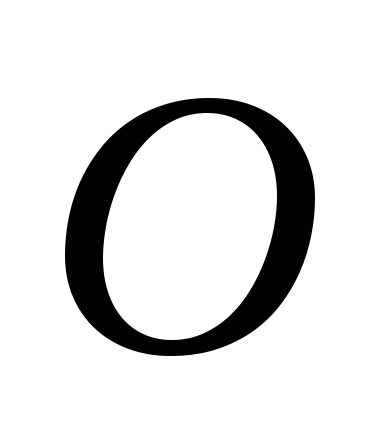 является центром тяжести сечения, а ось
является центром тяжести сечения, а ось
осью балки.
осью балки.
Таким образом, положение нейтральной оси и нейтрального слоя вполне определены. Нейтральный слой заключает в себе центры тяжести всех сечений балки.
Подставим выражение (5.9) в уравнение (5.7). Получим:
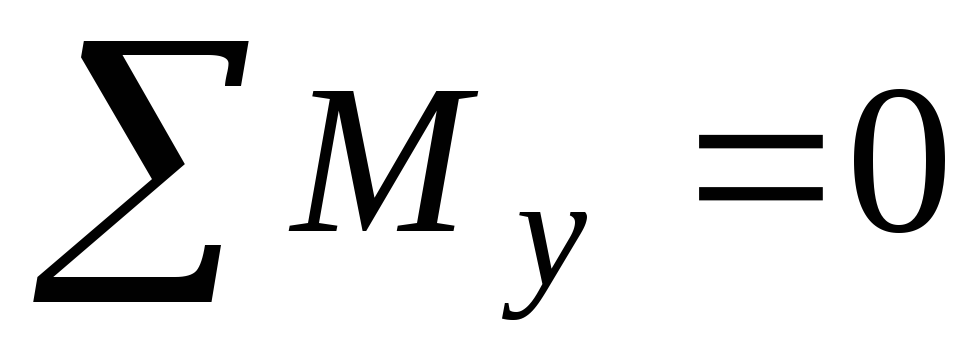 ,
,
 или
или .
.
Отсюда следует, что
 .
.
Полученный интеграл представляет собой центробежный момент инерции. Известно, что оси, относительно которых центробежный момент инерции равен нулю, являются главными осями инерции. Следовательно, нейтральная линия сечения является главной осью инерции сечения. А это означает, что осевой момент инерции относительно этой линии достигает экстремальной величины.
Воспользуемся последним уравнением равновесия (5.8), подставив в него выражение (5.9). Получим:
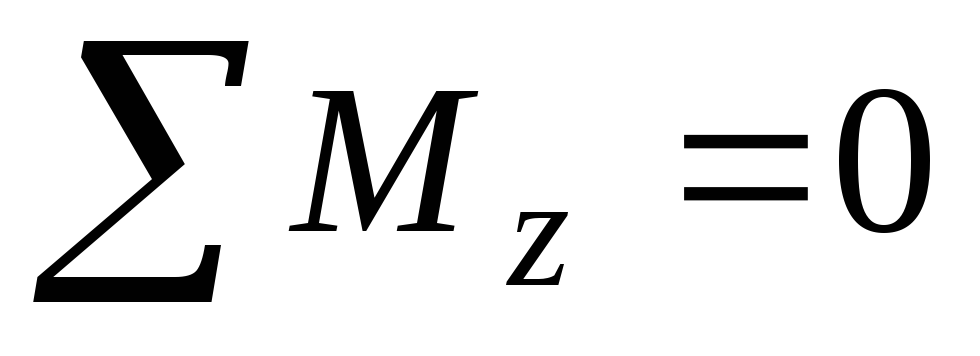 ;
;
 или
или .
(5.10)
.
(5.10)
Выражение
 представляет собой момент инерции
сечения относительно нейтральной линии
сечения
представляет собой момент инерции
сечения относительно нейтральной линии
сечения и обозначается буквой
и обозначается буквой .
.
Таким образом, (5.10) можно переписать в виде:
 .
(5.11)
.
(5.11)
Преобразуем это выражение к виду:
 .
(5.12)
.
(5.12)
Из формулы (5.12)
видно, что чем больше при данном изгибающем
моменте момент инерции
 ,
тем большим окажется радиус кривизны
нейтрального слоя, а, следовательно, и
оси балки, т.е. тем меньше балка изогнется.
,
тем большим окажется радиус кривизны
нейтрального слоя, а, следовательно, и
оси балки, т.е. тем меньше балка изогнется.
Величина момента
инерции является геометрическим фактором
жесткости балки при изгибе, так как
характеризует способность балки
искривляться в зависимости от размеров
и формы поперечного сечения балки.
Произведение
 называется
жесткостью балки при изгибе, и чем она
больше, тем меньше изогнется балка при
действии данного изгибающего момента.
называется
жесткостью балки при изгибе, и чем она
больше, тем меньше изогнется балка при
действии данного изгибающего момента.
Подставим в
выражение (5.12) значение
![]() .
Получим:
.
Получим:
 .
(5.13)
.
(5.13)
Таким образом, нормальные напряжения в любой точке сечения прямо пропорциональны величине изгибающего момента и расстоянию точки от нейтральной линии сечения и обратно пропорционально моменту инерции сечения относительно нейтральной оси. Знак “”в формуле (5.13) позволяет автоматически получать правильный знак для напряжения в зависимости от координаты точки, в которой это напряжение вычисляется.
Рассмотрим пример определения нормального напряжения в произвольной точке сечения изгибаемой балки.
Пример
5.1.
Определить нормальное напряжение
при изгибе балки (в МПа) в точке А
поперечного сечения, удаленной от
нейтральной линии сечения на 15 см
(Рис.5.6), если изгибающий
момент кНм.
кНм.

 см 4 .
см 4 .
2. Подставляем значения изгибающего момента, осевого момента инерции и координаты точки А в формулу для нормальных напряжений (5.13) и находим напряжения:
 кНм.
кНм.
Таким образом, в
точке А поперечного сечения балки
действует сжимающее нормальное напряжение
 МПа.
МПа.
Чистый изгиб – это самый простой случай нагружения балки (рис.5.10). Он имеет место и при другой схеме нагружения (рис.5.13.). Силовая плоскость совпадает с одной из главных осей поперечного сечения – осью y (рис.5.13). В сечении действует только нормальное напряжение σ, касательное τ равно нулю ввиду равенства нулю поперечной силы Q.
Формулу для σ можно вывести только из рассмотрения картины деформации балки (рис.5.14,б). Опыты, поставленные на эластичных (например, резиновых) моделях, позволяющих легко получить значительные деформации, показывают, что нанесённая на поверхность прямоугольная сетка линий (рис.5.14,а) деформируется (рис.5.14,б) следующим образом:
а) продольные линии искривляются по дуге окружности;
б) контуры поперечных сечений остаются прямыми;
в) линии контуров сечений пересекаются с продольными волокнами под прямым углом.
Далее,
замеряя расстояния между аналогичными
точками контура каких-либо двух сечений,
можно обнаружить, что при деформации
верхние продольные волокна укорачиваются
(),
а нижние – удлиняются ( ).
Ясно, что есть такие волокна, длина
которых остается неизменной (
).
Ясно, что есть такие волокна, длина
которых остается неизменной ( ),
они лишь искривляются. Совокупность
волокон, не меняющих своей длины при
изгибе балки, называется
нейтральным слоем (НС).
Поперечное сечение пересекается с
нейтральным слоем по прямой, которая
называется нейтральной
линией (НЛ).
),
они лишь искривляются. Совокупность
волокон, не меняющих своей длины при
изгибе балки, называется
нейтральным слоем (НС).
Поперечное сечение пересекается с
нейтральным слоем по прямой, которая
называется нейтральной
линией (НЛ).
Таким образом, при чистом изгибе балка деформируется следующим образом.
1. Плоские поперечные сечения остаются плоскими и поворачиваются так, что остаются нормальными к изогнутой оси – справедлива гипотеза плоских сечений.
2. Продольные волокна удлиняются и укорачиваются, но друг на друга не давят – имеет место линейное напряжённое состояние.
3. В поперечном направлении (вдоль оси z) деформация постоянна.
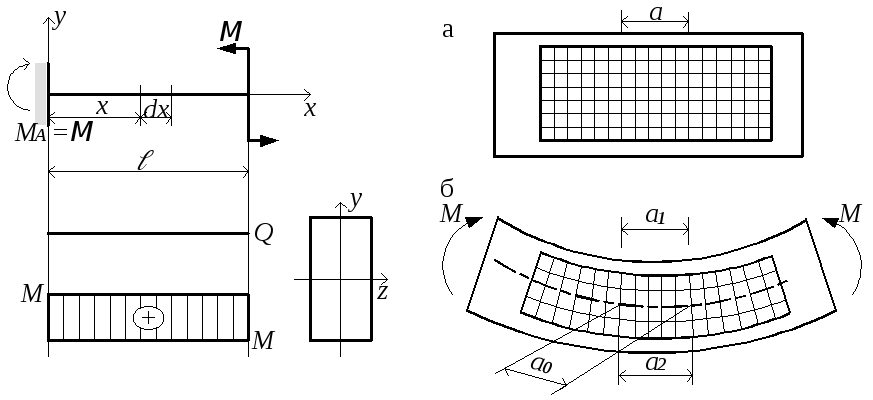
Рис.5.13 Рис.5.14
Выделим
элемент двумя смежными поперечными
сечениями m-m
и n-n,
отстоящими друг от друга на расстоянии
dx
(рис.5.15,а), и, приняв во внимание гипотезу
плоских сечений, покажем его деформированное
состояние (рис.5.15,б). Сечения m-m
и n-n
остаются плоскими и поворачиваются на
угол dθ,
элемент a 0 b 0
нейтрального слоя превращается в дугу
 с радиусом ρ.
Волокна нейтрального слоя не изменяют
своей длины при деформации, поэтому
с радиусом ρ.
Волокна нейтрального слоя не изменяют
своей длины при деформации, поэтому
 ,
,
 . (5.8)
. (5.8)
Произвольное
волокно
 ,
находящееся на расстоянии y
от нейтрального слоя, превращается в
криволинейное волокно
,
находящееся на расстоянии y
от нейтрального слоя, превращается в
криволинейное волокно
 .
Абсолютное удлинение его ∆ab
может быть показано на рис.5.15,б, если из
точки b′ 0
провести прямую, параллельную Cm
.
Абсолютное удлинение его ∆ab
может быть показано на рис.5.15,б, если из
точки b′ 0
провести прямую, параллельную Cm
 , (5.9)
, (5.9)
Относительное удлинение этого волокна
 . (5.10)
. (5.10)
Подставив выражение (5.8) в выражение (5.10), получим
 . (5.11)
. (5.11)
Таким образом, рассмотрение геометрической стороны задачи показало, что относительная продольная деформация пропорциональна расстоянию волокна от нейтральной оси.
 . (5.13)
. (5.13)
Формулой (5.13) пока пользоваться невозможно, т.к. неизвестны радиус кривизны нейтрального слоя ρ и положение нейтральной оси в сечении. Для определения этих величин рассмотрим статическую сторону задачи (рис.5.16).
Запишем уравнения статики для отрезка балки длиной x, находящегося под действием постоянного изгибающего момента M и нормальных напряжений σ.
Нужно записать шесть уравнений статики
∑х = 0, ∑у = 0, ∑z = 0,
∑M x = 0, ∑M y = 0, ∑M z = 0.
Из них три дают тождество 0 = 0. Остаются три уравнения
∑х = 0, ∑M y = 0, ∑M z = 0.
Запишем их по порядку, подставляя σ по формуле (5.13).
![]() . (5.14)
. (5.14)
Поскольку
 ,
,
 ,
а это статический момент сечения
относительно нейтральной линии.
,
а это статический момент сечения
относительно нейтральной линии.
 . (5.15)
. (5.15)

По
той же причине, что и в предыдущем
уравнении,
 .
Это другая геометрическая характеристика
сечения – центробежный момент инерции
.
Это другая геометрическая характеристика
сечения – центробежный момент инерции
 . (5.16)
. (5.16)
На основании равенства (5.15) заключаем, что ось z – нейтральная линия сечения – проходит через центр тяжести поперечного сечения. Равенство (5.16) показывает, что оси y и z – главные центральные оси сечения. Этим определяется положение нейтральной линии сечения.
Таким образом, если силовая линия совпадает с одной из главных центральных осей сечения, то изгиб будет плоским и нейтральная линия сечения совпадает с другой главной центральной осью.
Из третьего уравнения (5.13) определим радиус кривизны нейтрального слоя.
Вспомнив,
что
 ,
представляет собой момент инерции
сечения относительно оси z,
можем последнюю формулу записать в
виде
,
представляет собой момент инерции
сечения относительно оси z,
можем последнюю формулу записать в
виде
 . (5.17)
. (5.17)
Наконец, подставив формулу (5.17) в выражение (5.13), получим формулу для нормального напряжения при чистом изгибе
 . (5.18)
. (5.18)
Формула (5.17) в приведённом выводе была вспомогательной, однако она имеет и большое самостоятельное значение. Её можно трактовать как закон Гука при изгибе, поскольку она связывает деформацию (кривизну нейтрального слоя 1/ρ) с действующим изгибающим моментом.
Произведение EJ носит название жёсткости сечения при изгибе и имеет размерность кНсм 2 .

Формула (5.18) показывает, что величина σ линейно возрастает по мере удаления от нейтральной линии (рис.5.17). При этом напряжения постоянны по ширине сечения. При изменении знака изгибающего момента поменяется и знак напряжений (верхние волокна окажутся растянутыми, нижние – сжатыми).


