Касательные напряжения в сплошном круглом сечении. Кручение бруса прямоугольного сечения

стержня круглого сечения

Крутящие моменты представляют собой равнодействующие внутренних сил. При кручении стержня в его поперечных сечениях возникают непрерывно распределённые касательные напряжения, которые нужно уметь определять при расчётах на прочность.

Нанесём на круглый стержень ортогональную сетку и нагрузим его внешним моментом Т (рис. 6.9). По результатам этого опыта можно сделать следующие выводы:

1) прямоугольники ортогональной сетки превратились в параллелограммы, следовательно, в поперечных сечениях действуют касательные напряжения;

2) расстояния между линиями, нормальными оси стержня, и длина всего стержня не изменились. Не изменился также и диаметр стержня. Можно предположить, что каждое поперечное сечение поворачивается в своей плоскости на некоторый угол, оставаясь плоским и нормальным к оси (гипотеза Бернулли). На основании этой гипотезы делаем вывод о том, что радиусы всех поперечных сечений повернулись на определённые углы, оставаясь прямолинейными. Таким образом, точка К переместится в положение К´ по дуге радиуса r , а точка N – в

по дуге меньшего радиуса(рис. 6.10).

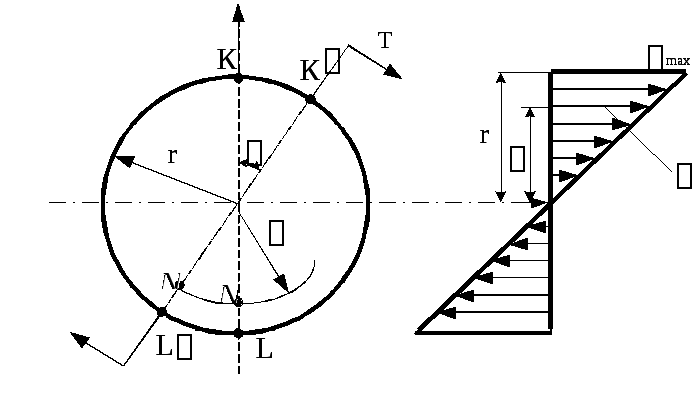
На основании этого можно сделать вывод, что при кручении круглого стержня в его поперечных сечениях действуют только касательные напряжения, а нормальные напряжения отсутствуют, т.е. мы имеем случай чистого сдвига.

Для того чтобы установить закон распределения касательных напряжений по поперечному сечению круглого стержня, нагруженного крутящим моментом Т, рассмотрим его деформацию между сечениями I и II (рис. 6.9 и рис. 6.11).

Угол сдвига элемента ABCD, расположенного на поверхности стержня:

Угол сдвига элемента, расположенного на расстоянии от оси стержня:

(6.10)

На основании закона Гука для сдвига можно записать

(6.11)

Из (6.11) следует, что при кручении касательные напряжения и деформациипрямо пропорциональны расстоянию от центра тяжести сечения. В центре тяжести круглого сечения касательные напряжения равны нулю, наибольшее значение они принимают на поверхности стержня. Эпюра касательных напряжений в поперечном сечении круглого стержня изображена на рис. 6.10.

Определим касательные напряжения из условия, что крутящий момент в сечении представляет собой равнодействующий момент от касательных напряжений (рис. 6.12).

, (6.12)

где

– элементарная сила, действующая на площадке

.

Подставим в (6.12) касательные напряжения из (6.11):

. (6.13)

Интеграл

представляет собой полярный момент инерции круглого сеченияJ p , следовательно,

, откуда

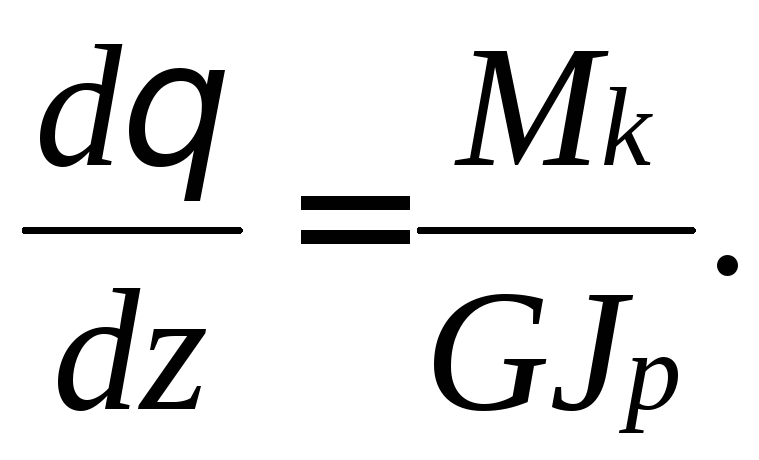(6.14)

Подставим значение

в формулу (6.11) и получим

(6.15)

Из (6.15) следует, что в точках, равноудалённых от центра сечения, касательные напряжения одинаковы. Наибольшие напряжения возникают в точках, расположенных на поверхности стержня, где

.

(6.16)

где величина

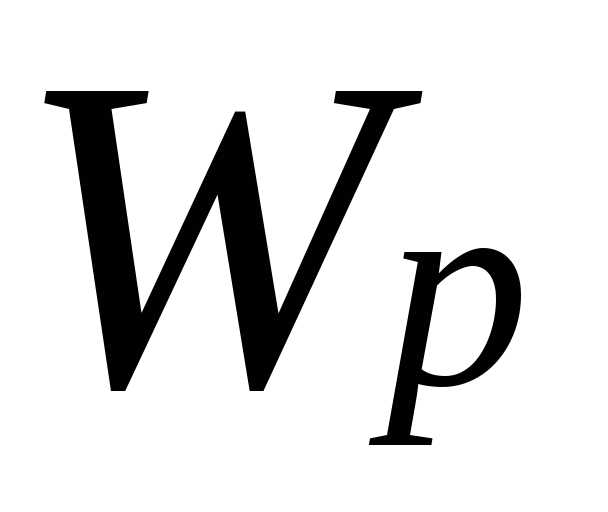, представляющая геометрическую характеристику плоского сечения, носит название полярного момента сопротивления или момента сопротивления при кручении:

(6.17)

Для круглого сплошного сечения

. (6.18)

Для кольцевого сечения (рис. 5.5)

где

.

Запишем условие статической прочности при кручении, обозначив допускаемое касательное напряжение через

(6.20)

Величину принимают равной 0,5 – 0,6 допускаемого напряжения на растяжение. Уравнение (6.20) можно использовать только для круглых валов, как сплошных, так и полых; для валов других сечений его применять нельзя. Используя условие прочности, можно рассчитать диаметр вала либо определить максимальный допускаемый крутящий момент, который может передать вал. Подставим в формулу (6.20) выражение полярного момента сопротивления

(6.21)

(6.22)

Аналогично для полых валов можно записать

(6.23)

Допускаемый из условия статической прочности при кручении

максимальный крутящий момент определяют по формуле

(6.24)

Под действием внешнего скручивающего момента, приложенного на правом конце вала (рис. 7.2), левый конец которого жестко закреплен, стержень будет закручиваться. При этом любое сечение стержня, оставаясь плоским, будет поворачиваться на некоторый угол φ к, называемый углом закручивания. Этот угол изменяется по длине вала от нуля в заделке до максимального на правом конце вала. При этом образующая внешней цилиндрической поверхности вала повернется на угол γ , называемый углом сдвига. Этот угол изменяется вдоль радиуса сечения от нуля на оси вала до - γ max на внешней поверхности. Опыт показывает, что после закручивания бруса круглого сечения поперечные линии, нанесенные на его поверхности, остаются плоскими, а диаметры сечений и расстояния между ними не изменяются. При этом прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных сечениях бруса, а по закону парности касательных напряжений – и в продольных его сечениях, то есть напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг . На основании опыта вводятся следующие гипотезы :

1. Нормальные напряжения в поперечных сечениях отсутствуют (иначе изменялись бы расстояния между сечениями).
2. Поперечные сечения при кручении остаются плоскими.
3. Радиусы в поперечных сечениях остаются прямолинейными (не искривляются).

С учетом указанных гипотез геометрическая картина деформаций вала представлена на рис. 7.2. Рассмотрим, вырезанный из вала клиновидный элемент (см. рис. 7.2) длиной dx . Из рисунка видно, что

что касательные напряжения в сечении вала изменяются по радиусу по линейному закону.

При чистом кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей – крутящему моменту относительно нормальной к сечению оси. Касательные напряжения перпендикулярны радиусам , проведенным через точки их действия (рис. 7.3).

Для доказательства этого будем исходить от противного, то есть, предположим, что касательное напряжение не перпендикулярно радиусу. Это означает, что в каждой точке сечения, кроме касательных напряжений, перпендикулярных радиусам, действуют радиально направленные касательные напряжения. Но если это так, то по закону парности и на цилиндрической поверхности радиуса ρ или r будет действовать касательное напряжение, что неверно, так как на боковой поверхности нет напряжений.

Крутящий момент в сечении бруса определяется из уравнения (3.5):

или в более краткой записи

где - есть полярный момент инерции сечения. С учетом уравнения (7.3) можно определить касательное напряжение в произвольной точке поперечного сечения вала, определяемой радиусом ρ :

где W p - полярный момент сопротивления.

Эпюра распределения касательных напряжений по радиусу показана на рисунке 7.4 для сплошного и полого валов.

Угол закручивания вала нетрудно определить на основе полученного выше уравнения.

При этом нарушается закон плоских сечений, сечения некруглой формы при кручении искривляются – депланация поперечного сечения.

Эпюры касательных напряжений прямоугольного сечения.

; , J k и W k - условно называют моментом инерции и моментом сопротивления при кручении. W k = ahb 2 ,

J k = bhb 3 , Максимальные касательные напряжения t max будут посредине длинной стороны, напряжения по середине короткой стороны: t= g×t max , коэффициенты: a,b,g приводятся в справочниках в зависимости от отношения h/b (например, при h/b=2, a=0,246; b=0,229; g=0,795.

Изгиб

Плоский (прямой) изгиб - когда изгибающий момент действует в плоскости, проходящей через одну из главных центральных осей инерции сечения, т.е. все силы лежат в плоскости симметрии балки. Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы : продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются. .

Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: , r - радиус кривизны нейтрального слоя, y - расстояние от некоторого волокна до нейтрального слоя. Закон Гука при изгибе : , откуда (формула Навье): , J x - момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента, EJ x - жесткость при изгибе, - кривизна нейтрального слоя.

Максимальные напряжения при изгибе возникают в точках, наиболее удаленных от нейтрального слоя: , J x /y max =W x -момент сопротивления сечения при изгибе, . Если сечение не имеет горизонтальной оси симметрии, то эпюра нормальных напряжений s не будет симметричной. Нейтральная ось сечения проходит через центр тяжести сечения. Формулы для определения нормального напряжения для чистого изгиба приближенно годятся и когда Q¹0. Это случай поперечного изгиба . При поперечном изгибе, кроме изгибающего момента М, действует поперечная сила Q и в сечении возникают не только нормальные s, но и касательные t напряжения. Касательные напряжения определяются формулой Журавского: , где S x (y) - статический момент относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии "y" от нейтральной оси; J x - момент инерции всего поперечного сечения относительно нейтральной оси, b(y) - ширина сечения в слое, на котором определяются касательные напряжения.

Для прямоугольного сечения: , F=b×h, для круглого сечения: , F=p×R 2 , для сечения любой формы ,

k- коэфф., зависящий от формы сечения (прямоугольник: k= 1,5; круг - k= 1,33).

M max и Q max определяются из эпюр изгибающих моментов и поперечных сил. Для этого балка разрезается на две части и рассматривается одна из них. Действие отброшенной части заменяется внутренними силовыми факторами М и Q, которые определяются из уравнений равновесия. В некоторых вузах момент М>0 откладывается вниз, т.е. эпюра моментов строится на растянутых волокнах. При Q= 0 имеем экстремум эпюры моментов. Дифференциальные зависимости между М,Q и q :

q - интенсивность распределенной нагрузки [кН/м]

Главные напряжения при поперечном изгибе :

.

Расчет на прочность при изгибе : два условия прочности, относящиеся к различным точкам балки: а) по нормальным напряжениям , (точки наиболее удаленные от С); б) по касательным напряжениям , (точки на нейтр.оси). Из а) определяют размеры балки: , которые проверяют по б). В сечениях балок могут быть точки, где одновременно большие нормальные и большие касательные напряжения. Для этих точек находятся эквивалентные напряжения, которые не должны превышать допустимых. Условия прочности проверяются по различным теориям прочности