Плоский чистый изгиб. Поперечный и чистый изгиб

⁰

Под изгибом понимают такой вид деформации бруса, при котором его ось изменяет свое положение в пространстве. При этом его поперечные сечения совершают поступательное и угловое перемещения.

Брус, работающий на изгиб, называют балкой . Если внешние нагрузки расположены в плоскости, совпадающей с одной из главных центральных плоскостей, то имеет место плоский прямой изгиб .

Плоский изгиб может быть поперечным и чистым. При поперечном изгибе в сечении бруса возникают поперечные силы и изгибающие моменты (рисунок 12.1,а ). В этом случае сечения сдвигаются параллельно одно другому и поворачиваются на некоторый угол. При чистом изгибе возникают только изгибающие моменты, а сечения поворачиваются относительно друг друга на угол (рисунок 12.1,б).

Рисунок 12.1

Рассмотрим брус, подвергающийся деформации изгиба (рисунок 12.2).

Его сечения поворачиваются на некоторый угол, но остаются плоскими. Происходит растяжение одних и сжатие других волокон. Вследствие удлинения одних и укорочения других волокон под действием момента М в поперечных сечениях бруса возникают нормальные напряжения . Поперечные силы Q вызывают сдвиг, и в брусе возникают касательные напряжения. Рисунок 12.2

Конец работы -

Эта тема принадлежит разделу:

ПРИКЛАДНАЯ МЕХАНИКА

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА... Кафедра Техническая физика и теоретическая механика...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Деформация изгиба рассматривается на примере тела, имеющего простую форму. Например, брус. Брусом называется твёрдое тело, у которого длина значительно больше поперечных величин одного порядка. Ось бруса может быть кривой или прямой линией. Брусья с прямолинейной осью называются стержнями, балками, стойками, в зависимости от назначения.

Брусья с прямолинейной осью, положенные на опоры и изгибаемые приложенными к ним нагрузками (равномерно распределённая нагрузка, сосредоточенная сила, изгибающий момент) называются балками.

Балки служат для передачи действующих на них нагрузок на опоры, на которых они покоятся. Если балка имеет свешивающиеся концы, такую балку принято называть консольной, свешивающиеся концы – консолями. На опорах балки возникают реакции, с определения которых следует начинать решение всех задач, связанных с изгибом балок.

В зависимости от числа и устройства опор балки число реакций, подлежащих определению, бывает различно. Опоры балок по их устройству могут быть разделены на следующие три основных типа:

1) Шарнирно-неподвижная опора. Такая опора не даёт концу балки возможности передвигаться в каком-либо направлении, позволяя ему только поворачиваться относительно центра шарнира О. Неизвестную по величине и направлению реакцию R всегда можно заменить двумя составляющими: вертикальной R у по оси Oy и горизонтальной R x по оси Ox.

2) Шарнирно-подвижная опора. Такая опора отличается от шарнирно неподвижной тем, что у неё опорная подушка поставлена на катки, дающие возможность передвигаться концу балки вдоль оси по опорной плоскости. Направление опорной реакции всегда перпендикулярно к оси балки.

3) Жёстко защемляющая опора. Такая опора препятствует всякому перемещению конца балки в плоскости действия внешних нагрузок. И ещё препятствует вращению конца балки. Неизвестную реакцию R можно всегда заменить двумя составляющими: вертикальной R у по оси Oy и горизонтальной R х по оси Ox. И ещё неизвестный реактивный момент М R , препятствующий повороту балки.

В практике при изгибе чаще всего силы действуют перпендикулярно к продольной оси балки. В этих случаях число неизвестных реакций, возникающих на опорах, уменьшается, так как реакция по оси Ox в шарнирно неподвижной опоре и жёстко защемляющей опоре становится равной 0.

Определение опорных реакций балок.

В случае действия на балку сил, лежащих в одной плоскости, статика даёт три уравнения равновесия:

– сумма проекций всех сил, приложенных к балке, вместе с

Реакциями опор на оси Ox и Oy равны 0.

– сумма моментов всех сил должная быть равна 0.

В случае действия сил перпендикулярно оси Ox уравнение обращается в тождество.

Поперечная сила и изгибающий момент.

Для определения численного значения и направления поперечной силы и изгибающего момента применяют метод сечений. Для этого нужно мысленно разрезать балку сечением перпендикулярным к горизонтальной оси, отстоящем на расстоянии x от конца балки. Отбросив ту часть балки, где действует больше нагрузок, рассматривают равновесие оставшейся части. Все внешние силы, действующие на оставшуюся часть балки, могут быть заменены парой сил и силой, действующей в сечении.

Момент М пары внутренних сил , действующий в сечении, численно равный алгебраической сумме моментов всех внешних сил, действующих на оставшуюся часть балки, называется изгибающим моментом в сечении. Всегда направлен в положительном направлении, т. е. изгибает оставшуюся часть балки выпуклостью вниз. Т. е. если часть балки левая, то вращает оставшуюся часть балки против часовой стрелки. Если часть балки правая, то вращает по часовой стрелке.

Сила Q – результирующая внутренних сил, действующая в сечении, численно равная алгебраической сумме всех внешних сил, приложенных к оставшейся части балки, называется поперечной или перерезывающей силой в сечении. Поперечную силу будем считать положительной для левой части, если она действует вниз. Для правой части считается положительной действие поперечной силы вверх.

Изгиб бруса, производимый двумя равными моментами, направленными в противоположные стороны, называется чистым изгибом. В поперечной сечении возникает только один внутренний силовой фактор – .

Волокна, расположенные вдоль по длине балки, растягиваются по одной стороне; по другой – сжимаются. Вследствие удлинения одних волокон на выпуклой стороне и укорочения других на вогнутой стороне, вызываемых в брусе изгибающими моментами, в поперечных сечениях бруса возникают нормальные напряжения растяжения и сжатия (направлены перпендикулярно сечению). На границе между растянутым и сжатым слоем – нейтральный слой, волокна которого не растягиваются и не сжимаются, проходящий через центр тяжести сечения.

Поперечным изгибом называется изгиб бруса, при котором в поперечном сечении возникает два внутренних силовых фактора: Q – поперечная или перерезывающая сила, – изгибающий момент. Поперечные силы вызывают касательные напряжения.

При чистом и при поперечном изгибе плоские поперечные сечения остаются плоскими и после деформации. Плоские сечения взаимно поворачиваются одно относительно другого.

В случае чистого изгиба строят эпюру изгибающего момента.

В сечении, где имеет максимальное значение, вычисляют нормальное напряжение. Это значение напряжения сравнивают с допускаемым и делают вывод: прочность обеспечена или не обеспечена.

В случае поперечного изгиба строят эпюру изгибающего момента и перерезывающей силы. По максимальному изгибающему моменту рассчитывают нормальное напряжение.

По максимальной перерезывающей силе рассчитывают касательное напряжение. С помощью нормального и касательного напряжения находят эквивалентное нормальное по гипотезе прочности. Эквивалентное значение напряжения сравнивают с допускаемым. Делают вывод об обеспечении прочности.

Для наглядности изменения нагрузок по длине балки строят эпюры поперечной силы Q и изгибающего момента .

Правила построения эпюр:

Балку разбивают на участки. Проводят вниз вертикальные линии в точках приложения сосредоточенных сил и сосредоточенных моментов. Нумерация участков слева направо, если балка на двух и более опорах. Если балка со свободным концом (жесткая заделка – консоль), нумерацию следует выполнять со свободной стороны.

1. Ниже проводят две базовые нулевые линии для построения эпюры поперечной силы Q и изгибающего момента .

2. Положительные значения поперечной силы и изгибающего момента откладываются вверх от нулевой линии, отрицательные – вниз.

Для проверки правильности нахождения опорных реакций и определения внутренних силовых факторов Q и , исходя из условия равновесия для оставшейся части балки, выполняют анализ эпюр.

Анализ правильности построения эпюр:

1. На участке, где нет равномерно-распределённой нагрузки, эпюра поперечной силы представляет собой прямую, параллельную нулевой оси. Эпюра изгибаюшего момента представляет собой наклонную прямую. В точке, где приложена сосредоточенная сила, на эпюре поперечной силы должен быть скачок, равный по величине сосредоточенной силе. На эпюре изгибающего момента изменяется угол наклона.

2. Если на участке есть равномерно-распределённая нагрузка, то эпюра поперечной силы представляет собой наклонную прямую. Эпюра изгибающего момента будет параболой. При действии равномерно-распределённой нагрузки вниз, значение поперечной силы на эпюре будет убывать. Эпюра изгибающего момента будет параболой выпуклостью вверх. В точке пересечении поперечной силой нулевой линии и смене знака с плюса на минус на эпюре изгибающего момента будет максимум. При действии равномерно-распределённой нагрузки вверх, значение поперечной силы на эпюре будет возрастать. Эпюра изгибающего момента будет параболой вогнутостью вниз. В точке пересечения нулевой линии и смене знака с минуса на плюс на эпюре изгибающего момента будет минимум.

3. В точке, где приложен сосредоточенный момент, на эпюре изгибающего момента должен быть скачок, равный по величине сосредоточенному моменту. На эпюре поперечной силы изменений нет.

4. При изгибе справедливы дифференциальные зависимости: - интенсивность равномерно-распределённой нагрузки рана первой производной от поперечной силы (тангенс угла наклона эпюры поперечной силы) и второй производной от изгибающего момента. Поперечная сила равна первой производной от изгибающего момента и равна тангенсу угла наклона касательной к кривой изгибающего момента

Примеры построения простейших эпюр.

Пример 1: Консоль нагружена сосредоточенным моментом, построить эпюры поперечной силы и изгибающего момента.

Эпюра поперечной силы представляет собой нулевую линию.

Эпюра изгибающего момента представляет собой линию, параллельную нулевой оси. Решение: Проведем сечение на расстоянии х от свободного, незакреплённого конца. Поперечная или перерезывающей силы так как по условию равновесия отсечённой части поперечная сила равна сумме внешних сил, действующих на отсечённую часть. Внешних сил, приложенных к конструкции нет.

Положительное направление изгибающего момента , принадлежащего сечению считается направление по часовой. Изгибающий момент должен нижние волокна растягивать, верхние сжимать. В уравнении равновесия для отсечённой части он будет взят со знаком минус.

От нулевой линии откладываем вниз.

Пример 2: Консоль нагружена сосредоточенной силой, построить эпюры поперечной силы и изгибающего момента.Решение: Проведем сечение на расстоянии х от свободного, незакреплённого конца. Выберем положительное направление поперечной перерезывающей силы и изгибающего момента . Положительным считается направление поперечной силы вверх. Так как она должна разворачивать отсечённую часть по часовой стрелке. Вычисляем значение изгибающего момента в граничных точках участка при х=0 и при х=l.

Строим эпюры поперечной силы и изгибающего момента.

Для наглядного представления характера деформации брусьев (стержней) при изгибе проводится следующий опыт. На боковые грани резинового бруса прямоугольного сечения наносится сетка линий, параллельных и перпендикулярных оси бруса (рис. 30.7, а). Затем к брусу по его концам прикладываются моменты (рис. 30.7, б), действующие в плоскости симметрии бруса, пересекающей каждое его поперечное сечение по одной из главных центральных осей инерции. Плоскость, проходящая через ось бруса и одну из главных центральных осей инерции каждого его поперечного сечения, будем называть главной плоскостью.

Под действием моментов брус испытывает прямой чистый изгиб. В результате деформации, как показывает опыт, линии сетки, параллельные оси бруса, искривляются, сохраняя между собой прежние расстояния. При указанном на рис. 30.7, б направлении моментов эти линии в верхний части бруса удлиняются, а в нижней - укорачиваются.

Каждую линию сетки, перпендикулярную к оси бруса, можно рассматривать как след плоскости некоторого поперечного сечения бруса. Так как эти линии остаются прямыми, то можно предполагать, что поперечные сечения бруса, плоские до деформации, остаются плоскими и в процессе деформации.

Это предположение, основанное на опыте, как известно, носит название гипотезы плоских сечений, или гипотезы Бернулли (см. § 6.1).

Гипотеза плоских сечений применяется не только при чистом, но и при поперечном изгибе. Для поперечного изгиба она является приближенной, а для чистого изгиба строгой, что подтверждается теоретическими исследованиями, проведенными методами теории упругости.

Рассмотрим теперь прямой брус с поперечным сечением, симметричным относительно вертикальной оси, заделанный правым концом и нагруженный на левом конце внешним моментом действующим в одной из главных плоскостей бруса (рис. 31.7). В каждом поперечном сечении этого бруса возникают только изгибающие моменты действующие в той же плоскости, что и момент

Таким образом, брус на всем своем протяжении находится в состоянии прямого чистого изгиба. В состоянии чистого изгиба могут находиться отдельные участки балки и в случае действия на нее поперечных нагрузок; например, чистый изгиб испытывает участок 11 балки, изображенной на рис. 32.7; в сечениях этого участка поперечная сила

Выделим из рассматриваемого бруса (см. рис. 31.7) двумя поперечными сечениями элемент длиной . В результате деформации, как это следует из гипотезы Бернулли, сечения останутся плоскими, но наклонятся по отношению друг к другу на некоторый угол Примем левое сечение условно за неподвижное. Тогда в результате поворота правого сечения на угол оно займет положение (рис. 33.7).

Прямые пересекутся в некоторой точке А, которая является центром кривизны (или, точнее, следом оси кривизны) продольных волокон элемента Верхние волокна рассматриваемого элемента при показанном на рис. 31.7 направлении момента удлиняются, а нижние укорачиваются. Волокна же некоторого промежуточного слоя перпендикулярного к плоскости действия момента сохраняют свою длину. Этот слой называется нейтральным слоем.

Обозначим радиус кривизны нейтрального слоя, т. е. расстояние от этого слоя до центра кривизны А (см. рис. 33.7). Рассмотрим некоторый слой расположенный на расстоянии у от нейтрального слоя. Абсолютное удлинение волокон этого слоя равно а относительное

Рассматривая подобные треугольники устанавливаем, что Следовательно,

В теории изгиба предполагается, что продольные волокна бруса не давят друг на друга. Экспериментальные и теоретические исследования показывают, что это предположение не влияет существенно на результаты расчета.

При чистом изгибе в поперечных сечениях бруса не возникают касательные напряжения. Таким образом, все волокна при чистом изгибе находятся в условиях одноосного растяжения или сжатия.

По закону Гука для случая одноосного растяжения или сжатия нормальное напряжение о и соответствующая относительная деформация связаны зависимостью

или на основании формулы (11.7)

Из формулы (12.7) следует, что нормальные напряжения в продольных волокнах бруса прямо пропорциональны их расстояниям у от нейтрального слоя. Следовательно, в поперечном сечении бруса в каждой его точке нормальные напряжения пропорциональны расстоянию у от этой точки до нейтральной оси, представляющей собой линию пересечения нейтрального слоя с поперечным сечением (рис.

34.7, а). Из симметрии бруса и нагрузки следует, что нейтральная ось горизонтальна.

В точках нейтральной оси нормальные напряжения равны нулю; по одну сторону от нейтральной оси они растягивающие, а по другую - сжимающие.

Эпюра напряжений о представляет собой график, ограниченный прямой линией, с наибольшими по абсолютной величине значениями напряжений для точек, наиболее удаленных от нейтральной оси (рис. 34.7,б).

Рассмотрим теперь условия равновесия выделенного элемента бруса. Действие левой части бруса на сечение элемента (см. рис. 31.7) представим в виде изгибающего момента остальные внутренние усилия в этом сечении при чистом изгибе равны нулю. Действие правой части бруса на сечение элемента представим в виде элементарных сил о приложенных к каждой элементарной площадке поперечного сечения (рис. 35.7) и параллельных оси бруса.

Составим шесть условий равновесия элемента

Здесь - суммы проекций всех сил, действующих на элемент соответственно на оси - суммы моментов всех сил относительно осей (рис. 35.7).

Ось совпадает с нейтральной осью сечения а ось у перпендикулярна к ней; обе эти оси расположены в плоскости поперечного сечения

Элементарная сила не дает проекций на оси у и и не вызывает момента относительно оси Поэтому уравнения равновесия удовлетворяются при любых значениях о.

Уравнение равновесия имеет вид

Подставим в уравнение (13.7) значение а по формуле (12.7):

Так как (рассматривается изогнутый элемент бруса, для которого ), то

Интеграл представляет собой статический момент поперечного сечения бруса относительно нейтральной оси . Равенство его нулю означает, что нейтральная ось (т. е. ось ) проходит через центр тяжести поперечного сечения. Таким образом, центр тяжести всех поперечных сечений бруса, а следовательно, и ось бруса, являющаяся геометрическим местом центров тяжести, расположены в нейтральном слое. Следовательно, радиус кривизны нейтрального слоя является радиусом кривизны изогнутой оси бруса.

Составим теперь уравнение равновесия в виде суммы моментов всех сил, приложенных к элементу бруса, относительно нейтральной оси :

Здесь представляет собой момент элементарной внутренней силы относительно оси .

Обозначим площадь части поперечного сечения бруса, расположенной над нейтральной осью, - под нейтральной осью.

Тогда представит собой равнодействующую элементарных сил приложенных выше нейтральной оси, ниже нейтральной оси (рис. 36.7).

Обе эти равнодействующие равны друг другу по абсолютной величине, так как их алгебраическая сумма на основании условия (13.7) равна нулю. Эти равнодействующие образуют внутреннюю пару сил, действующую в поперечном сечении бруса. Момент этой пары сил, равный т. е. произведению величины одной из них на расстояние между ними (рис. 36.7), представляет собой изгибающий момент в поперечном сечении бруса.

Подставим в уравнение (15.7) значение а по формуле (12.7):

Здесь представляет собой осевой момент инерции , т. е. оси, проходящей через центр тяжести сечения. Следовательно,

Подставим значение из формулы (16.7) в формулу (12.7):

При выводе формулы (17.7) не учтено, что при внешнем моменте направленном, как это показано на рис. 31.7, согласно принятому правилу знаков, изгибающий момент является отрицательным. Если учесть это, то перед правой частью формулы (17.7) необходимо поставить знак «минус». Тогда при положительном изгибающем моменте в верхней зоне бруса (т. е. при ) значения а получатся отрицательными, что укажет на наличие в этой зоне сжимающих напряжений. Однако обычно знак «минус» в правой части формулы (17.7) не ставится, а эта, формула используется лишь для определения абсолютных значений напряжений а. Поэтому в формулу (17.7) следует подставлять абсолютные значения изгибающего момента и ординаты у. Знак же напряжений всегда легко устанавливается по знаку момента или по характеру деформации балки.

Составим теперь уравнение равновесия в виде суммы моментов всех сил, приложенных к элементу бруса, относительно оси у:

Здесь представляет собой момент элементарной внутренней силы относительно оси у (см. рис. 35.7).

Подставим в выражение (18.7) значение а по формуле (12.7):

Здесь интеграл представляет собой центробежный момент инерции поперечного сечения бруса относительно осей у и . Следовательно,

Но так как

Как известно (см. § 7.5), центробежный момент инерции сечения равен нулю относительно главных осей инерции.

В рассматриваемом случае ось у является осью симметрии поперечного сечения бруса и, следовательно, оси у и являются главными центральными осями инерции этого сечения. Поэтому условие (19.7) здесь удовлетворяется.

В случае, когда поперечное сечение изгибаемого бруса не имеет ни одной оси симметрии, условие (19.7) удовлетворяется, если плоскость действия изгибающего момента проходит через одну из главных центральных осей инерции сечения или параллельна этой оси.

Если плоскость действия изгибающего момента не проходит ни через одну из главных центральных осей инерции поперечного сечения бруса и не параллельна ей, то условие (19.7) не удовлетворяется и, следовательно, нет прямого изгиба - брус испытывает косой изгиб.

Формула (17.7), определяющая нормальное напряжение в произвольной точке рассматриваемого сечения бруса, применима при условии, что плоскость действия изгибающего момента проходит через одну из главных осей инерции этого сечения или ей параллельна. При этом нейтральная ось поперечного сечения является его главной центральной осью инерции, перпендикулярной к плоскости действия изгибающего момента.

Формула (16.7) показывает, что при прямом чистом изгибе кривизна изогнутой оси бруса прямо пропорциональна произведению модуля упругости Е на момент инерции Произведение будем называть жесткостью сечения при изгибе; она выражается в и т. д.

При чистом изгибе балки постоянного сечения изгибающие моменты и жесткости сечений постоянны по ее длине. В этом случае радиус кривизны изогнутой оси балки имеет постоянное значение [см. выражение (16.7)], т. е. балка изгибается по дуге окружности.

Из формулы (17.7) следует, что наибольшие (положительные - растягивающие) и наименьшие (отрицательные-сжимающие) нормальные напряжения в поперечном сечении бруса возникают в точках, наиболее удаленных от нейтральной оси, расположенных по обе стороны от нее. При поперечном сечении, симметричном относительно нейтральной оси, абсолютные величины наибольших растягивающих и сжимающих напряжений одинаковы и их можно определить по формуле

где - расстояние от нейтральной оси до наиболее удаленной точки сечения.

Величина зависящая только от размеров и формы поперечного сечения, называется осевым моментом сопротивления сечения и обозначается

(20.7)

Следовательно,

Определим осевые моменты сопротивления для прямоугольного и круглого сечений.

Для прямоугольного сечения шириной b и высотой

Для круглого сечения диаметром d

Момент сопротивления выражается в .

Для сечений, не симметричных относительно нейтральной оси, например для треугольника, тавра и т. п., расстояния от нейтральной оси до наиболее удаленных растянутых и сжатых волокон различны; поэтому для таких сечений имеются два момента сопротивления:

где - расстояния от нейтральной оси до наиболее удаленных растянутых и сжатых волокон.

Деформация изгиба заключается в искривлении оси прямого стержня или в изменении начальной кривизны прямого стержня (рис. 6.1). Ознакомимся с основными понятиями, которые используются при рассмотрении деформации изгиба.

Стержни, работающие на изгиб, называют балками .

Чистым называется изгиб, при котором изгибающий момент является единственным внутренним силовым фактором, возникающем в поперечном сечении балки.

Чаще, в поперечном сечении стержня наряду с изгибающим моментом возникает также и поперечная сила. Такой изгиб называют поперечным.

Плоским (прямым) называют изгиб, когда плоскость действия изгибающего момента в поперечном сечении проходит через одну из главных центральных осей поперечного сечения.

При косом изгибе плоскость действия изгибающего момента пересекает поперечное сечение балки по линии, не совпадающей ни с одной из главных центральных осей поперечного сечения.

Изучение деформации изгиба начнем со случая чистого плоского изгиба.

Нормальные напряжения и деформации при чистом изгибе.

Как уже было сказано, при чистом плоском изгибе в поперечном сечении из шести внутренних силовых факторов не равен нулю только изгибающий момент (рис. 6.1, в):

Опыты, поставленные на эластичных моделях, показывают, что если на поверхность модели нанести сетку линий (рис. 6.1, а), то при чистом изгибе она деформируется следующим образом (рис. 6.1, б):

а) продольные линии искривляются по длине окружности;

б) контуры поперечных сечений остаются плоскими;

в) линии контуров сечений всюду пересекаются с продольными волокнами под прямым углом.

На основании этого можно предположить, что при чистом изгибе поперечные сечения балки остаются плоскими и поворачиваются так, что остаются нормальными к изогнутой оси балки (гипотеза плоских сечений при изгибе).

Рис. 6.1

Замеряя длину продольных линий (рис. 6.1, б), можно обнаружить, что верхние волокна при деформации изгиба балки удлиняются, а нижние укорачиваются. Очевидно, что можно найти такие волокна, длина которых остается неизменной. Совокупность волокон, не меняющих своей длины при изгибе балки, называется нейтральным слоем (н. с.) . Нейтральный слой пересекает поперечное сечение балки по прямой, которая называетсянейтральной линией (н. л.) сечения .

Для вывода формулы, определяющей величину нормальных напряжений, возникающих в поперечном сечении, рассмотрим участок балки в деформированном и не деформированном состоянии (рис. 6.2).

Рис. 6.2

Двумя бесконечно малыми поперечными сечениями выделим элемент длиной

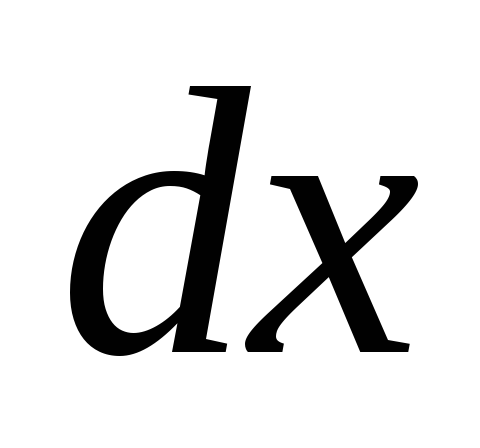. До деформации сечения, ограничивающие элемент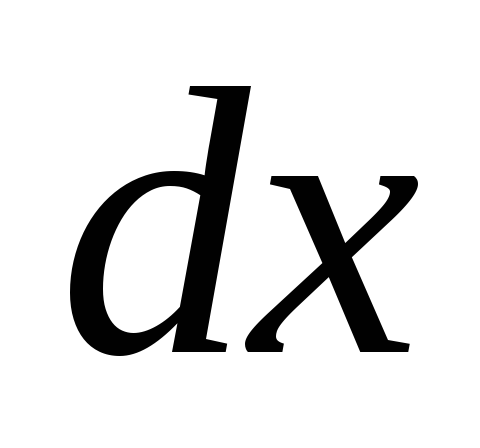

, были параллельны между собой (рис. 6.2, а), а после деформации они несколько наклонились, образуя угол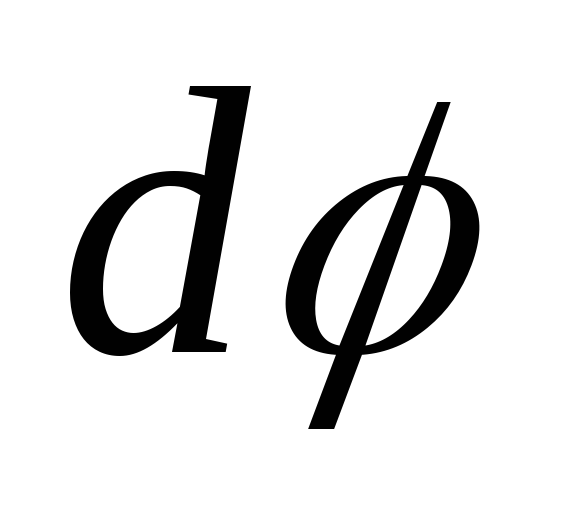

. Длина волокон, лежащих в нейтральном слое, при изгибе не меняется

. Обозначим радиус кривизны следа нейтрального слоя на плоскости чертежа буквой. Определим линейную деформацию произвольного волокна

, отстоящего на расстоянииот нейтрального слоя.

Длина этого волокна после деформации (длина дуги

) равна

. Учитывая, что до деформации все волокна имели одинаковую длину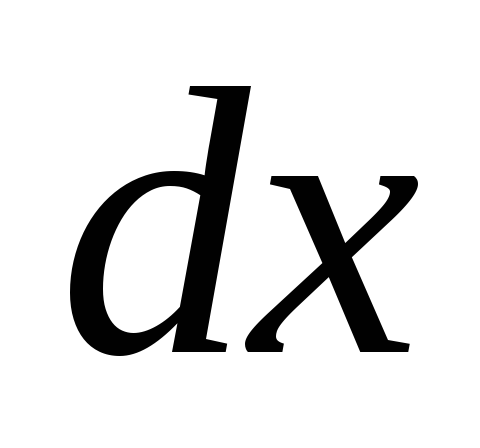

, получим, что абсолютное удлинение рассматриваемого волокна

Его относительная деформация

Очевидно, что

, так как длина волокна, лежащего в нейтральном слое не изменилась. Тогда после подстановки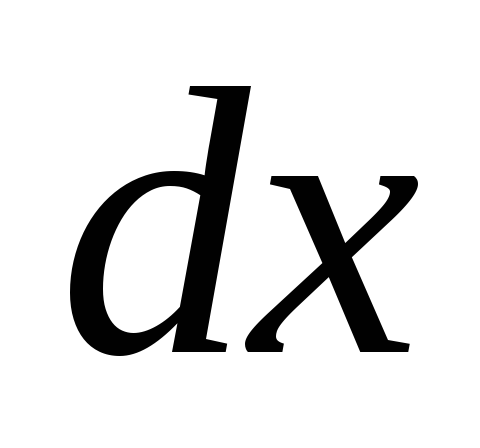

получим

(6.2)

Следовательно, относительная продольная деформация пропорциональна расстоянию волокна от нейтральной оси.

Введем предположение, что при изгибе продольные волокна не надавливают друг на друга. При таком предположении каждое волокно деформируется изолировано, испытывая простое растяжение или сжатие, при котором

. С учетом (6.2)

, (6.3)

т. е. нормальные напряжения прямо пропорциональны расстояниям рассматриваемых точек сечения от нейтральной оси.

Подставим зависимость (6.3) в выражение изгибающего момента

в поперечном сечении (6.1)

Вспомним, что интеграл

представляет собой момент инерции сечения относительно оси

(6.4)

Зависимость (6.4) представляет собой закон Гука при изгибе, поскольку она связывает деформацию (кривизну нейтрального слоя

) с действующим в сечении моментом. Произведение

носит название жесткости сечения при изгибе, Н·м 2 .

Подставим (6.4) в (6.3)

(6.5)

Это и есть искомая формула для определения нормальных напряжений при чистом изгибе балки в любой точке ее сечения.

Для того, чтобы установить, где в поперечном сечении находится нейтральная линия подставим значение нормальных напряжений в выражение продольной силы

и изгибающего момента